A particle moves with an initial velocity V0 and retardation αv , where α is a constant and v is the velocity at any time t.
total distance covered by the particle is
u/k
uk
uk
u2k
The correct Answer is:A
To solve the problem of finding the total distance covered by a particle moving with an initial velocity V0 and a retardation proportional to its velocity, we can follow these steps:
Step 1: Understand the Retardation
The problem states that the particle has a retardation given by αv, where α is a constant and v is the velocity at any time t. This means that the acceleration a can be expressed as:
a=−αv
Step 2: Relate Acceleration to Velocity
Using the definition of acceleration, we can write:
a=dvdt
Thus, we have:
dvdt=−αv
Step 3: Separate Variables and Integrate
We can separate the variables to integrate:
dvv=−αdt
Now, we integrate both sides. The limits for v will be from V0 to v and for t from 0 to t:
∫vV01vdv=−α∫t0dt
This gives:
lnv−lnV0=−αt
Simplifying, we find:
ln(vV0)=−αt
Exponentiating both sides, we obtain:
v=V0e−αt
Step 4: Relate Velocity to Distance
The velocity v is also defined as the rate of change of displacement s:
v=dsdt
Substituting the expression for v:
dsdt=V0e−αt
Step 5: Integrate to Find Distance
Now, we can integrate to find the total distance s:
ds=V0e−αtdt
Integrating both sides, we have:
s=∫t0V0e−αtdt
The integral of e−αt is:
s=V0(−1αe−αt)t0
Evaluating this gives:
s=−V0α(e−αt−1)=V0α(1−e−αt)
Step 6: Find Total Distance as t→∞
To find the total distance covered by the particle, we take the limit as t approaches infinity:
s=V0α(1−e−αt)as t→∞
As t→∞, e−αt→0:
s=V0α(1−0)=V0α
Final Answer
The total distance covered by the particle is:
V0α
The problem states that the particle has a retardation given by αv, where α is a constant and v is the velocity at any time t. This means that the acceleration a can be expressed as:
a=−αv
Using the definition of acceleration, we can write:
a=dvdt
Thus, we have:
dvdt=−αv
We can separate the variables to integrate:
dvv=−αdt
Now, we integrate both sides. The limits for v will be from V0 to v and for t from 0 to t:
∫vV01vdv=−α∫t0dt
This gives:
lnv−lnV0=−αt
Simplifying, we find:
ln(vV0)=−αt
Exponentiating both sides, we obtain:
v=V0e−αt
The velocity v is also defined as the rate of change of displacement s:
v=dsdt
Substituting the expression for v:
dsdt=V0e−αt
Now, we can integrate to find the total distance s:
ds=V0e−αtdt
Integrating both sides, we have:
s=∫t0V0e−αtdt
The integral of e−αt is:
s=V0(−1αe−αt)t0
Evaluating this gives:
s=−V0α(e−αt−1)=V0α(1−e−αt)
To find the total distance covered by the particle, we take the limit as t approaches infinity:
s=V0α(1−e−αt)as t→∞
As t→∞, e−αt→0:
s=V0α(1−0)=V0α
The total distance covered by the particle is:
V0α
Similar Questions
A particle moves with an initial velocity V0 and retardation αv , where α is a constant and v is the velocity at any time t.
Velocity of particle at time is :
View SolutionA particle moves with an initial velocity V0 and retardation αv , where α is a constant and v is the velocity at any time t.
After how much time, speed of particle decreases by 75%
View SolutionA particle moves with initial velocity v0 and retardation αv, where v is velocity at any instant t. Then the particle
View SolutionA particle moves with an initial v0 and retardation alphav, where v is its velocity at any time t.
(i) The particle will cover a total distance v0α.
(ii) The particle will come to rest after time 1α.
(iii) The particle will continue to move for a very long time.
(iv) The velocity of the particle will become v02 after time 1n2α
View SolutionA particle moving in the positive x-direction has initial velocity v0. The particle undergoes retardation kv2 , where vis its instantaneous velocity. The velocity of the particle as a function of time is given by:
View SolutionA point moves in a straight line under the retardation av2, where 'a' is a positive constant and v is speed. If the initial speed is u, the distance covered in 't' seconds is :
View SolutionA particle having a velocity v=v0 at t=0 is decelerated at the rate |a|=α√v, where α is a positive constant.
View SolutionThe retardation of a particle moving in a straight line is proportional to its displacement proportionallity constant being unity. Find the total distance convered by the particle till it comes to rest. Given that velocity of particle is v0 at zero displacement.
View SolutionRefering to v−s diagram, find:
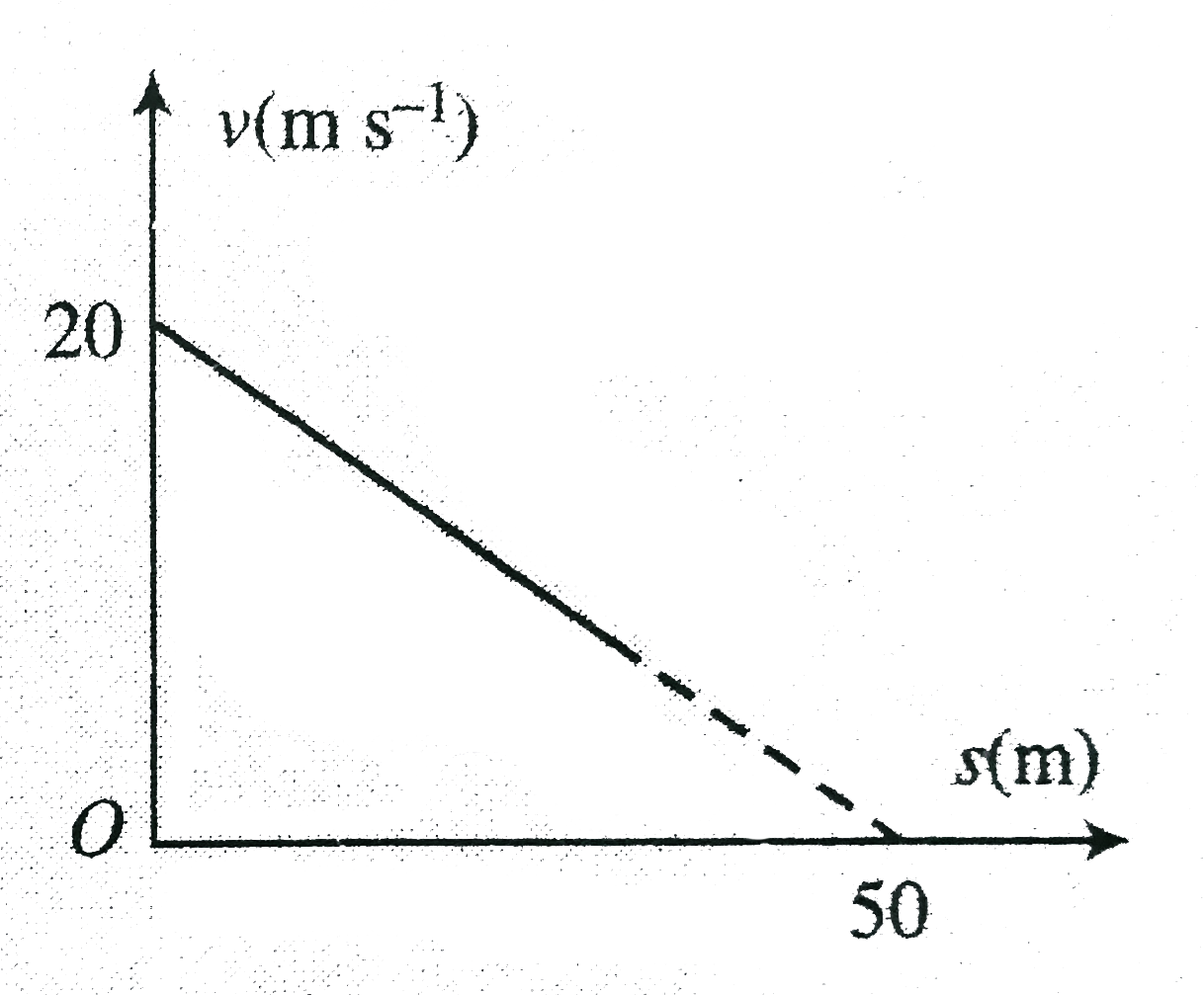 .
.
a. Acceleration of the particle when its velocity becomes half of the initial velocity.
b. Total distance covered by the particle.
View SolutionA point moves rectilinearly with deceleration whose modulus depends on the velocity v of the particle as α=k√v, where k is a positive constant. At the initial moment the velocity of the point is equal to V0. What distance will it take to cover that distance?
View Solution
