A particle moving in the positive x-direction has initial velocity v0. The particle undergoes retardation kv2 , where vis its instantaneous velocity. The velocity of the particle as a function of time is given by:
v=v0/(1+kv0t)
v=2v01+kt
v=v0kt
v=v0(1+k2v02t)
The correct Answer is:A
To find the velocity of a particle moving in the positive x-direction with an initial velocity v0 and undergoing a retardation of kv2, we can follow these steps:
Step 1: Set up the equation for retardation
The retardation is given by −kv2. According to Newton's second law, we can express this as:
dvdt=−kv2
Step 2: Rearrange the equation
We can rearrange the equation to separate the variables:
dvv2=−kdt
Step 3: Integrate both sides
Now, we will integrate both sides. The left side integrates to:
∫dvv2=−1v
And the right side integrates to:
∫−kdt=−kt+C
where C is the constant of integration.
Step 4: Combine the results of the integration
Combining the results from the integration gives us:
−1v=−kt+C
Step 5: Solve for the constant of integration
To find the constant C, we use the initial condition. At t=0, v=v0:
−1v0=C
Thus, we can substitute C back into our equation:
−1v=−kt−1v0
Step 6: Rearrange to find v
Rearranging the equation gives:
1v=kt+1v0
Taking the reciprocal of both sides, we find:
v=v01+kv0t
Final Result
Thus, the velocity of the particle as a function of time is:
v(t)=v01+kv0t
---
The retardation is given by −kv2. According to Newton's second law, we can express this as:
dvdt=−kv2
We can rearrange the equation to separate the variables:
dvv2=−kdt
Now, we will integrate both sides. The left side integrates to:
∫dvv2=−1v
And the right side integrates to:
∫−kdt=−kt+C
where C is the constant of integration.
Combining the results from the integration gives us:
−1v=−kt+C
To find the constant C, we use the initial condition. At t=0, v=v0:
−1v0=C
Thus, we can substitute C back into our equation:
−1v=−kt−1v0
Rearranging the equation gives:
1v=kt+1v0
Taking the reciprocal of both sides, we find:
v=v01+kv0t
Thus, the velocity of the particle as a function of time is:
v(t)=v01+kv0t
Similar Questions
A particle moves with an initial velocity V0 and retardation αv , where α is a constant and v is the velocity at any time t.
Velocity of particle at time is :
View SolutionA particle moves with initial velocity v0 and retardation αv, where v is velocity at any instant t. Then the particle
View Solution
Knowledge Check
A particle moves in a plane with a constant acceleration in a direction different from the initial velocity. The path of the particle is
Astraight lineBarc of circleCparabolaDellipse
A particle moves with an initial velocity V0 and retardation αv , where α is a constant and v is the velocity at any time t.
After how much time, speed of particle decreases by 75%
View SolutionA particle moves with an initial velocity V0 and retardation αv , where α is a constant and v is the velocity at any time t.
total distance covered by the particle is
View SolutionA particle of unit mass is moving along x-axis. The velocity of particle varies with position x as v(x). =αx−β (where α and β are positive constants and x>0 ). The acceleration of the particle as a function of x is given as
View SolutionThe position- time graph of a moving particle is shown. The instantaneous velocity of the particle is negative at the point
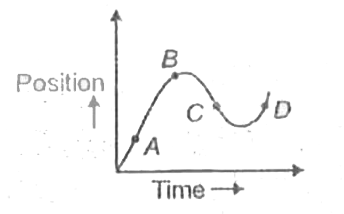
View SolutionA particle is moving with constant speed v along x - axis in positive direction. Find the angular velocity of the particle about the point (0, b), when position of the particle is (a, 0).
View SolutionA particle of unit mass undergoes one-dimensional motion such that its velocity varies according to
v(x)=βx−2n
where β and n are constant and x is the position of the particle. The acceleration of the particle as a function of x is given by.
View SolutionA particle of unit mass undergoes one-dimensional motion such that its velocity varies according to
v(x)=βx−2n
where β and n are constant and x is the position of the particle. The acceleration of the particle as a function of x is given by.
View Solution
