Two bodies are projected from the same point with equal velocities in such a directions that they strike on the same point on a plane whose inclination is β. If α is the angle of projection of the first , the ratio of there times of flight is
sin(α−β):cosα
cosα:sin(α−β)
sin(α+β):cosα
cosα:sin(α+β)
The correct Answer is:A
To solve the problem, we need to find the ratio of the times of flight of two bodies projected from the same point with equal velocities, striking the same point on an inclined plane.
1. Understanding the Problem:
- We have two bodies projected from the same point with equal initial velocities u.
- The first body is projected at an angle α with respect to the horizontal, and the second body is projected at an angle α′.
- Both bodies strike the same point on an inclined plane that is inclined at an angle β.
2. Using the Range Formula:
- The range R of a projectile on an inclined plane can be expressed as:
R=u2gcos2β(sin(2α−β)−sin(β))
- For both projectiles to reach the same point, their ranges must be equal:
u2gcos2β(sin(2α−β)−sin(β))=u2gcos2β(sin(2α′−β)−sin(β))
3. Cancelling Common Terms:
- Since u2gcos2β is common on both sides, we can cancel it out:
sin(2α−β)−sin(β)=sin(2α′−β)−sin(β)
- This simplifies to:
sin(2α−β)=sin(2α′−β)
4. Using the Sine Function Property:
- From the property of the sine function, we know:
sinA=sinB⟹A=B or A=π−B
- Thus, we have two cases:
- Case 1: 2α−β=2α′−β (which leads to α=α′, not useful here)
- Case 2: 2α−β=π−(2α′−β)
5. Solving for α′:
- Rearranging Case 2 gives:
2α+2α′=π+2β
2α′=π−2α−2β
α′=π2−α−β
6. Finding Time of Flight:
- The time of flight T for the first body is given by:
T=2usin(α−β)gcos(β)
- The time of flight T′ for the second body is:
T′=2usin(α′−β)gcos(β)
7. Finding the Ratio of Times of Flight:
- The ratio TT′ becomes:
TT′=sin(α−β)sin(α′−β)
- Substituting α′=π2−α−β:
TT′=sin(α−β)sin(π2−α−β−β)=sin(α−β)cos(α)
8. Final Result:
- Therefore, the ratio of the times of flight is:
TT′=sin(α−β)cos(α)
- We have two bodies projected from the same point with equal initial velocities u.
- The first body is projected at an angle α with respect to the horizontal, and the second body is projected at an angle α′.
- Both bodies strike the same point on an inclined plane that is inclined at an angle β.
- The range R of a projectile on an inclined plane can be expressed as:
R=u2gcos2β(sin(2α−β)−sin(β))
- For both projectiles to reach the same point, their ranges must be equal:
u2gcos2β(sin(2α−β)−sin(β))=u2gcos2β(sin(2α′−β)−sin(β))
- Since u2gcos2β is common on both sides, we can cancel it out:
sin(2α−β)−sin(β)=sin(2α′−β)−sin(β)
- This simplifies to:
sin(2α−β)=sin(2α′−β)
- From the property of the sine function, we know:
sinA=sinB⟹A=B or A=π−B
- Thus, we have two cases:
- Case 1: 2α−β=2α′−β (which leads to α=α′, not useful here)
- Case 2: 2α−β=π−(2α′−β)
- Rearranging Case 2 gives:
2α+2α′=π+2β
2α′=π−2α−2β
α′=π2−α−β
- The time of flight T for the first body is given by:
T=2usin(α−β)gcos(β)
- The time of flight T′ for the second body is:
T′=2usin(α′−β)gcos(β)
- The ratio TT′ becomes:
TT′=sin(α−β)sin(α′−β)
- Substituting α′=π2−α−β:
TT′=sin(α−β)sin(π2−α−β−β)=sin(α−β)cos(α)
- Therefore, the ratio of the times of flight is:
TT′=sin(α−β)cos(α)
Similar Questions
Two bodies are projected from the same point with equal speeds in such directions that they both strike the same point on a plane whose inclination is β. If α the angle of projection of the first body with the horizontal , show that the ratio of their time of flights is sin(α−β)cosα
View SolutionTwo particle are projected with same initial velocities at an angle 30∘ and 60∘ with the horizontal .Then
View SolutionTwo balls are projected from the same point with such a speed that both reach the same point on ground at a distance of 19.6√3m from the point of projection. If one of the particles is projected at an angle of 30∘ with the ground, then calculate the time of flight of the second ball.
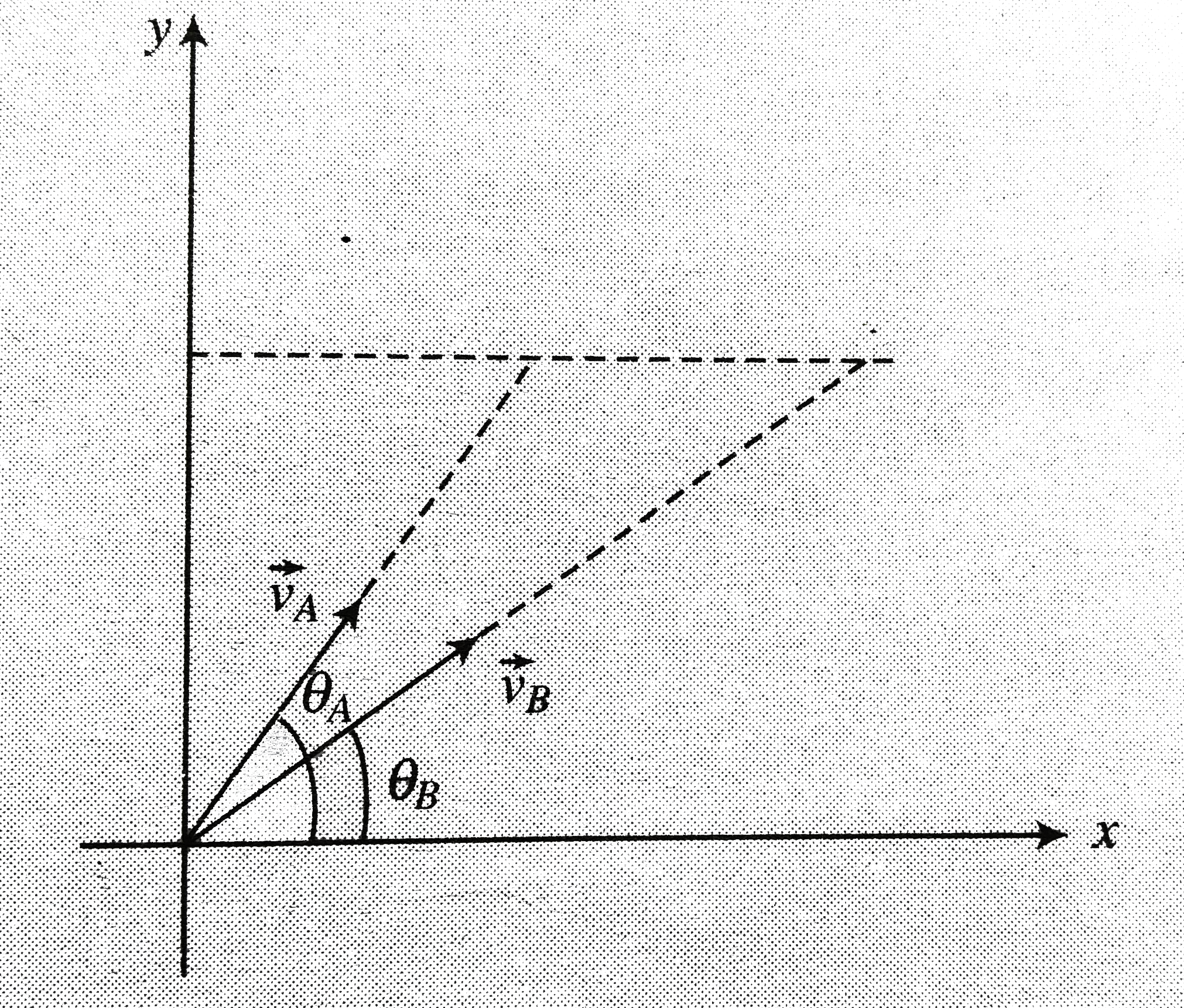
View SolutionTwo particles A and B are projected from the same point in different direction in such a manner that their velocity vectors are shown in the diagram :−
 .
.
View SolutionTwo balls are projected from the same point in the direction inclined at 60∘ and 30∘ to the horizontal. If they attain the same height , what is the ratio of their velocities ? What is the ratio of their initial velocities if they have same horizontal range ?
View SolutionTwo particles are projected from the same point with the same speed at different angles θ1 & θ2 to the horizontal. They have the same range. Their times of flight are t1 & t2 respectily
View SolutionThe objects x and y are projected from a point with same velocities , at angle 30∘and60∘, the ratio of their maximum height attained:
View SolutionTwo particles AandB are projected from the same point in different directions in such a manner that vertical components of their initial velocities are same (Fig. 5.8). Find the ratio of range.
 .
.
View SolutionTwo particles projected form the same point with same speed u at angles of projection αandβ strike the horizontal ground at the same point. If h1andh2 are the maximum heights attained by the projectile, R is the range for both and t1andt2 are their times of flights, respectively, then incorrect option is :
View SolutionTwo particles projected form the same point with same speed u at angles of projection αandβ strike the horizontal ground at the same point. If h1andh2 are the maximum heights attained by the projectile, R is the range for both and t1andt2 are their times of flights, respectively, then
View Solution
