A particle is projected horizontally with a speed v0 at t = 0 from a certain point above the ground . What is the magnitude of tangential acceleration of the particle at t=t1 is ( Assume that the particle does not strike the ground between the time interval t = 0 to t=t1 )
gt√v20+g2+2
tg2√v20+g2t2
tg√v20+g2t2
gt√g+v20t
The correct Answer is:B
To solve the problem of finding the magnitude of tangential acceleration of a particle projected horizontally with speed v0 at t=0, we can follow these steps:
Step 1: Understand the Motion
The particle is projected horizontally, meaning its initial vertical velocity Vy0=0. The only force acting on the particle in the vertical direction is gravity, which causes a downward acceleration of g.
Step 2: Determine the Vertical Velocity at Time t1
The vertical velocity Vy at time t1 can be calculated using the equation of motion:
Vy=Vy0+ay⋅t
Since Vy0=0 and ay=g (downward), we have:
Vy=0+g⋅t1=gt1
Step 3: Determine the Angle of the Velocity Vector
At time t1, the horizontal velocity Vx remains constant and equal to v0. The vertical velocity is Vy=gt1. The angle θ of the resultant velocity vector can be found using the tangent function:
tanθ=VyVx=gt1v0
Step 4: Calculate sinθ
To find sinθ, we can use the relationship:
sinθ=Vy√V2x+V2y=gt1√v20+(gt1)2
Step 5: Determine the Tangential Acceleration
The tangential acceleration at is given by:
at=gsinθ
Substituting for sinθ:
at=g⋅gt1√v20+(gt1)2=g2t1√v20+(gt1)2
Final Result
Thus, the magnitude of the tangential acceleration of the particle at time t1 is:
at=g2t1√v20+(gt1)2
The particle is projected horizontally, meaning its initial vertical velocity Vy0=0. The only force acting on the particle in the vertical direction is gravity, which causes a downward acceleration of g.
The vertical velocity Vy at time t1 can be calculated using the equation of motion:
Vy=Vy0+ay⋅t
Since Vy0=0 and ay=g (downward), we have:
Vy=0+g⋅t1=gt1
At time t1, the horizontal velocity Vx remains constant and equal to v0. The vertical velocity is Vy=gt1. The angle θ of the resultant velocity vector can be found using the tangent function:
tanθ=VyVx=gt1v0
To find sinθ, we can use the relationship:
sinθ=Vy√V2x+V2y=gt1√v20+(gt1)2
The tangential acceleration at is given by:
at=gsinθ
Substituting for sinθ:
at=g⋅gt1√v20+(gt1)2=g2t1√v20+(gt1)2
Thus, the magnitude of the tangential acceleration of the particle at time t1 is:
at=g2t1√v20+(gt1)2
Similar Questions
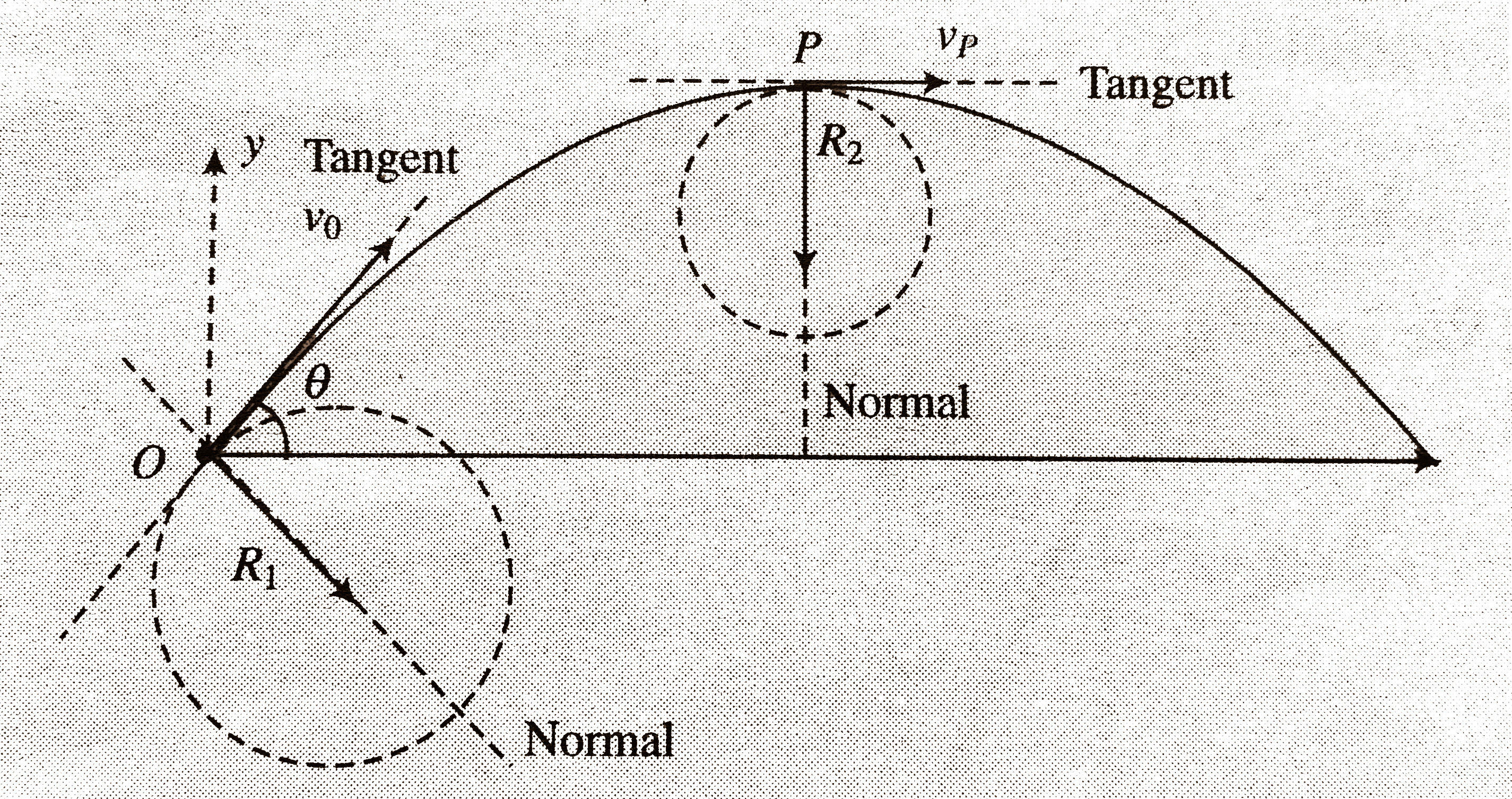
A particle is projected at angle θ with horizontal with velocity v0att=0. Find
(a) tangential and normal acceleration of the particle at t=0 and at highest point of its trajectory.
(b) the radius of curvature a=0 and highest point.
 .
.
View SolutionA particle is projected at t=0 with velocity u at angle θ with the horizontal. Then the ratio of the tangential acceleration and the radius of curvature at the point of projection is :
View Solution
Knowledge Check
A particle is projected at time t=0 from a point P on the ground with a speed v0, at an angle of 45∘ to the horizontal. Find the magnitude and direction of the angular momentum of the particle about P at tiem t=v0/g
Aa. mv302√2gBb. mv30√2gCc. 3mv30√2gDd. √2mv30g
A particle is projected at time t=0 from a point P wilth a speed v0 at an angle of 45∘ to the horizontal. Find the magnitude and the direction of the angular momentum of the particle about the point P at time t=v0g
View SolutionA particle is projected from ground with speed 80 m/s at an angle 30∘ with horizontal from ground. The magnitude of average velocity of particle in time interval t = 2 s to t = 6 s is [Take g = 10 m/s2]
View SolutionA particle is projected with a speed v and an angle θ to the horizontal. After a time t, the magnitude of the instantaneous velocity is equal to the magnitude of the average velocity from 0 to t. Find t.
View SolutionA particle is moving with speed v=b√x along positive x-axis. Calculate the speed of the particle at time t=τ (assume tha the particle is at origin at t= 0).
View SolutionA starts from rest, with uniform acceleration a. The acceleration of the body as function of time t is given by the equation a = pt, where p is a constant, then the displacement of the particle in the time interval t = 0 to t=t1 will be
View SolutionA particle moves vertically with an upwards initial speed v0=10.5ms−1. If its acceleration varies with time as shown in a-t graph in figure, find the velocity of the particles at t = 4s.

View SolutionA particle moves according to the law x=rcos(pi)t/(2) The distance covered by it in the time interval between t=0 to t=3s is
View Solution
