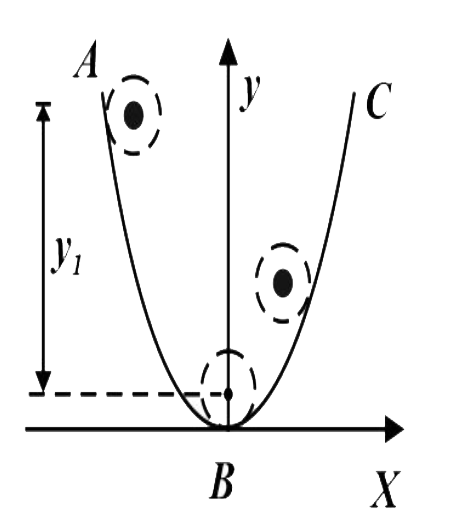
A solid sphere rolls down a parabolic path , whose vertical dimension is given by y=kx2 and base of the parabola is at x = 0 . During the fall the sphere does not slip, but beyond the base the climb is frictionless. If the sphere falls through a height h, the height above the base that it would climb is
54
7h
75h
57h
The correct Answer is:D
To solve the problem of a solid sphere rolling down a parabolic path and then climbing back up, we can follow these steps:
Step 1: Understand the Energy Conservation
When the sphere rolls down the parabolic path, it converts potential energy into kinetic energy. The potential energy lost by the sphere when it falls through a height h is given by:
PE=mgh
Step 2: Calculate the Kinetic Energy
The kinetic energy of the sphere at the bottom of the parabolic path consists of both translational and rotational kinetic energy. The total kinetic energy KE can be expressed as:
KE=KEtranslational+KErotational=12mv2+12Iω2
For a solid sphere, the moment of inertia I is given by I=25mr2 and the relationship between linear velocity v and angular velocity ω is v=rω. Thus, we can substitute ω:
KE=12mv2+12(25mr2)(v2r2)=12mv2+15mv2=710mv2
Step 3: Apply Energy Conservation
By the principle of conservation of energy, the potential energy lost equals the kinetic energy gained:
mgh=710mv2
We can cancel m from both sides (assuming m≠0):
gh=710v2
Step 4: Solve for v2
Rearranging the equation gives:
v2=107gh
Step 5: Analyze the Climb
When the sphere climbs back up, it will convert its kinetic energy back into potential energy. The kinetic energy at the base is:
KE=710mv2=710m(107gh)=mgh
As the sphere climbs, it will reach a maximum height h0 where all the kinetic energy is converted into potential energy:
mgh=mgh0
Thus, we can write:
h0=h
Step 6: Find the Height Above the Base
However, since the sphere rolls down a height h and then climbs back up, we need to consider the energy loss due to the climb. The energy available for climbing is:
KE=mgh−mgh0
Setting the kinetic energy equal to the potential energy at height h0:
mgh0=710mgh
Cancelling m gives:
h0=710h
Final Result
The height above the base that the sphere would climb is:
h0=57h
When the sphere rolls down the parabolic path, it converts potential energy into kinetic energy. The potential energy lost by the sphere when it falls through a height h is given by:
PE=mgh
The kinetic energy of the sphere at the bottom of the parabolic path consists of both translational and rotational kinetic energy. The total kinetic energy KE can be expressed as:
KE=KEtranslational+KErotational=12mv2+12Iω2
For a solid sphere, the moment of inertia I is given by I=25mr2 and the relationship between linear velocity v and angular velocity ω is v=rω. Thus, we can substitute ω:
KE=12mv2+12(25mr2)(v2r2)=12mv2+15mv2=710mv2
By the principle of conservation of energy, the potential energy lost equals the kinetic energy gained:
mgh=710mv2
We can cancel m from both sides (assuming m≠0):
gh=710v2
Rearranging the equation gives:
v2=107gh
When the sphere climbs back up, it will convert its kinetic energy back into potential energy. The kinetic energy at the base is:
KE=710mv2=710m(107gh)=mgh
As the sphere climbs, it will reach a maximum height h0 where all the kinetic energy is converted into potential energy:
mgh=mgh0
Thus, we can write:
h0=h
However, since the sphere rolls down a height h and then climbs back up, we need to consider the energy loss due to the climb. The energy available for climbing is:
KE=mgh−mgh0
Setting the kinetic energy equal to the potential energy at height h0:
mgh0=710mgh
Cancelling m gives:
h0=710h
The height above the base that the sphere would climb is:
h0=57h
Similar Questions
A uniform cylinder rolls down from rest, on a track whose vertical cross - section is a parabola given by the equation y=kx2. If the surface is rough from A to B due to which the cylinder doesn't slip but it is frictionless from B to C, then the height of ascent of cylinder towards C is
View Solution
A solid ball rolls down a parabolic path ABC from a height h as shown in figure. Portion AB of the path is rough while BC is smooth. How high will the ball climb in BC?
View SolutionThe radius of the base of a cone and the radius of a sphere are the same, each being 8 cm. Given that the volumes of these two solids are also the same, calculate the slant height of the cone.
View SolutionA hollow spherical ball rolls down on a parabolic path AB from a height 'h' as shown in the figure. Path AB is rough enough to prevent slipping of ball and path BC is frictionless. The height to which the ball will climb in BC is

View SolutionA solid sphere of radius r is melted and cast into the shape of a solid cone of height r , the radius of the base of the cone is
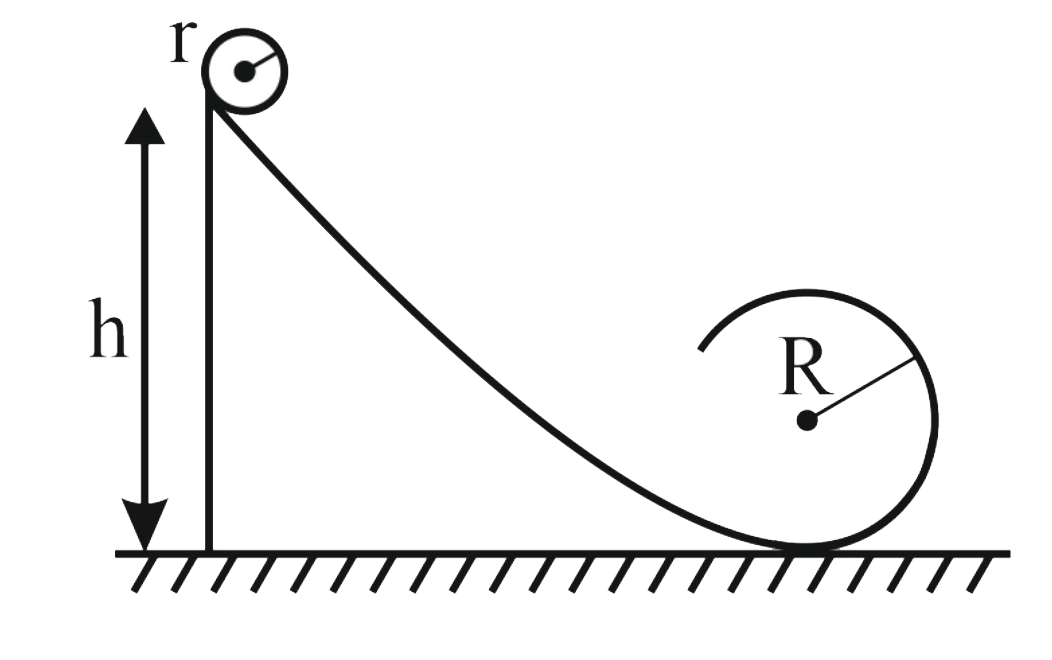
View SolutionA solid sphere rolls without slipping along the track shown in the figure. The sphere starts from rest from a height h above the bottom of the loop of radius R which is much larger than the radius of the sphere r. The minimum value of h for the sphere to complete the loop is
View SolutionA solid sphere of radius r is melted and cast into the shape of a solid cone of height r , the radius of the base of the cone is (a) 2r (b) 3r (c) r (d) 4r
View Solution
A solid sphere of mass ma nd radis R is placed on a rough horizontal surface A horizontal force F is applied to sphere at a height h, (0≤h≤R) from centre. If sphere rolls slipping then,
View SolutionTwo small insulating spheres are attached to silk threads. The spheres have equal masses of 40g and have electric charges of q1=+2.0μC and q2=−2.0μC. The spheres are brought into the initial positions shown in Figure(a), with a vertical separation of 15cm between them. In figure, the upper thread is slowly pulled upward, while point B is kept fixed. When point a has been raised through a height h, the lower sphere suddenly falls, as shown in Figure (b). The height h, is closest to:
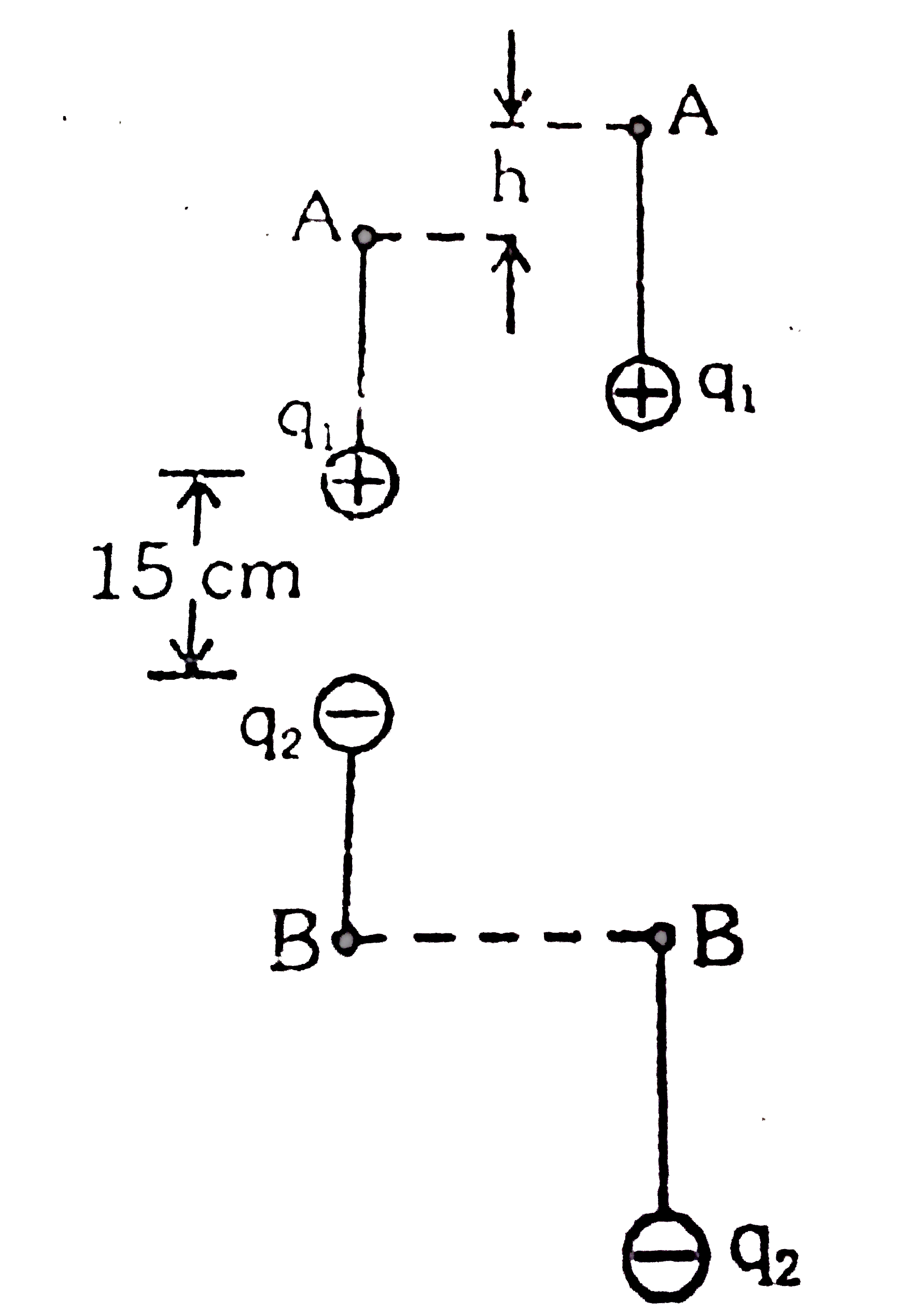
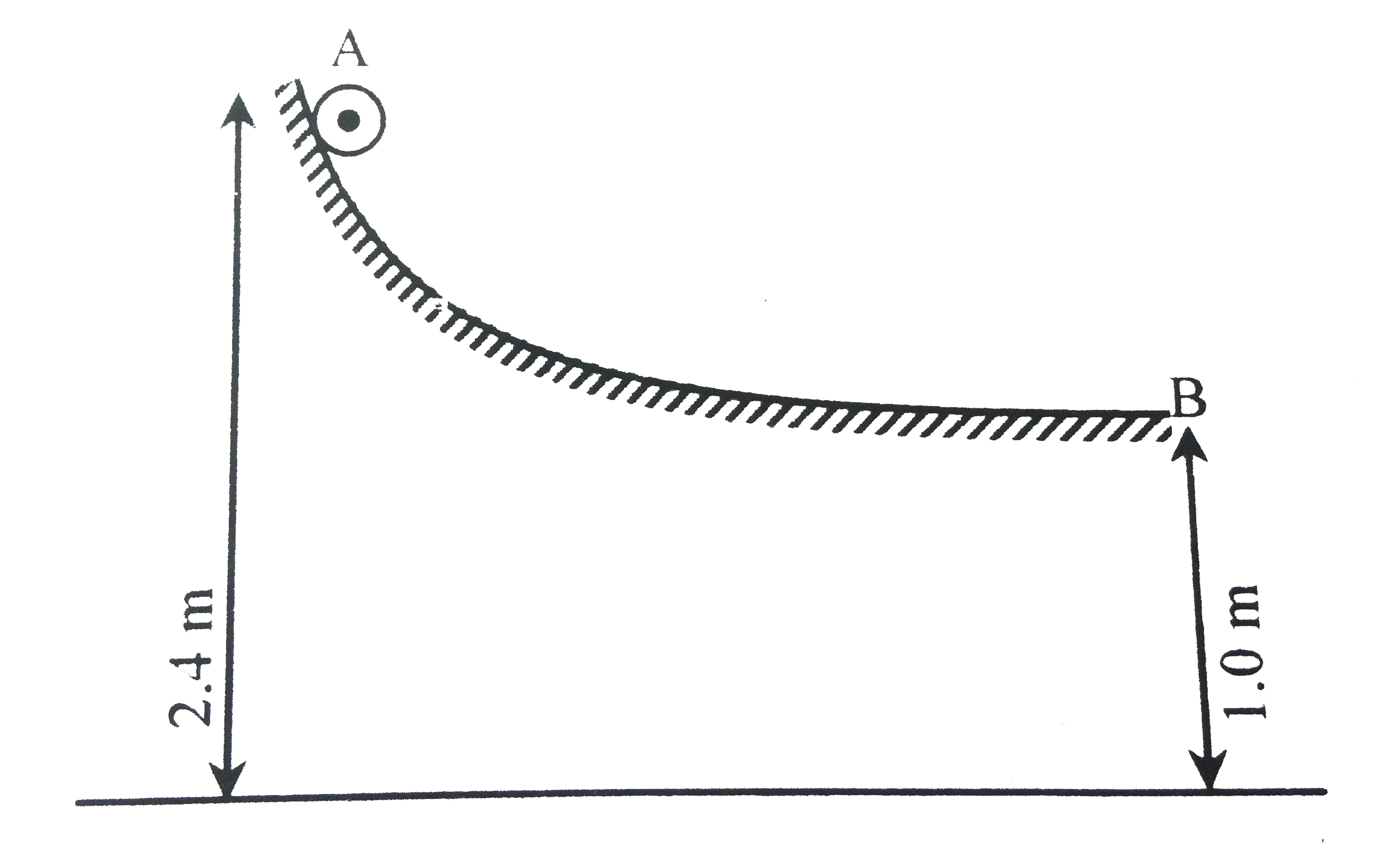
View SolutionA small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part. The horizontall part is 1.0 meter above the ground level and the top of the track is 2.4 meter above the ground. Find the distance on the ground with respect to a point B( which is vetically below the end A of the track as shown in fig.) where the sphere lands.
 .
.
(A) 1m
(B) 2m
( C) 3m
(D) 4m.
View Solution
