A hollow spherical ball rolls down on a parabolic path AB from a height 'h' as shown in the figure. Path AB is rough enough to prevent slipping of ball and path BC is frictionless. The height to which the ball will climb in BC is

h
h2
3h5
5h7
Step by step video & image solution for A hollow spherical ball rolls down on a parabolic path AB from a height 'h' as shown in the figure. Path AB is rough enough to prevent slipping of ball and path BC is frictionless. The height to which the ball will climb in BC is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - C) Objective Type Questions (More than one option are correct)
29 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - D) Linked Comprehension Type Questions
20 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - A) Objective Type Questions (One option is correct)
62 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions

A solid ball rolls down a parabolic path ABC from a height h as shown in figure. Portion AB of the path is rough while BC is smooth. How high will the ball climb in BC?
View SolutionA small spherical ball is released from a point at a height h on a rough track shown in figure. Assuming that it does not slip anywhere, find its linear speed when it rolls on the horizontal part of the track.

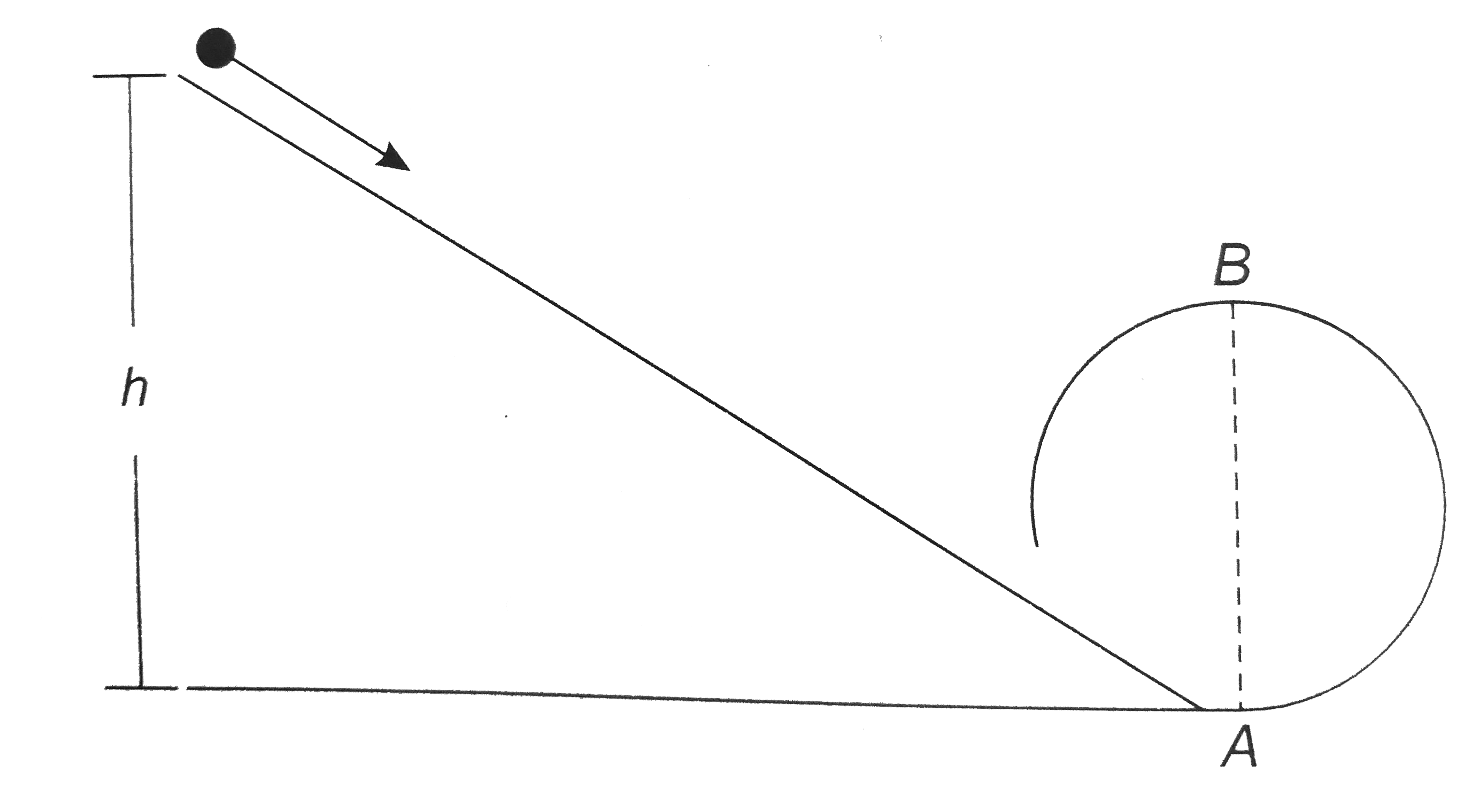
View SolutionA body initially rest and sliding along a frictionless trick from a height h (as shown in the figure) just completes a vertical circle of diameter AB=D. The height h is equal to
View SolutionA small metallic spherical ball is dropped from a height h. If it collides with the ground inelastically and rebounds, then
View SolutionA solid sphere rolls down a parabolic path , whose vertical dimension is given by y=kx2 and base of the parabola is at x = 0 . During the fall the sphere does not slip, but beyond the base the climb is frictionless. If the sphere falls through a height h, the height above the base that it would climb is
View SolutionA small disc of mass m is released at height h ,on a circular track of radius R, whose part AB has sufficient friction to prevent slipping ,while BC smooth. The maximum height attained by disc on BC is
View SolutionA uniform solid spherical ball is rolling down a smooth inclined plane from a height h. The velocity attained by the ball when it reaches the bottom of the inclined plane is v. If ball when it reaches the bottom of the inclined plane is v. If the ball is now thrown vertically upwards with the same velocity v, the maximum height to which the ball will rise is
View SolutionA smooth ball is released from rest from a height h as shown in figure. It slides down the first inclined plane and collides with the second inclined plane.
a. If e=0, find the speed of the ball just after leaving the inclined plane 1.
b. If the particle mioves horizontally just after the collision find e.

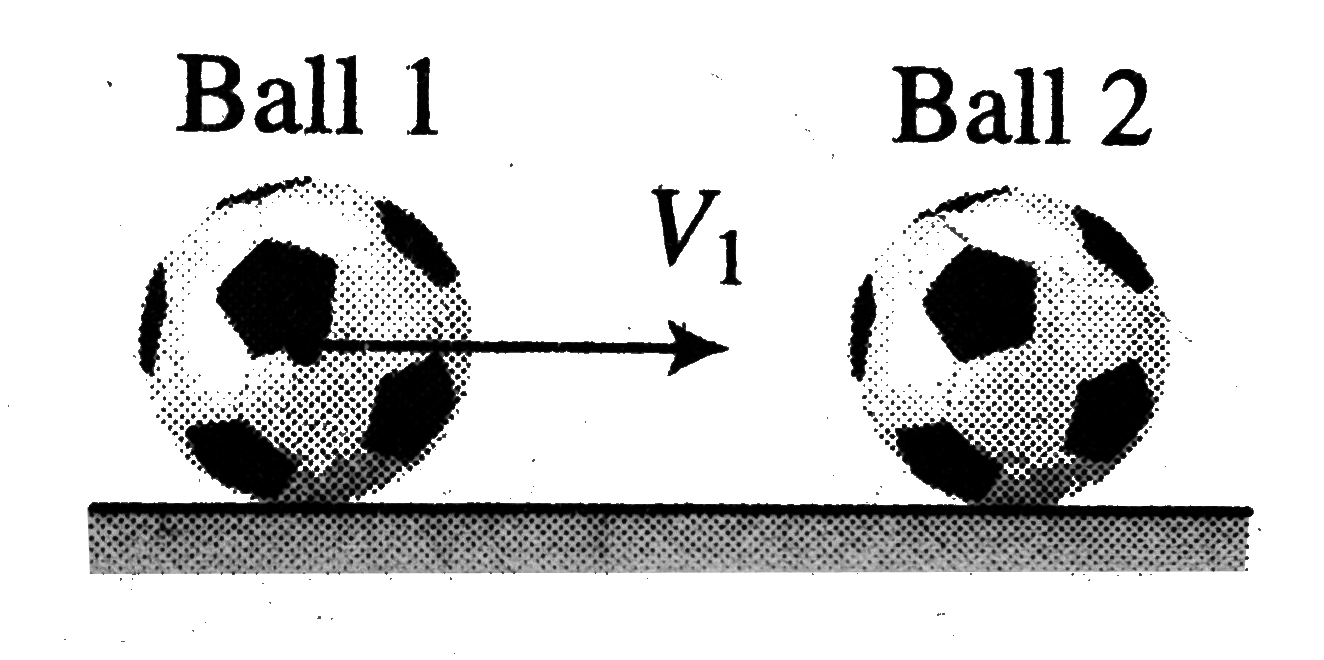
View SolutionA solid spherical ball rolling without slipping collides elastically with an identical ball at rest, as shown in the figure. Assuming that the frictional forces are small enough to have negligible effect during the instant of collision, calculate, the velocity of each ball along enough time after the collision when each ball is again rolling without slipping.
View SolutionA ball is projected upwards from a height h above the surface of the earth with velocity v. The time at which the ball strikes the ground is
View Solution
