A particle mass 1 kg is moving along a straight line y=x+4. Both x and y are in metres. Velocity of the particle is 2m/s. Find the magnitude of angular momentum of the particle about origin.
To find the magnitude of the angular momentum of a particle moving along the line y=x+4 about the origin, we can follow these steps:
Step 1: Identify the position of the particle
The line y=x+4 indicates that for any value of x, the corresponding y can be calculated. We can choose a specific point on this line. For simplicity, let's choose x=0:
y=0+4=4
Thus, at x=0, the position of the particle is (0,4).
Step 2: Determine the velocity vector
The particle is moving with a velocity of 2m/s. Since it is moving along the line y=x+4, we need to find the direction of this velocity. The slope of the line is 1 (since y=x+4), which means the direction vector can be represented as (1,1).
To convert this direction into a unit vector:
Magnitude of direction vector=√12+12=√2
Thus, the unit direction vector is:
^v=(1√2,1√2)
Now, the velocity vector →v can be calculated as:
→v=2⋅^v=2(1√2,1√2)=(√2,√2)m/s
Step 3: Calculate the angular momentum
The angular momentum →L of a particle about a point is given by:
→L=→r×→p
where →r is the position vector from the origin to the particle, and →p is the linear momentum of the particle.
The position vector →r is:
→r=(0,4)
The linear momentum →p is:
→p=m→v=1⋅(√2,√2)=(√2,√2)kg m/s
Step 4: Compute the cross product
The angular momentum →L can be computed using the determinant:
→L=→r×→p=∣∣
∣
∣∣^i^j^k040√2√20∣∣
∣
∣∣
Calculating this determinant, we find:
→L=^k(0⋅√2−4⋅√2)=−4√2^k
Thus, the magnitude of angular momentum is:
L=4√2kg m2/s
Final Answer
The magnitude of the angular momentum of the particle about the origin is:
L=4√2≈5.656kg m2/s
The line y=x+4 indicates that for any value of x, the corresponding y can be calculated. We can choose a specific point on this line. For simplicity, let's choose x=0:
y=0+4=4
Thus, at x=0, the position of the particle is (0,4).
The particle is moving with a velocity of 2m/s. Since it is moving along the line y=x+4, we need to find the direction of this velocity. The slope of the line is 1 (since y=x+4), which means the direction vector can be represented as (1,1).
Magnitude of direction vector=√12+12=√2
Thus, the unit direction vector is:
^v=(1√2,1√2)
Now, the velocity vector →v can be calculated as:
→v=2⋅^v=2(1√2,1√2)=(√2,√2)m/s
The angular momentum →L of a particle about a point is given by:
→L=→r×→p
where →r is the position vector from the origin to the particle, and →p is the linear momentum of the particle.
→r=(0,4)
The linear momentum →p is:
→p=m→v=1⋅(√2,√2)=(√2,√2)kg m/s
The angular momentum →L can be computed using the determinant:
→L=→r×→p=∣∣
∣
∣∣^i^j^k040√2√20∣∣
∣
∣∣
Calculating this determinant, we find:
→L=^k(0⋅√2−4⋅√2)=−4√2^k
Thus, the magnitude of angular momentum is:
L=4√2kg m2/s
The magnitude of the angular momentum of the particle about the origin is:
L=4√2≈5.656kg m2/s
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.64videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.72videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.411videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
A particle of mass 1 kg is moving along the line y=x+2 (here x and y are in metres) with speed 2m/s. The magnitude of angular momentum of paticle about origin is -
View SolutionA particle of mass m=3kg moves along a straight line 4y−3x=2 where x and y are in metre, with constant velocity v=5ms−1 the magnitude of angular momentum about the origin is
View SolutionA particle P is moving along a straight line as shown in the figure. During the motion of the particle from A to B the angular momentum of the particle about O
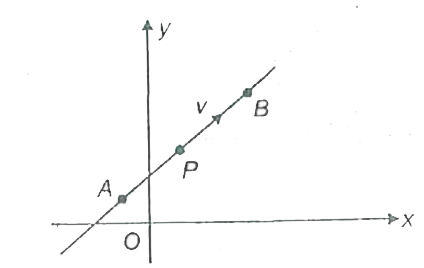 View Solution
View SolutionA particle of mass m is travelling with a constant velocity v=v0ˆi along the line y=b,z=0. Let dA be the area swept out by the position vector from origin to the particle in time dt and L the magnitude of angular momentum of particle about origin at any time t. Then
View SolutionThe velocity of a particle moving along x-axis is given as v=x2−5x+4 (in m/s) where x denotes the x-coordinate of the particle in metres. Find the magnitude of acceleration of the particle when the velocity of particle is zero?
View SolutionA body of mass 10 kg moves along a straight line y=x+5, where x and y are in metres with velocity 2 m/s. Its angular momentum about a point having co-ordinate (0,1) is
View SolutionA particle of mass m moves along line PC with velocity v as shown. What is the angular momentum of the particle about O?
 View Solution
View SolutionA particle is moving parallel to x-axis as shown in the figure. The angular velocity of the particle about the origin is
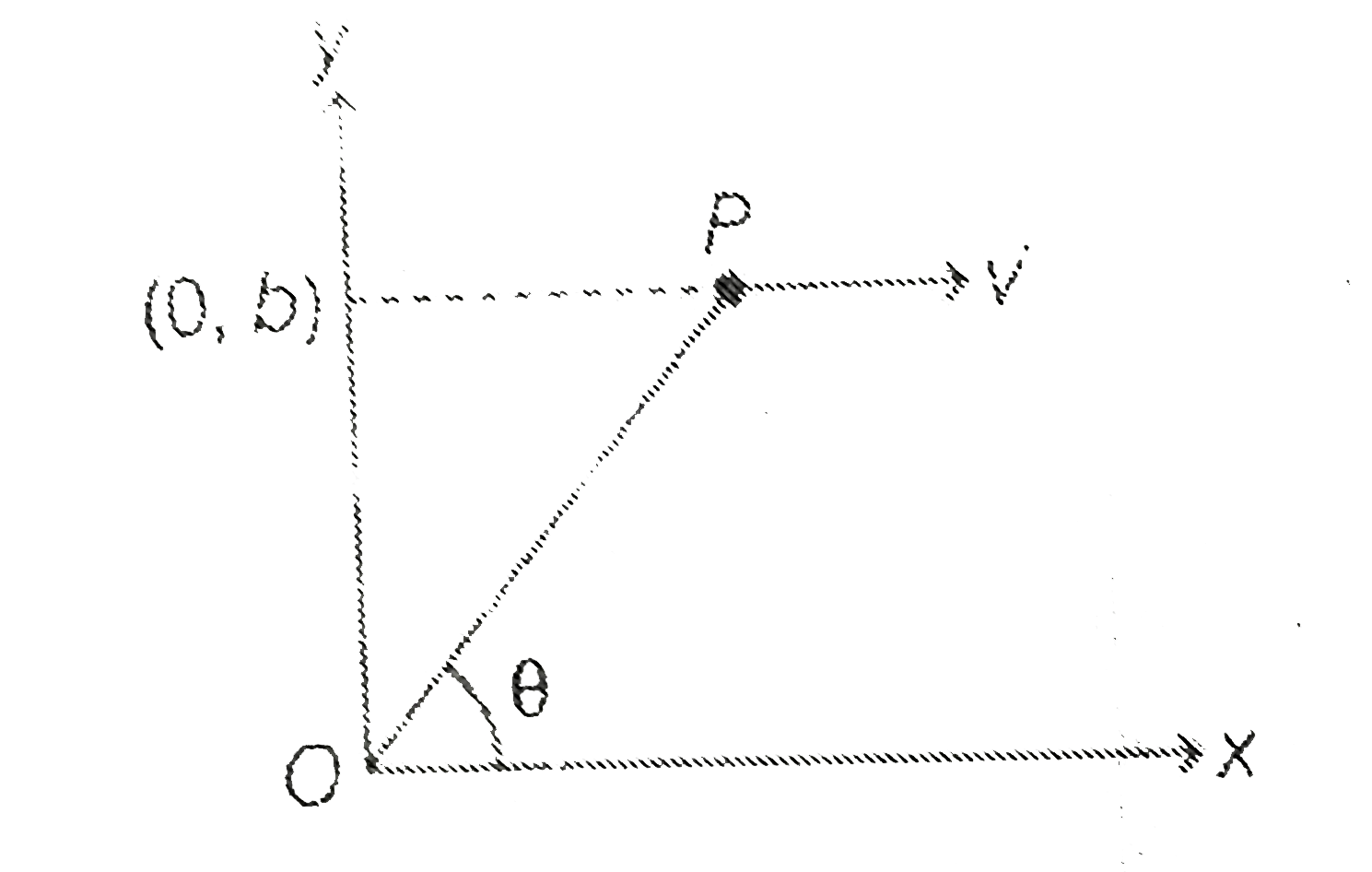 View Solution
View SolutionA particle moves in a straight line with a uniform acceleration a. Initial velocity of the particle is zero. Find the average velocity of the particle in first 's' distance.
View SolutionThe acceleration-displacement graph of a particle moving in a straight line is as shown in figure, initial velocity of particle is zero. Find the velocity of the particle when displacement of the particle is s=12m.
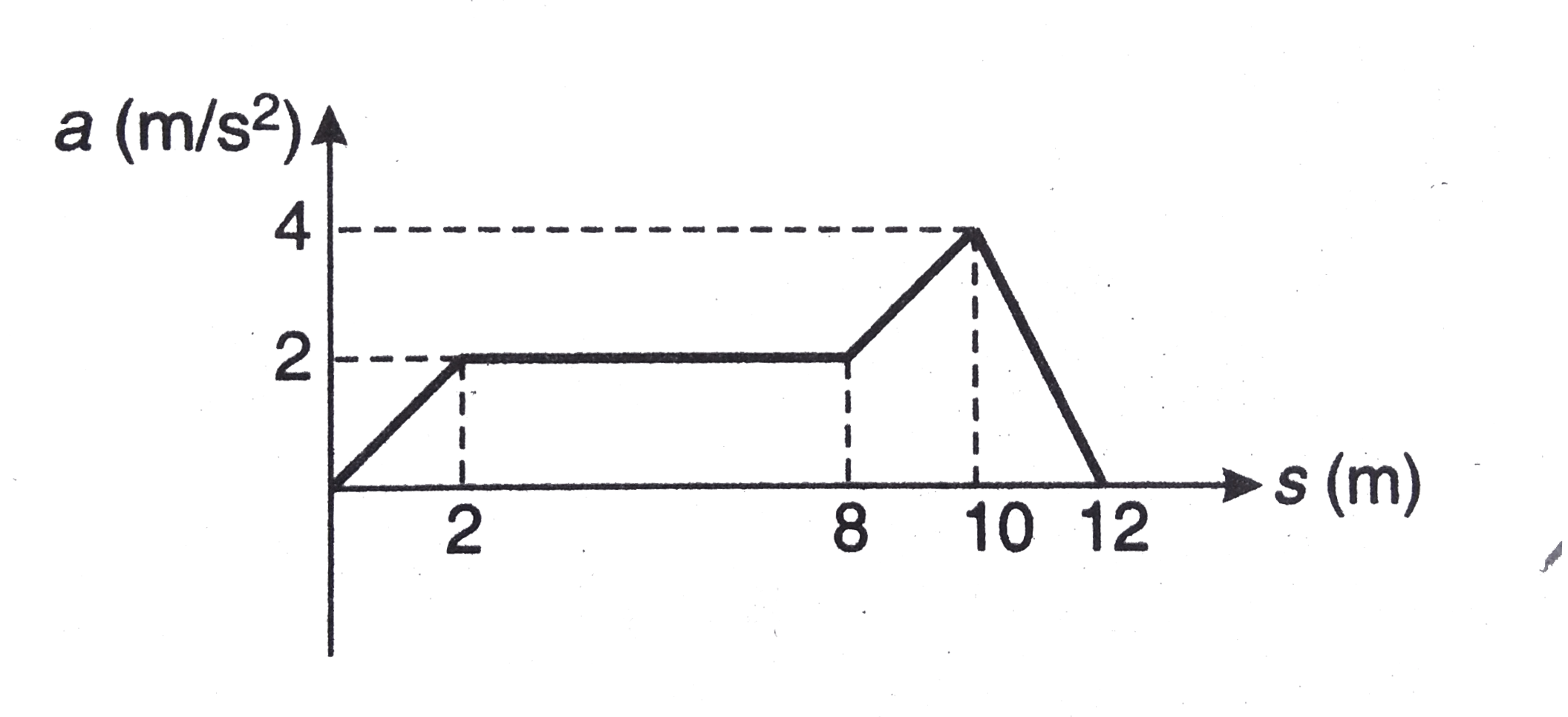 View Solution
View Solution

