Question

The moment of inertia of a semicircular ring of mass M and radius R about an axis which is passing through its centre and at an angle ${\displaystyle \theta }$ with the line joining its ends ( as shown ) is

Options

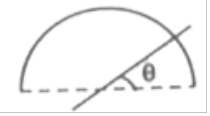
A. dependent on angle `theta`
B. independent of angle `theta`
C. `(MR^(2))/(2)` if `theta = 45^(@)`
D. `(MR^(2))/( 2) ` if `theta = 90^(@)`

Answer

B::C::D