The moment of inertia of a uniform semicircular wire of mass M and radius R about an axis passing through its centre of mass and perpendicular to its plane is xMR210. Find the value of x? (Take π2=10)
To find the value of x in the expression for the moment of inertia of a uniform semicircular wire, we can follow these steps:
Step 1: Understand the problem
We need to calculate the moment of inertia I of a semicircular wire of mass M and radius R about an axis passing through its center of mass and perpendicular to its plane.
Step 2: Identify the center of mass
The center of mass of a uniform semicircular wire lies along the axis of symmetry, at a distance d from the center of the semicircle. The distance d can be calculated as:
d=2Rπ
Step 3: Use the parallel axis theorem
According to the parallel axis theorem, the moment of inertia about an axis O (which is at the center of the semicircle) can be expressed as:
IO=ICM+Md2
where ICM is the moment of inertia about the center of mass and d is the distance from the center of mass to the axis at point O.
Step 4: Calculate the moment of inertia about the center of mass
The moment of inertia IO about the center of the semicircle can be calculated as:
IO=12MR2
This is the moment of inertia of a full circular wire, but since we have a semicircular wire, we take half of it.
Step 5: Substitute d into the equation
Substituting d into the parallel axis theorem gives:
IO=ICM+M(2Rπ)2
Substituting d:
IO=ICM+M⋅4R2π2
Step 6: Solve for ICM
Rearranging gives:
ICM=IO−M⋅4R2π2
Substituting IO=12MR2:
ICM=12MR2−M⋅4R2π2
Factoring out MR2:
ICM=MR2(12−4π2)
Step 7: Substitute π2=10
Now substituting π2=10:
ICM=MR2(12−410)
Calculating the expression:
ICM=MR2(12−25)=MR2(510−410)=MR2⋅110
Step 8: Relate to the given expression
The problem states that:
ICM=xMR210
Equating the two expressions gives:
MR2⋅110=xMR210
Step 9: Solve for x
Since MR2 and 10 can be cancelled from both sides:
1=x
Thus, the value of x is:
1
We need to calculate the moment of inertia I of a semicircular wire of mass M and radius R about an axis passing through its center of mass and perpendicular to its plane.
The center of mass of a uniform semicircular wire lies along the axis of symmetry, at a distance d from the center of the semicircle. The distance d can be calculated as:
d=2Rπ
According to the parallel axis theorem, the moment of inertia about an axis O (which is at the center of the semicircle) can be expressed as:
IO=ICM+Md2
where ICM is the moment of inertia about the center of mass and d is the distance from the center of mass to the axis at point O.
The moment of inertia IO about the center of the semicircle can be calculated as:
IO=12MR2
This is the moment of inertia of a full circular wire, but since we have a semicircular wire, we take half of it.
Substituting d into the parallel axis theorem gives:
IO=ICM+M(2Rπ)2
Substituting d:
IO=ICM+M⋅4R2π2
Rearranging gives:
ICM=IO−M⋅4R2π2
Substituting IO=12MR2:
ICM=12MR2−M⋅4R2π2
Factoring out MR2:
ICM=MR2(12−4π2)
Now substituting π2=10:
ICM=MR2(12−410)
Calculating the expression:
ICM=MR2(12−25)=MR2(510−410)=MR2⋅110
The problem states that:
ICM=xMR210
Equating the two expressions gives:
MR2⋅110=xMR210
Since MR2 and 10 can be cancelled from both sides:
1=x
Thus, the value of x is:
1
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - H) Multiple True-False Type Questions
4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - I) Subjective Type Questions
8 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - F) Matrix-Match Type Questions
8 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
The moment of inertia of a uniform semicircular wire of mass m and radius r, about an axis passing through its centre of mass and perpendicular to its plane is mr2(−kπ2). Find the value of k.
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionRadius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionThe moment of inertia of a circular ring of mass 1 kg about an axis passing through its centre and perpendicular to its plane is 4 kg m2. The diameter of the ring is
View SolutionFind the moment of inertia of a uniform rectangular plate of mass M and edges of length 'I' and 'b' about its axis passing through the centre and perpendicular to it.
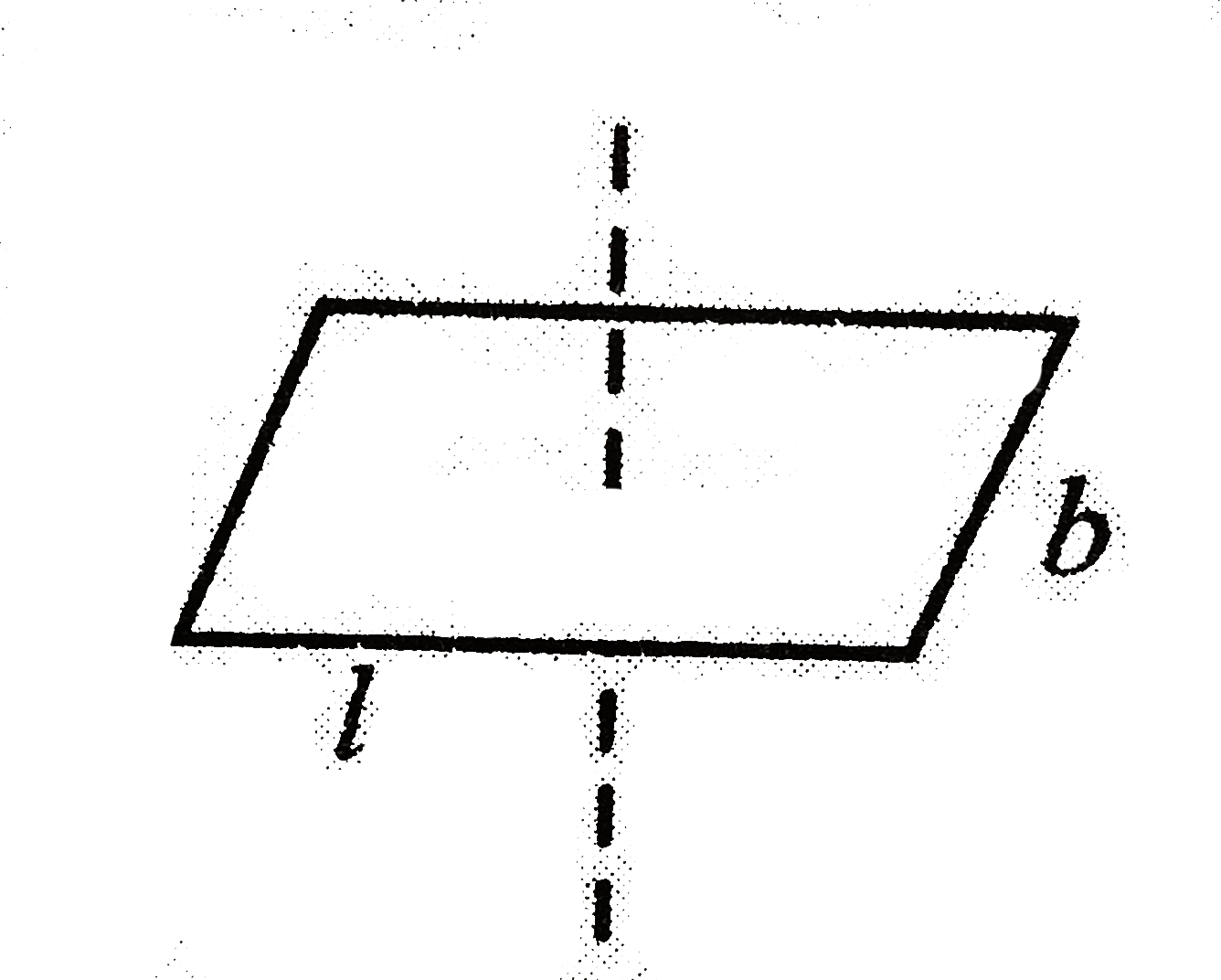
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View Solution
