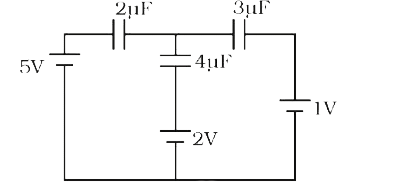
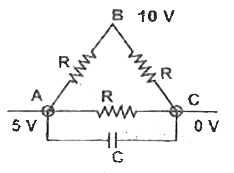
Find the current flowing through the branch AC in the steady state as also the charge on the capacitor C. If the externally applied potentials are now withdrawn, how will the charge on the capacitor vary as a function of time?
(R=1kΩ,C=10μF)
Video Solution
Text Solution
The current through BA=10V−5V1=5mA
Similarly current through AC=5mA,&BC=10mA
steady state charge on C=5V×10μF=50μCIf the potential differences are withdrawn at time t = 0, the charge on the capacitor varies as a function of time as it discharges through the external resistance. The equivalent resistance of the circuit across AC is
2R.R2R+R=23×R=667Ω(≈)
The time constant τ=(2/3R)XXC=6.67msec
The charge across the capacitor decreases exponentiallyq(t)50μCxsxe−t/6.67ms
|
Similar Questions
Knowledge Check
In the circuit given, the charge on capacitor C3 at steady state is
 A6μCB12μCC18μCD24μC
A6μCB12μCC18μCD24μC
The circuit is in a steady state.
The charge in capacitor C1 is
View SolutionThe circuit is in a steady state.
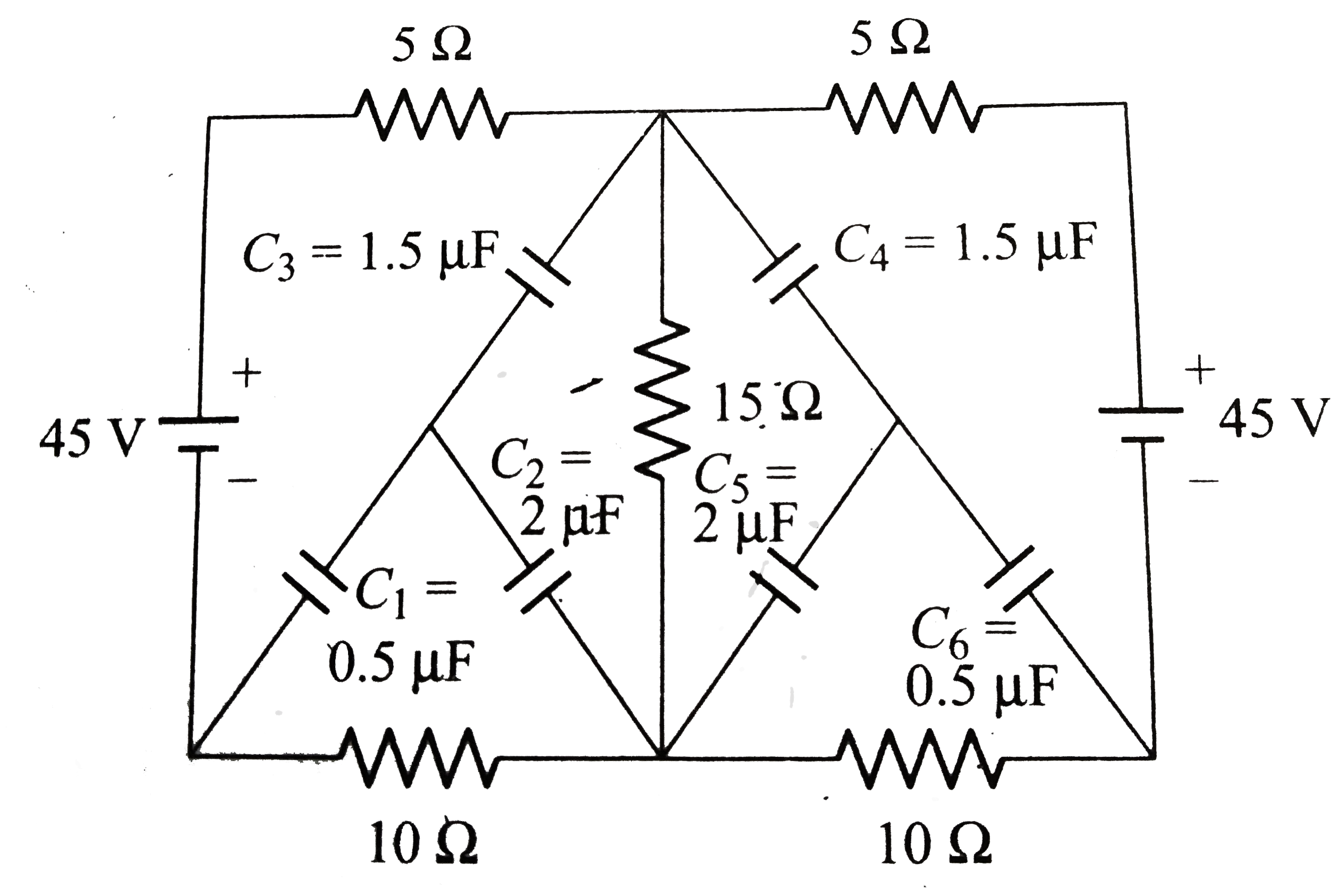
The charge in capacitor C3 is
View SolutionThe circuit is in a steady state.
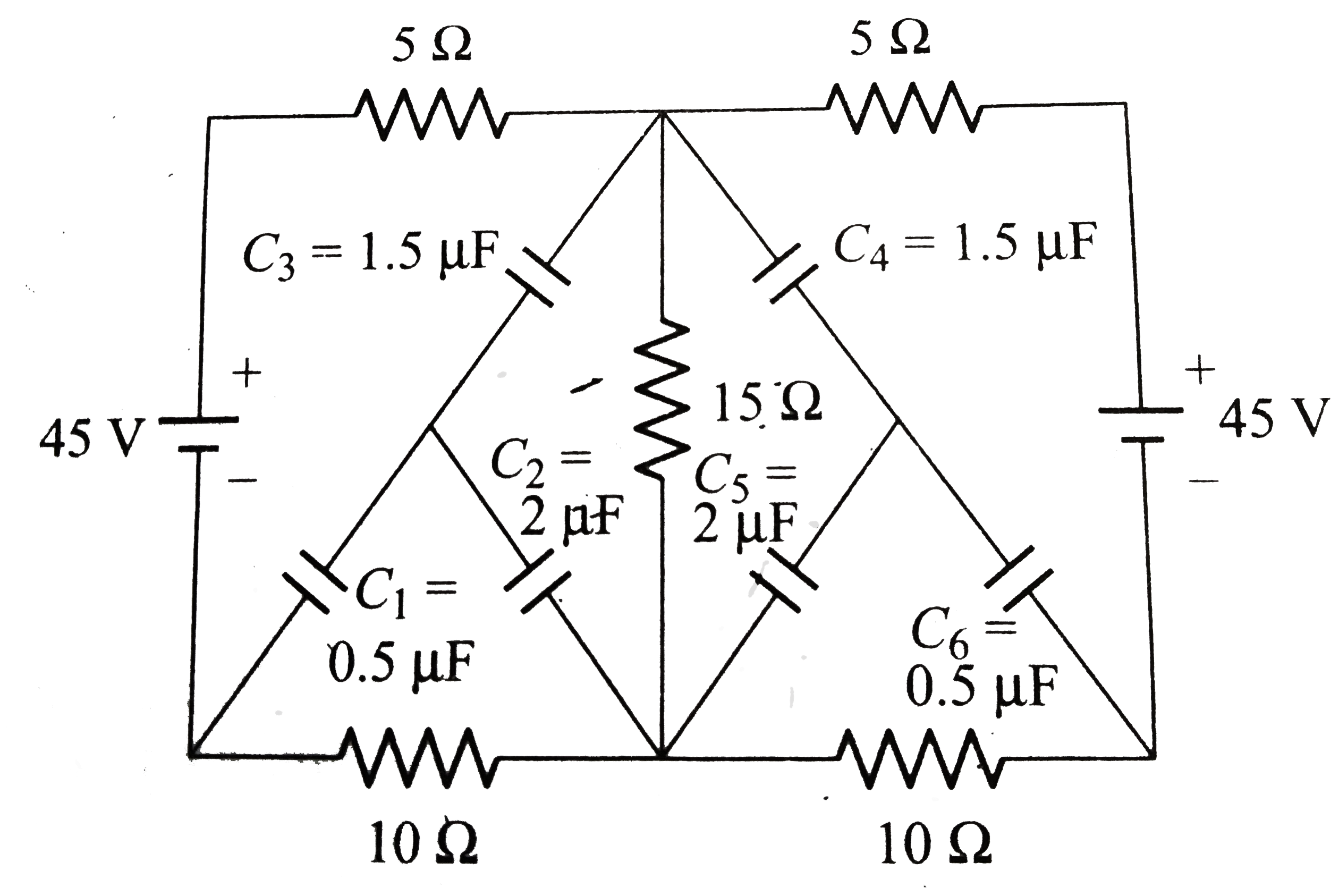
The charge in capacitor C2 is
View SolutionIn steady state, find the charge on the capacitor in (μC) shown in figure.
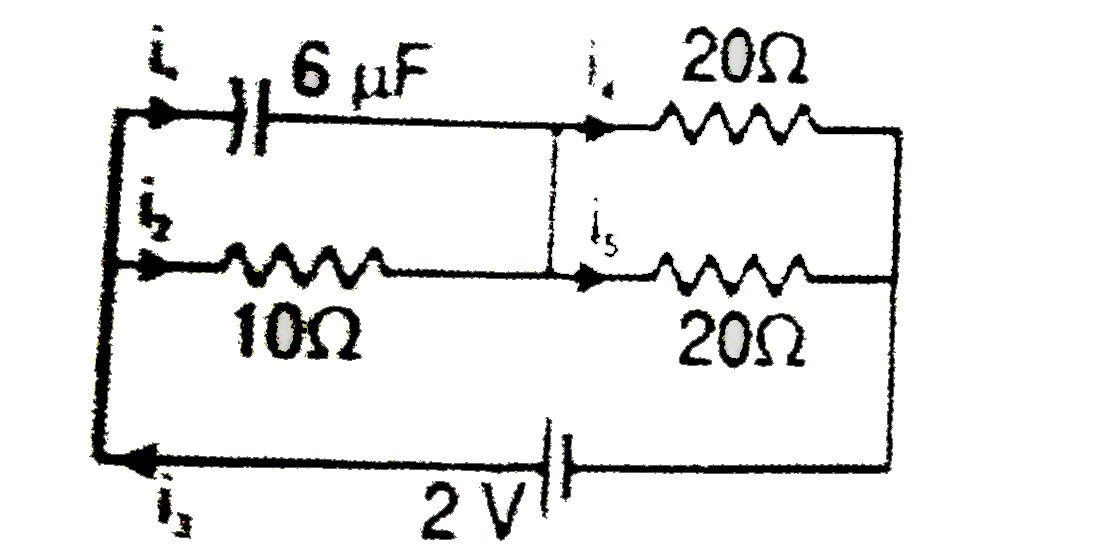
View SolutionThe circuit shown in fig 5.223 is in steady state.
find the charges on the capacitors C1andC2 respectively.

View Solution(a)Find the current I supplied by the battery in the network shown in figure in steady state. (b)find the charge on the capacitor.

View SolutionThe charge on the capacitor is initially zero. Find the charge on the capacitor as a function of time t. All resistors are of equal value R.
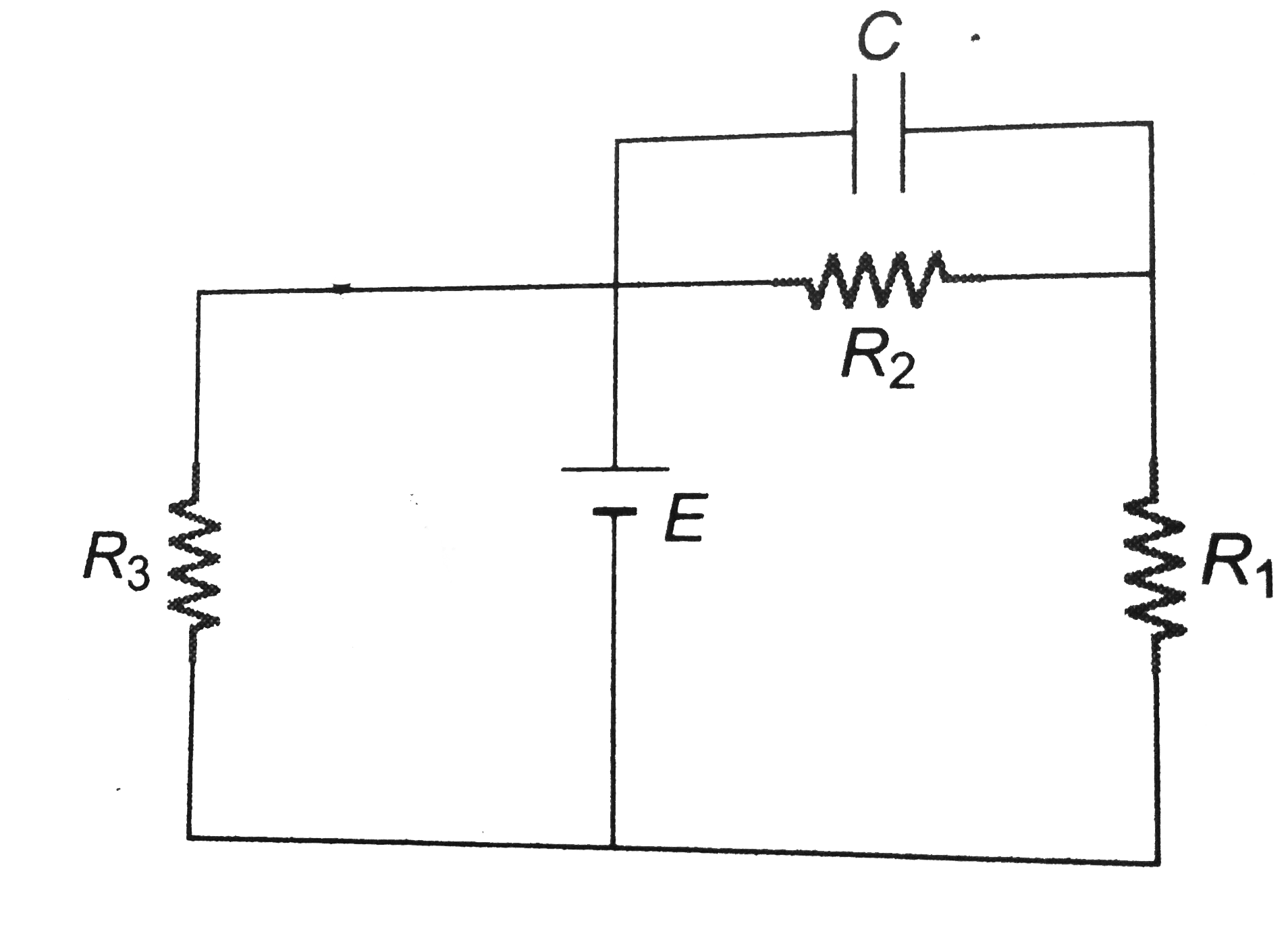
View Solution