A battery of 3.0 V is connected to a resistor dissipating 0.5 W of power . If the terminal voltage of the battery is 2.5 V , the power dissipated within the internal resistance is :
0.072 W
0.125 W
0.50 W
0.10 W
To solve the problem, we need to determine the power dissipated within the internal resistance of the battery. Here’s a step-by-step breakdown of the solution:
Step 1: Identify the given values
- EMF of the battery (E) = 3.0 V
- Terminal voltage (V) = 2.5 V
- Power dissipated across the external resistor (P_R) = 0.5 W
Step 2: Calculate the current flowing through the circuit
Using the formula for power, we can find the current (I) flowing through the external resistor:
PR=I2R⟹I=√PRR
However, we need to first find the resistance (R) using the terminal voltage.
Step 3: Relate terminal voltage, EMF, and internal resistance
The relationship between the EMF, terminal voltage, and current can be expressed as:
V=E−Ir
Where r is the internal resistance of the battery. Rearranging gives:
Ir=E−V⟹Ir=3.0V−2.5V=0.5V
This means:
Ir=0.5V
Step 4: Calculate the current (I)
Since we know the power across the resistor (0.5 W), we can express it in terms of current:
PR=I⋅V⟹0.5W=I⋅2.5V
Solving for I:
I=0.5W2.5V=0.2A
Step 5: Find internal resistance (r)
Now that we have the current, we can find the internal resistance using:
Ir=0.5V⟹r=0.5VI=0.5V0.2A=2.5Ω
Step 6: Calculate the power dissipated in the internal resistance
The power dissipated in the internal resistance can be calculated using the formula:
Pr=I2r
Substituting the values:
Pr=(0.2A)2⋅2.5Ω=0.04A2⋅2.5Ω=0.1W
Conclusion
The power dissipated within the internal resistance of the battery is 0.1 W.
---
- EMF of the battery (E) = 3.0 V
- Terminal voltage (V) = 2.5 V
- Power dissipated across the external resistor (P_R) = 0.5 W
Using the formula for power, we can find the current (I) flowing through the external resistor:
PR=I2R⟹I=√PRR
However, we need to first find the resistance (R) using the terminal voltage.
The relationship between the EMF, terminal voltage, and current can be expressed as:
V=E−Ir
Where r is the internal resistance of the battery. Rearranging gives:
Ir=E−V⟹Ir=3.0V−2.5V=0.5V
This means:
Ir=0.5V
Since we know the power across the resistor (0.5 W), we can express it in terms of current:
PR=I⋅V⟹0.5W=I⋅2.5V
Solving for I:
I=0.5W2.5V=0.2A
Now that we have the current, we can find the internal resistance using:
Ir=0.5V⟹r=0.5VI=0.5V0.2A=2.5Ω
The power dissipated in the internal resistance can be calculated using the formula:
Pr=I2r
Substituting the values:
Pr=(0.2A)2⋅2.5Ω=0.04A2⋅2.5Ω=0.1W
The power dissipated within the internal resistance of the battery is 0.1 W.
Topper's Solved these Questions
Similar Questions
If the power dissipated in 5Ω is 20 W then power dissipated in 4Ω is -

View SolutionA high resistance voltmeter measures the potential difference across a battery to be 9-0 V. On connecting a 24 2 resistor across the terminals of the battery, the voltmeter reads 7.2 V. Calculate the internal resistance of the battery.
View Solution
Knowledge Check
A current of 3A flows through the 2Ω resistor as shown in the circuit. The power dissipated in the 5Ω resistor is
 A5 watt.B4 watt.C2 watt.D1 watt
A5 watt.B4 watt.C2 watt.D1 watt
A battery of emf 10 V is connected with a load resistance of 50 Omega the total power delivered by the battery is 2 W. If load resistance is replaced by R then power delivered is 4 W, the value of R is
View SolutionIn an AC circuit with voltage V and current I, the power dissipated is
View Solutionthe current in a circuit containing a battery connected to 2Ω resistance is 0.9A. When ana additional resistance of 8Ω is connected to the same battery the current observed in the circuit is 0.3A. Then the internal resistance of the battery is xΩ. Find value of x.
View SolutionA resistor of resistance R is connected to an ideal battery. If the value of R is decreased,the power dissipated in the resistor will
View SolutionA resistor of resistance R is connected to an ideal battery. If the value of R is decreased,the power dissipated in the resistor will
View SolutionPower dissipated across the 8Ω resistor in the circuit shown here is 2 w. The power U dissipated in watt units across the 3Ω resistor is .
View SolutionThe figure shows a circuit.
When the circuit is switched on, the ammeter reads 0.5A.
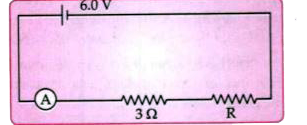
Calculate the power dissipated in the 3Ω resistor.
View Solution
