To measure a potential difference across a resistor of resistance RS, a voltmeter of resistance Ry is used. To measure the potential with a minimum accuracy of 95%, then
Rv=5R
Rv=15R
Rv=10R
Rv,≥19R
The correct Answer is:D
To solve the problem of measuring the potential difference across a resistor RS using a voltmeter of resistance RY with a minimum accuracy of 95%, we can follow these steps:
Step 1: Understand the Circuit
We have a resistor RS and a voltmeter with resistance RY connected in parallel to measure the voltage across RS. According to Ohm's Law, the voltage across the resistor can be expressed as:
V0=I⋅RS
where I is the current flowing through the circuit.
Step 2: Voltage Across the Voltmeter
The voltmeter reading V can be expressed as the voltage across the parallel combination of RS and RY:
V=I⋅RS⋅RYRS+RY
Step 3: Set Up the Accuracy Condition
To achieve a minimum accuracy of 95%, we need the voltmeter reading V to be at least 95% of the actual voltage V0:
V>0.95⋅V0
Substituting the expressions for V and V0:
I⋅RS⋅RYRS+RY>0.95⋅(I⋅RS)
Step 4: Simplify the Inequality
We can cancel I from both sides (assuming I≠0):
RS⋅RYRS+RY>0.95⋅RS
Step 5: Rearranging the Terms
Rearranging gives:
RS⋅RY>0.95⋅RS⋅(RS+RY)
Expanding the right side:
RS⋅RY>0.95⋅R2S+0.95⋅RS⋅RY
Step 6: Isolate RY
Rearranging the terms leads to:
RS⋅RY−0.95⋅RS⋅RY>0.95⋅R2S
Factoring out RY:
RY(1−0.95)>0.95⋅RS
This simplifies to:
0.05⋅RY>0.95⋅RS
Step 7: Solve for RY
Dividing both sides by 0.05 gives:
RY>0.950.05⋅RS
Calculating the right side:
RY>19⋅RS
Conclusion
Thus, to measure the potential difference with a minimum accuracy of 95%, the resistance of the voltmeter RY must be greater than 19⋅RS.
Final Answer
RY≥19⋅RS
---
We have a resistor RS and a voltmeter with resistance RY connected in parallel to measure the voltage across RS. According to Ohm's Law, the voltage across the resistor can be expressed as:
V0=I⋅RS
where I is the current flowing through the circuit.
The voltmeter reading V can be expressed as the voltage across the parallel combination of RS and RY:
V=I⋅RS⋅RYRS+RY
To achieve a minimum accuracy of 95%, we need the voltmeter reading V to be at least 95% of the actual voltage V0:
V>0.95⋅V0
Substituting the expressions for V and V0:
I⋅RS⋅RYRS+RY>0.95⋅(I⋅RS)
We can cancel I from both sides (assuming I≠0):
RS⋅RYRS+RY>0.95⋅RS
Rearranging gives:
RS⋅RY>0.95⋅RS⋅(RS+RY)
Expanding the right side:
RS⋅RY>0.95⋅R2S+0.95⋅RS⋅RY
Rearranging the terms leads to:
RS⋅RY−0.95⋅RS⋅RY>0.95⋅R2S
Factoring out RY:
RY(1−0.95)>0.95⋅RS
This simplifies to:
0.05⋅RY>0.95⋅RS
Dividing both sides by 0.05 gives:
RY>0.950.05⋅RS
Calculating the right side:
RY>19⋅RS
Thus, to measure the potential difference with a minimum accuracy of 95%, the resistance of the voltmeter RY must be greater than 19⋅RS.
RY≥19⋅RS
Similar Questions
Find potential difference across the resistance 300Ω in A and B.
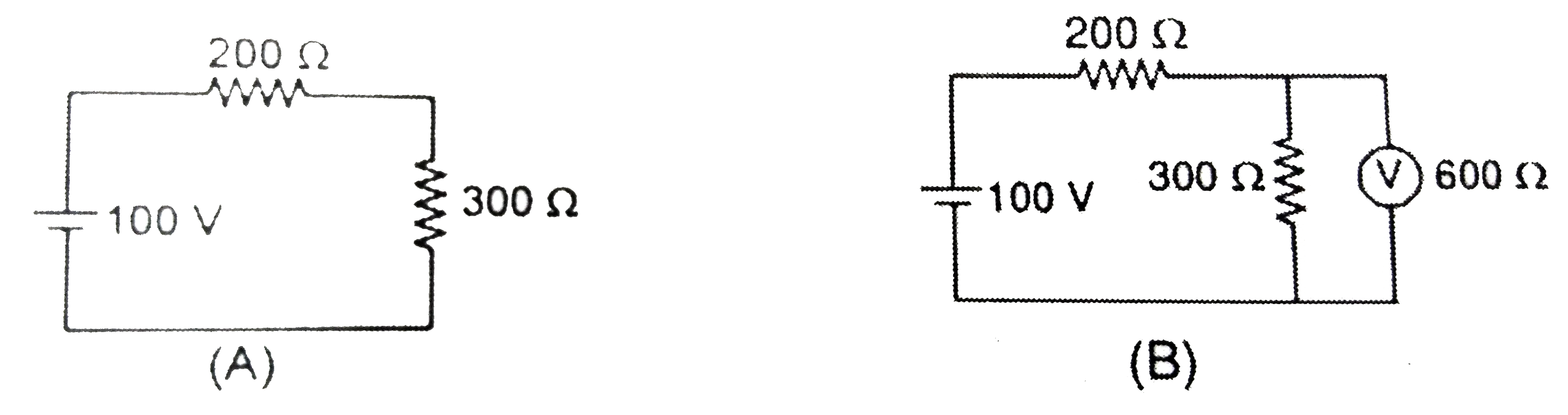
View Solution(a)find the potential drops across the two resistors shown in figure. (b) A voltmeter of resistance (600Ω)is used to measure the potential drop across the (300Ω) resistor.What will be the measured potential drop?
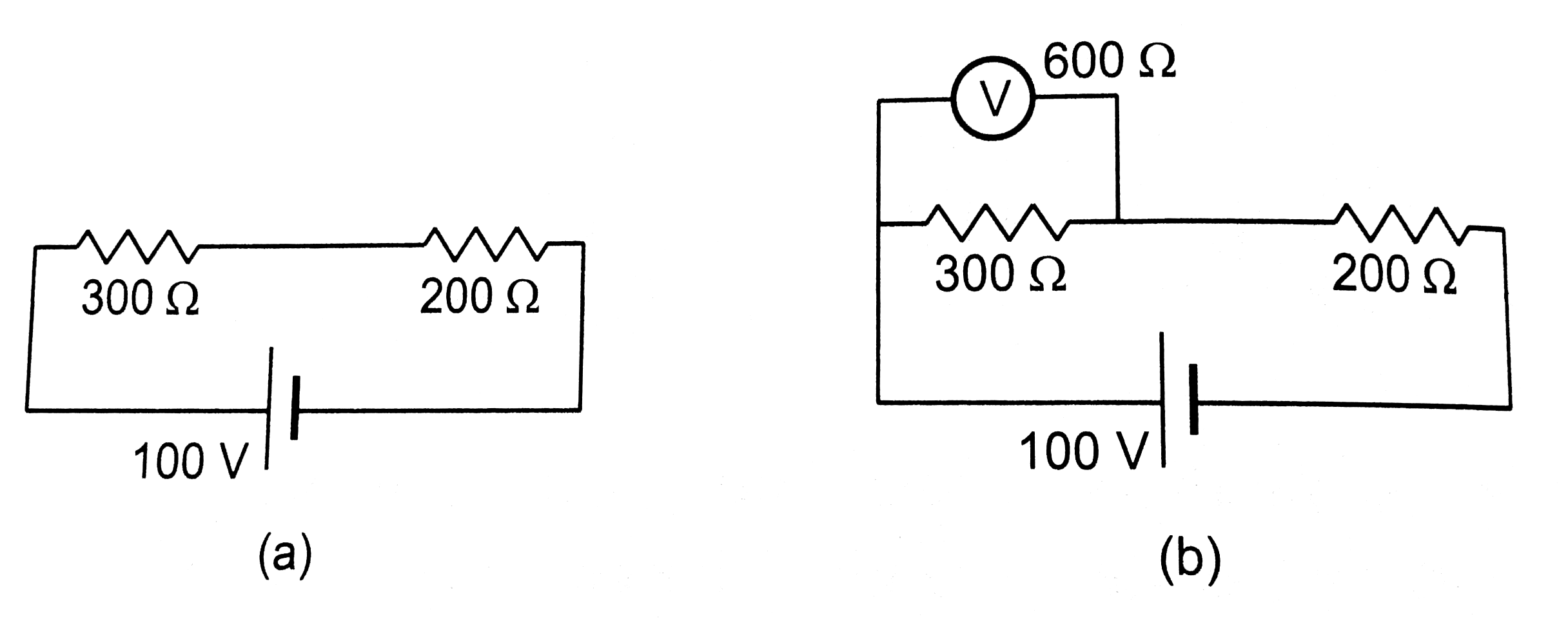
View SolutionPotentiometer measures the potential difference more accurately than a voltmeter, because
View SolutionPotentiometer measures the potential difference more accurately than a voltmeter, because
View SolutionA moving coil voltmeter is generally used to measure the potential difference across a conductor of resistance 'r' carrying a current i. The resistance of voltmeter is R. For more correct measurement of potential difference
View SolutionThe potential difference across 8 ohm resistance is 48 volt as shownin the figure. The value of potential difference across X and Y point will be
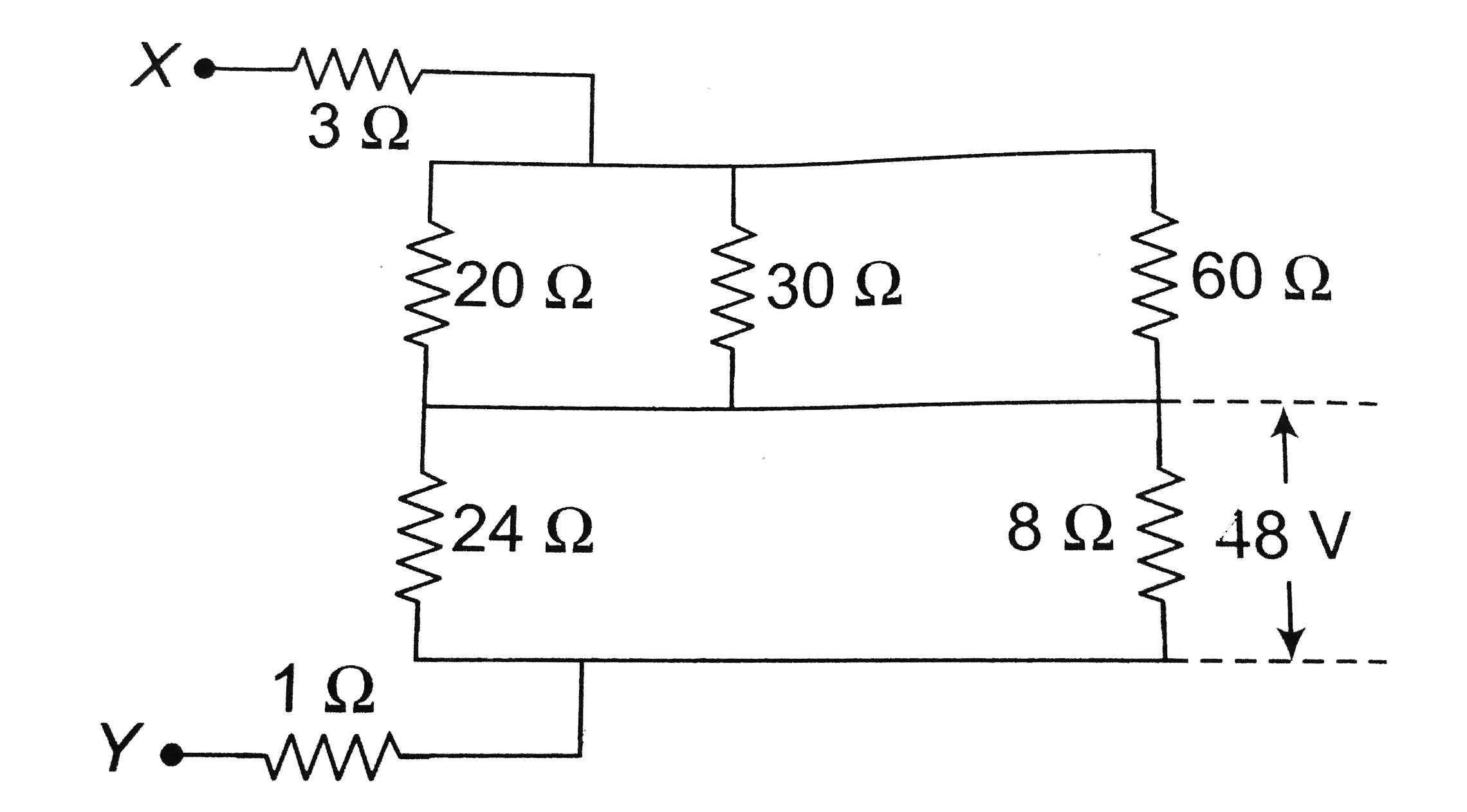
View SolutionThe potential difference across 8 ohm resistance is 48 volt as shownin the figure. The value of potential difference across X and Y point will be

View SolutionTwo resistance of 400Ω and 800Ω are connected in series with 6 volt battery of negligible internal resistance. A voltmeter of resistance 10,000Ω is used to measure the potential difference across 400Ω. The error in measurement of potential difference in volts approximatley is
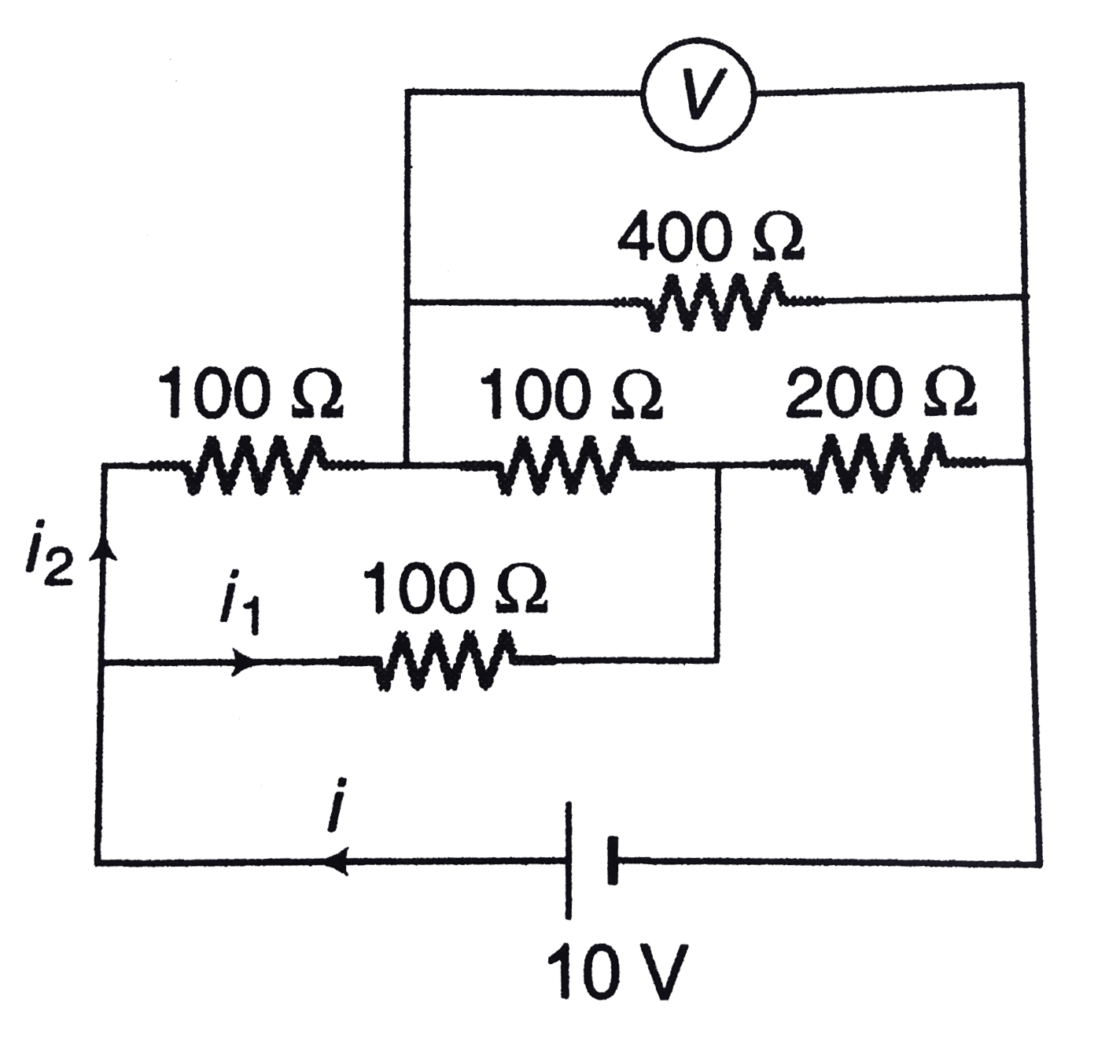
View SolutionAn electrical circuit is shown in figure. Calculate the potential difference across the resistor of 400Ω as will be measured by the voltmeter Vof resistance 400Ω either by applying Kirchhoff's rules or otherwise.
View SolutionThe device used for measuring potential difference is known as:
View Solution
