Two resistance of 400Ω and 800Ω are connected in series with 6 volt battery of negligible internal resistance. A voltmeter of resistance 10,000Ω is used to measure the potential difference across 400Ω. The error in measurement of potential difference in volts approximatley is
0.01
0.02
0.03
0.05
The correct Answer is:D
To solve the problem, we need to calculate the potential difference across the 400 Ω resistor when a voltmeter is connected across it. We will also find the error in the measurement due to the presence of the voltmeter.
1. Identify the Circuit Configuration:
- We have two resistors: R1=400Ω and R2=800Ω connected in series with a 6V battery.
- A voltmeter with a resistance of Rv=10,000Ω is connected across the 400 Ω resistor.
2. Calculate Total Resistance:
- The total resistance of the series circuit without the voltmeter is:
Rtotal=R1+R2=400Ω+800Ω=1200Ω
3. Calculate the Current in the Circuit:
- Using Ohm's law, the current I flowing through the circuit is:
I=VRtotal=6V1200Ω=0.005A(or5mA)
4. Calculate the Voltage Across the 400 Ω Resistor (Without Voltmeter):
- The voltage across the 400 Ω resistor, V1, is given by:
V1=I⋅R1=0.005A⋅400Ω=2V
5. Calculate the Equivalent Resistance with the Voltmeter:
- When the voltmeter is connected, the 400 Ω resistor and the voltmeter are in parallel. The equivalent resistance RAB across the points A and B (where the voltmeter is connected) is:
RAB=R1⋅RvR1+Rv=400Ω⋅10,000Ω400Ω+10,000Ω=4,000,00010,400≈384.62Ω
6. Calculate the New Total Resistance:
- The new total resistance in the circuit is:
Rnew=RAB+R2=384.62Ω+800Ω≈1184.62Ω
7. Calculate the New Current in the Circuit:
- The new current I′ flowing through the circuit is:
I′=VRnew=6V1184.62Ω≈0.00506A
8. Calculate the New Voltage Across the 400 Ω Resistor (With Voltmeter):
- The new voltage V′1 across the 400 Ω resistor is:
V′1=I′⋅R1=0.00506A⋅400Ω≈2.024V
9. Calculate the Error in Measurement:
- The error in measurement ΔV is:
ΔV=V1−V′1=2V−2.024V≈−0.024V
Final Answer:
The error in the measurement of potential difference is approximately −0.024V.
- We have two resistors: R1=400Ω and R2=800Ω connected in series with a 6V battery.
- A voltmeter with a resistance of Rv=10,000Ω is connected across the 400 Ω resistor.
- The total resistance of the series circuit without the voltmeter is:
Rtotal=R1+R2=400Ω+800Ω=1200Ω
- Using Ohm's law, the current I flowing through the circuit is:
I=VRtotal=6V1200Ω=0.005A(or5mA)
- The voltage across the 400 Ω resistor, V1, is given by:
V1=I⋅R1=0.005A⋅400Ω=2V
- When the voltmeter is connected, the 400 Ω resistor and the voltmeter are in parallel. The equivalent resistance RAB across the points A and B (where the voltmeter is connected) is:
RAB=R1⋅RvR1+Rv=400Ω⋅10,000Ω400Ω+10,000Ω=4,000,00010,400≈384.62Ω
- The new total resistance in the circuit is:
Rnew=RAB+R2=384.62Ω+800Ω≈1184.62Ω
- The new current I′ flowing through the circuit is:
I′=VRnew=6V1184.62Ω≈0.00506A
- The new voltage V′1 across the 400 Ω resistor is:
V′1=I′⋅R1=0.00506A⋅400Ω≈2.024V
- The error in measurement ΔV is:
ΔV=V1−V′1=2V−2.024V≈−0.024V
The error in the measurement of potential difference is approximately −0.024V.
Similar Questions
Two resistances of 100 ohm and 200 ohm are connected in series with a battery of emf 4 volt and negligible internal resistance. A voltmeter of resistance 200 ohm is used to measure voltage across the two resistances separately. Calculate the voltage indicated.
View SolutionA voltmeter with resistance 500Ω is used to measure the emf of a cell of internal resistance 4Ω. The percentage error in the reading of the voltmeter will be
View SolutionFigure below shows two resistors R1andR2 connected to a battery having an emf of 40 V and negligible internal resistance. A voltmeter having a resistance of 300 Ω is used to measure potential difference across R1 Find the reading of the voltmeter.
 View Solution
View SolutionResistance of 100Ω and 200Ω are connected in series with 220 V mains. When a voltmeter of 1000Ω resistance is connected in parallel to100Ω , then the reading of voltmeter is
View Solution(a)find the potential drops across the two resistors shown in figure. (b) A voltmeter of resistance (600Ω)is used to measure the potential drop across the (300Ω) resistor.What will be the measured potential drop?
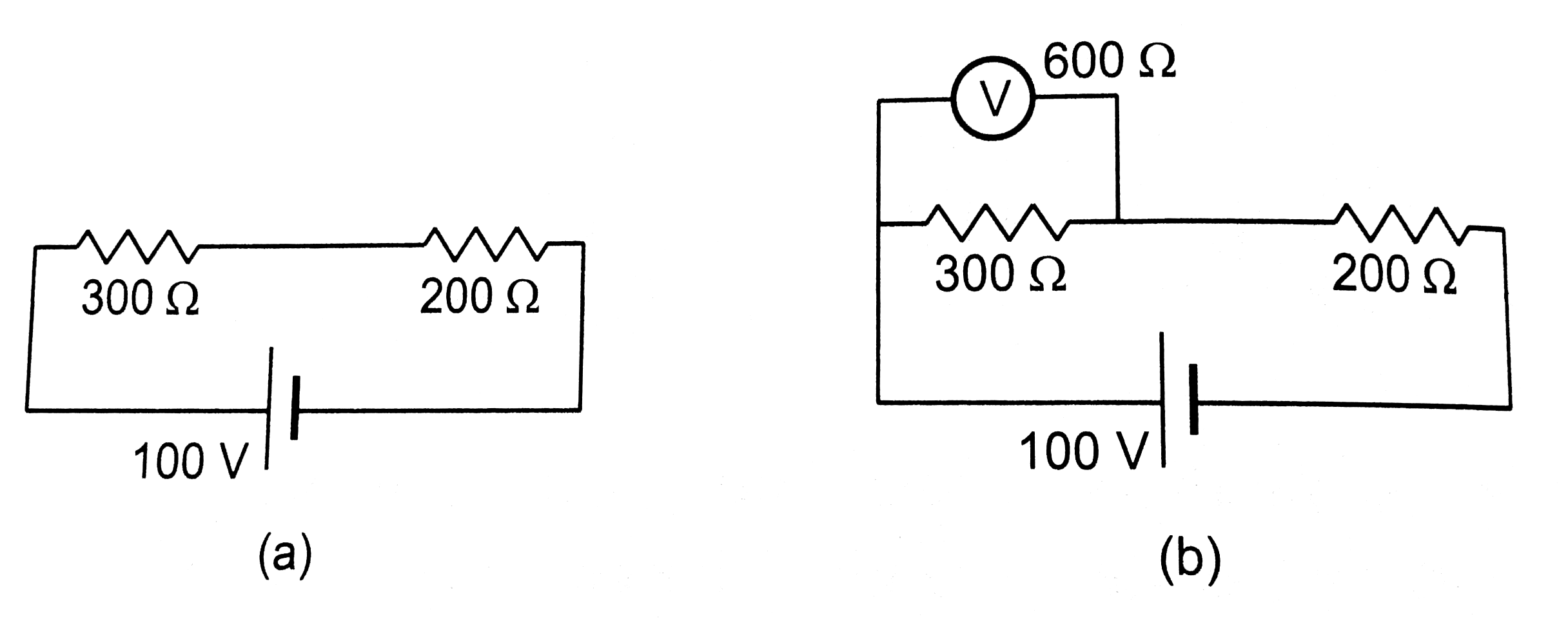 View Solution
View SolutionTwo resistor 400Ω and 800Ω connected in series across a 6 V battery . Reading of Voltmeter of 10kΩ across 400Ω resistor is close to :
View SolutionConsider the diagram shown below.
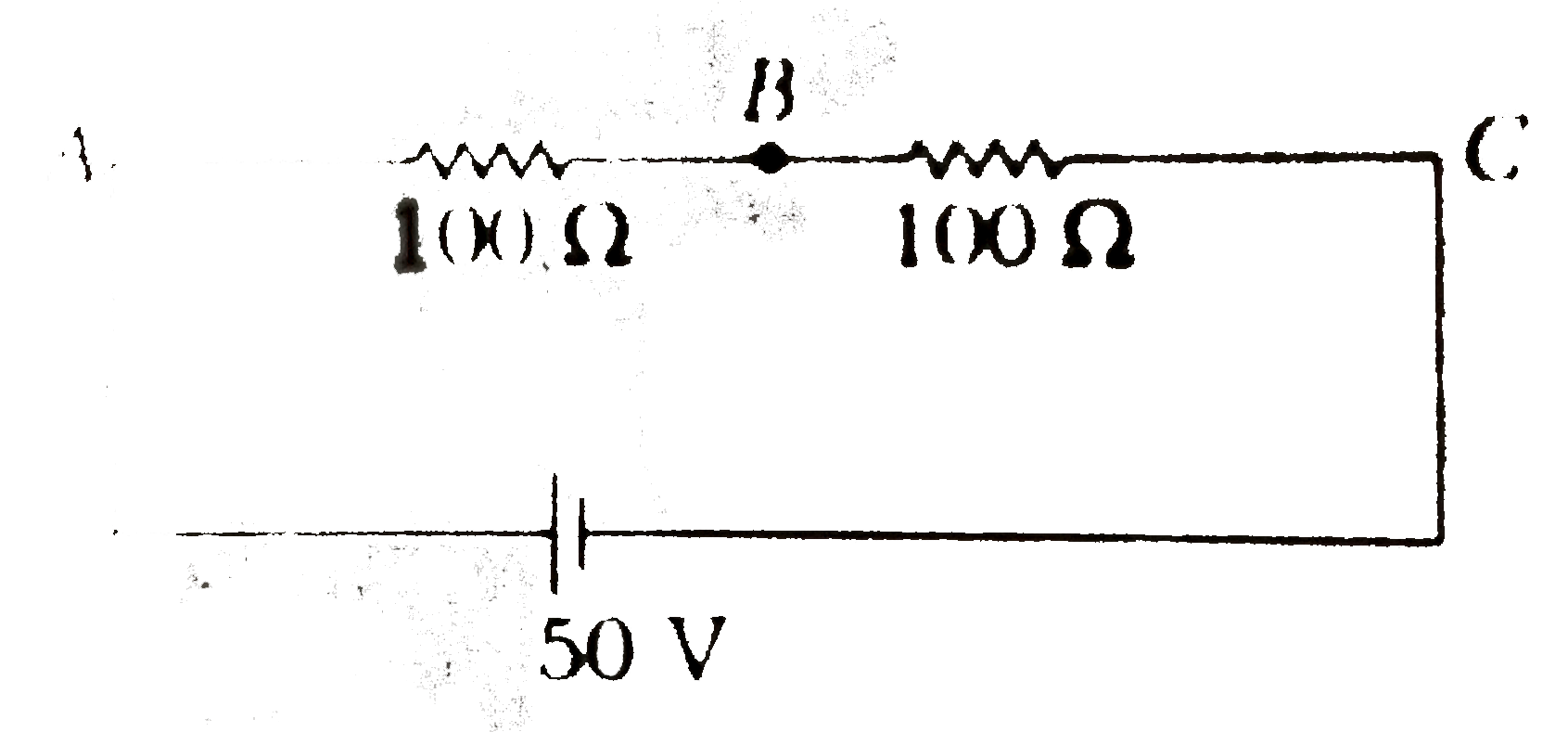
A Voltmeter of resistance 150Ω is connected across A and B. The potential drop across B and C measured by voltmeter isView SolutionThe internal resistances of two cells shown are 0.1Ω and 0.3Ω. If R=0.2Ω, its potential difference across the cell
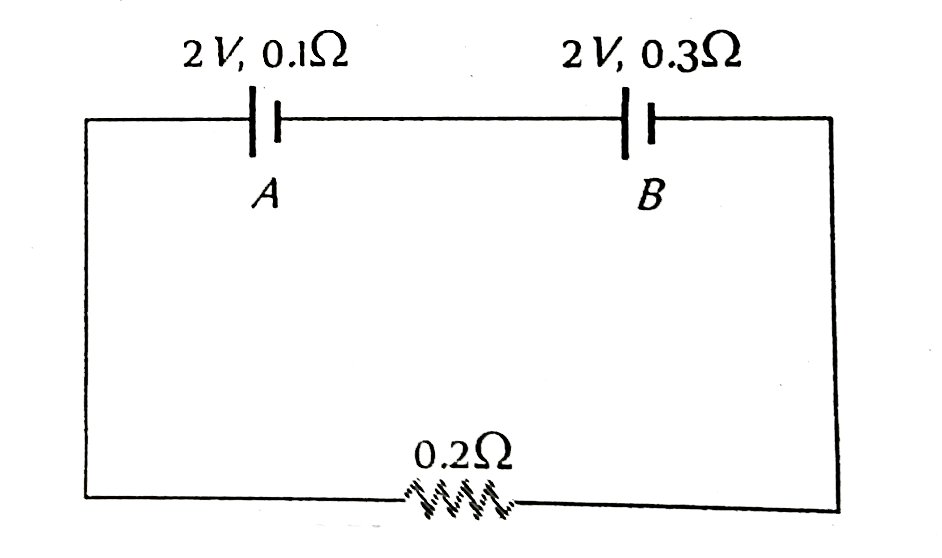 View Solution
View SolutionFind potential difference across the resistance 300Ω in A and B.
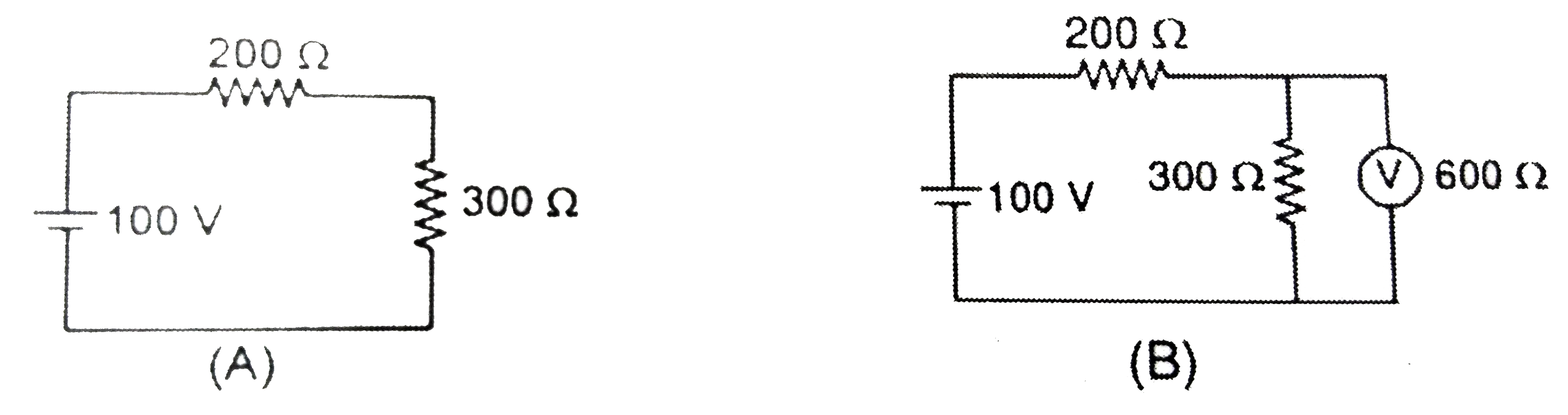 View Solution
View SolutionTwo resistances R_1, and R_2, each of 100 Omega 22 Omega are connected with potential source of 40 V between A and B. If resistance of voltmeter is 200 Omega, then reading of voltmeter is
 View Solution
View Solution

