The maximum power dissipated by external resistance R by a cell of an external omf E and internal resistance r is E2/4R which is obtained for
R<r
R<r
R=r
any value of R.
The correct Answer is:C
To solve the problem, we need to understand the concept of maximum power transfer theorem in electrical circuits. The theorem states that maximum power is transferred to the load (external resistance R) when the load resistance is equal to the source's internal resistance (r).
1. Understanding the Power Dissipation Formula:
The power (P) dissipated across an external resistance (R) connected to a cell with an EMF (E) and internal resistance (r) can be expressed as:
P=E2(R+r)2⋅R
2. Finding Maximum Power Condition:
To find the condition for maximum power, we need to differentiate the power equation with respect to R and set the derivative to zero. However, we can use the maximum power transfer theorem directly, which states that maximum power is transferred when:
R=r
3. Substituting the Condition into the Power Formula:
If we substitute R=r into the power formula, we can find the maximum power:
Pmax=E2(R+r)2⋅R
Substituting R=r:
Pmax=E2(r+r)2⋅r=E2(2r)2⋅r=E24r
4. Conclusion:
Therefore, the maximum power dissipated by the external resistance R is given by:
Pmax=E24R
This shows that the maximum power is achieved when the external resistance R is equal to the internal resistance r.
Final Answer:
The maximum power dissipated by external resistance R by a cell of external EMF E and internal resistance r is E24R, which is obtained when R=r.
The power (P) dissipated across an external resistance (R) connected to a cell with an EMF (E) and internal resistance (r) can be expressed as:
P=E2(R+r)2⋅R
To find the condition for maximum power, we need to differentiate the power equation with respect to R and set the derivative to zero. However, we can use the maximum power transfer theorem directly, which states that maximum power is transferred when:
R=r
If we substitute R=r into the power formula, we can find the maximum power:
Pmax=E2(R+r)2⋅R
Substituting R=r:
Pmax=E2(r+r)2⋅r=E2(2r)2⋅r=E24r
Therefore, the maximum power dissipated by the external resistance R is given by:
Pmax=E24R
This shows that the maximum power is achieved when the external resistance R is equal to the internal resistance r.
The maximum power dissipated by external resistance R by a cell of external EMF E and internal resistance r is E24R, which is obtained when R=r.
Similar Questions
The maximum power dissipated in an external resistance R, when connected to a cell of emf E and internal resistance r, will be
View SolutionFor maximum power from battery the internal resistance of battery r is
View Solution
A uniform potentiometer wire AB of length 100 cm has a resistance of 5Ω and it is connected in series with an external resistance R and a cell of emf 6 V and negligible internal resistance. If a source of potential drop 2 V is balanced against a length of 60 cm of the potentiometer wire, the value of resistance R is
View SolutionA cell of emf E having an internal resistance R varies with R as shown in figure by the curve

View SolutionA potentiometer arrangement is shows in Fig. 6.62. The driver cell has emf e and internal resistance r. The resistance of potentiometer wire AB is R.F is the cell of emf e/3 and internal resistance r/3. Balance point (J) can be obtained for all finite value of
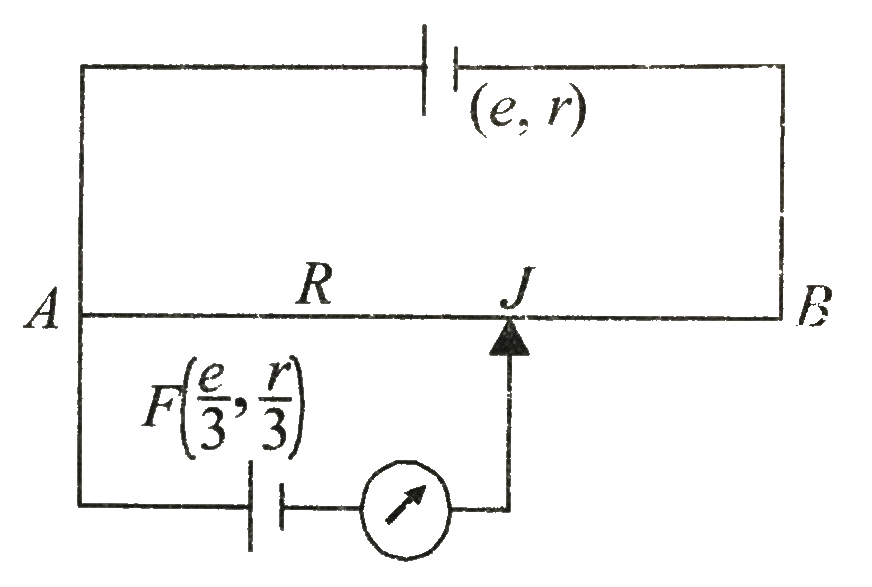
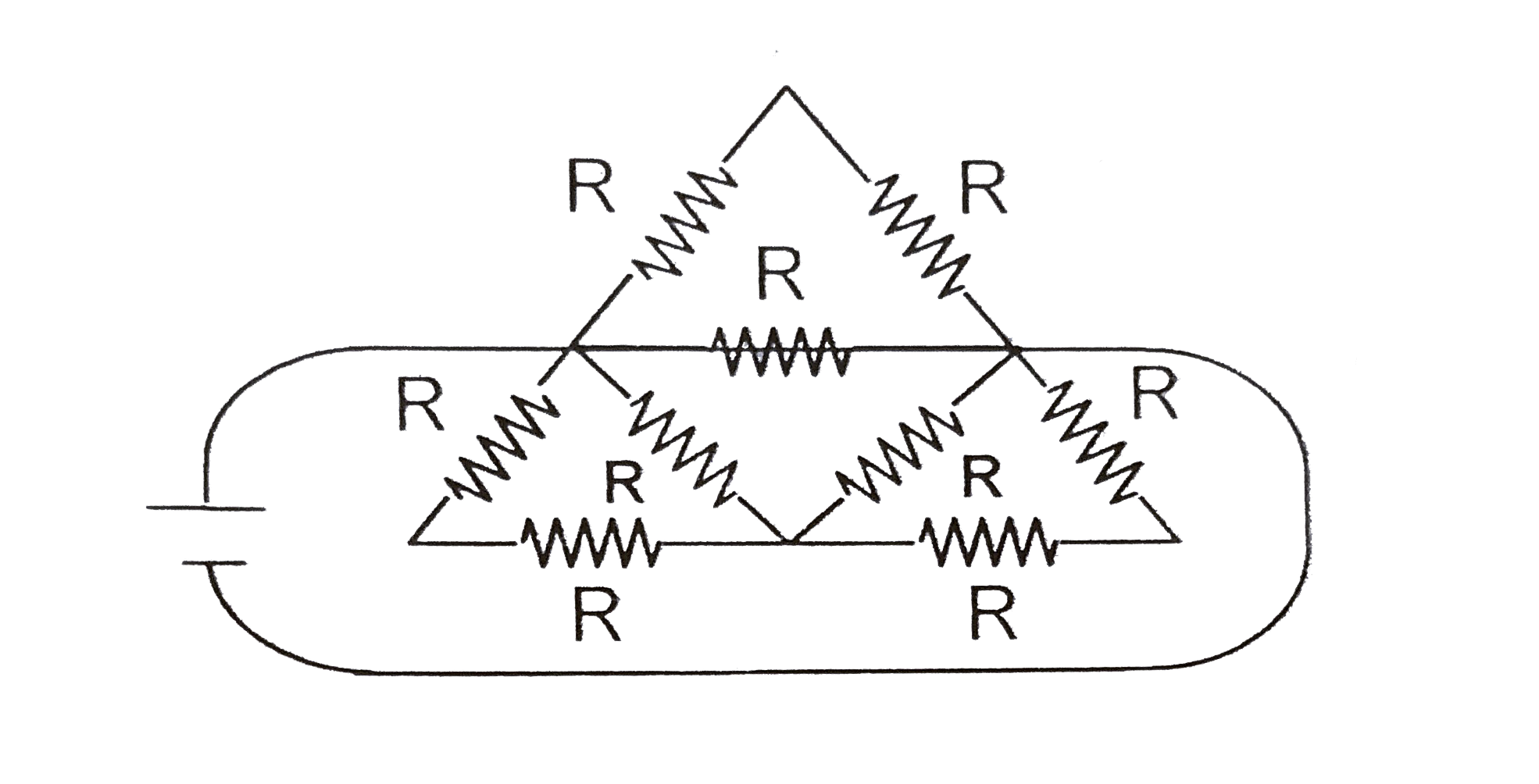
View SolutionThe power dissipated in the resistance R, in the circuit as shown in the figure, is maximum if R is equal to
View Solutionn. cells, each of emf .e. and internal resistance .r. are joined in series to form a row. .m. such rows are connected in parallel to form a battery of N = mn cells. This battery is connected to an external resistance .R..
(i) What is the emf of this battery and how much is its internal resistance ?
Show that current .l. flowing through the external resistance .R. is given by-
I=NemR+nr
View Solution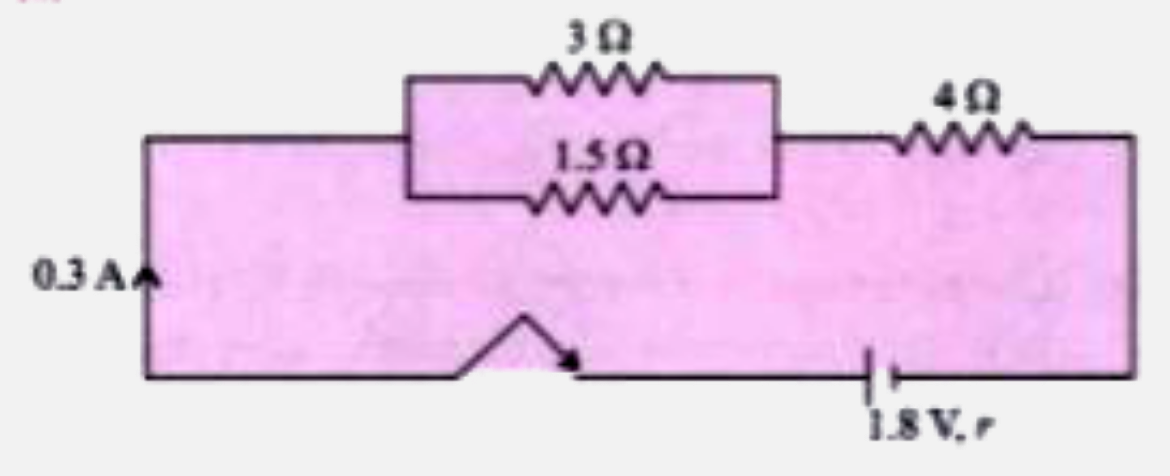
The diagram above shows three resistors connected across a cell of e.m.f. 1.8 V and internal resistance r. Calculate :
The internal resistance r.
View SolutionIn the figure the potentiometer wire AB of length L and resistance 9 r is joined to the cell D of e.m.f ε and internal resistance r. The emf of cell C is ε2 and its internal resistance is 2r.The galvanometer G will show on deflection when the length AJ is
View SolutionA battery is of emt E and internal resistance R. The value of external resistance r so that the power across eternal resistance is maximum :
View Solution

