The maximum power dissipated in an external resistance R, when connected to a cell of emf E and internal resistance r, will be
E2r
E22r
E23r
E24r
The correct Answer is:D
To find the maximum power dissipated in an external resistance R when connected to a cell of emf E and internal resistance r, we can follow these steps:
1. Understand the Circuit Configuration:
We have a circuit consisting of a battery with an emf E and an internal resistance r. An external resistance R is connected in series with the battery.
2. Condition for Maximum Power Dissipation:
According to the maximum power transfer theorem, the power dissipated in the external resistance R is maximized when R is equal to the internal resistance r. Therefore, we set:
R=r
3. Calculate the Current in the Circuit:
The total resistance in the circuit is the sum of the internal resistance and the external resistance:
Rtotal=R+r=r+r=2r
The current I flowing through the circuit can be calculated using Ohm's law:
I=ERtotal=E2r
4. Power Dissipated in the External Resistance:
The power P dissipated in the external resistance R can be expressed as:
P=I2R
Substituting the expression for I:
P=(E2r)2R
5. Substituting R with r:
Since we have established that for maximum power, R=r, we can substitute R in the power equation:
P=(E2r)2r
6. Simplifying the Expression:
Now, simplifying the expression:
P=E24r2⋅r=E24r
7. Final Result:
Therefore, the maximum power dissipated in the external resistance R is:
Pmax=E24r
We have a circuit consisting of a battery with an emf E and an internal resistance r. An external resistance R is connected in series with the battery.
According to the maximum power transfer theorem, the power dissipated in the external resistance R is maximized when R is equal to the internal resistance r. Therefore, we set:
R=r
The total resistance in the circuit is the sum of the internal resistance and the external resistance:
Rtotal=R+r=r+r=2r
The current I flowing through the circuit can be calculated using Ohm's law:
I=ERtotal=E2r
The power P dissipated in the external resistance R can be expressed as:
P=I2R
Substituting the expression for I:
P=(E2r)2R
Since we have established that for maximum power, R=r, we can substitute R in the power equation:
P=(E2r)2r
Now, simplifying the expression:
P=E24r2⋅r=E24r
Therefore, the maximum power dissipated in the external resistance R is:
Pmax=E24r
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason
18 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
The maximum power dissipated by external resistance R by a cell of an external omf E and internal resistance r is E2/4R which is obtained for
View Solution
A uniform potentiometer wire AB of length 100 cm has a resistance of 5Ω and it is connected in series with an external resistance R and a cell of emf 6 V and negligible internal resistance. If a source of potential drop 2 V is balanced against a length of 60 cm of the potentiometer wire, the value of resistance R is
View Solution
Knowledge Check
If n cells each of emf E and internal resistance rare connected in parallel, then the total emf and internal resistances will be
Aε,rnBε,nrCnε,rnDnε,nrIn the series combination of n cells each cell having emf ε and internal resistance r. If three cells are wrongly connected, then total emf and internal resistance of this combination will be
Anε,(nr−3r)B(nε−2r),nrC(nε−4ε),nrD(nε−6ε),nr
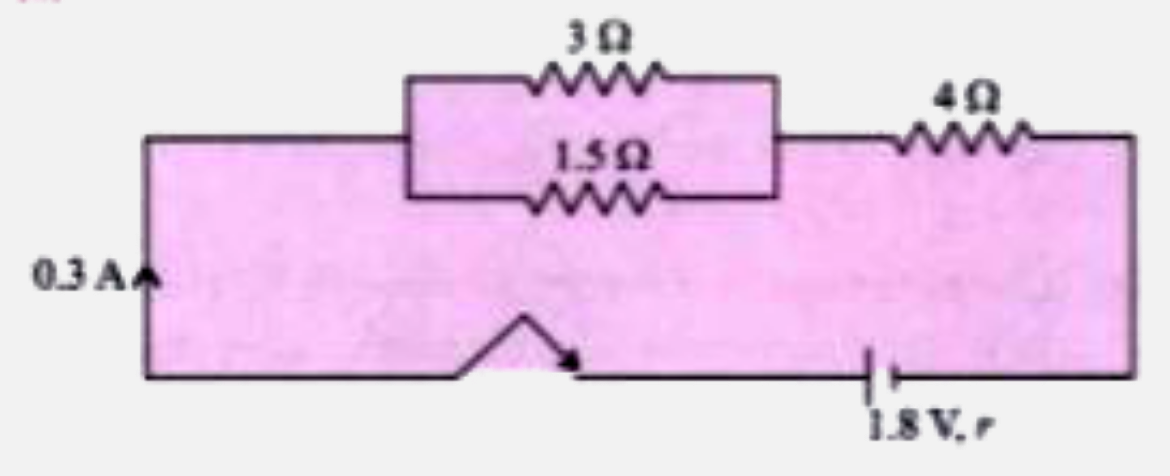
The diagram above shows three resistors connected across a cell of e.m.f. 1.8 V and internal resistance r. Calculate :
The internal resistance r.
View SolutionStatement I: When an external resistor of resistance R (connected across a cell to internal resistance r ) is varied, power consumed by resistance R is maximum when R = r.
Statement II: Power consumed by a resistor of constant resistance R is maximum when current through it is maximum.
View SolutionA battery of emf (epsilon) and internal resistance r is connected across a load resistanvce (RundersetL). The plot between output power and load resistance is shown in the figure.
_PHY_E05_024_Q01.png) value of emf (ε) and internal resistance respectively will be
value of emf (ε) and internal resistance respectively will be
View SolutionA cell of internal resistance r drivers current through an external resistance R. The power delivered by the to the external resistance will be maximum when:
View SolutionWhen a celll is connected to an external resistance R1, current through it is i1. When the same cell is connected to an external resistance R2, current through it is i2. Calculate the emf and internal resisance of the cell.
View SolutionThousand cells of same emf E and same internal resistance r are connected is series in same order without an external resistance . The potential drop across 399 cells is found to be .
View Solution
