A charge Q is given to the plates of an isolated capacitor of capacitance C. Now, the terminals of this capacitor are connected to the terminals of an inductor L at t = 0. After how much time will the energy stored in the capacitor and the Inductor become equal?
π√(LC)/2
π√(LC)/4
5π√(LC)/2
π√(LC)
The correct Answer is:B
To solve the problem, we need to find the time t when the energy stored in the capacitor equals the energy stored in the inductor after connecting them at t=0.
1. Energy in the Capacitor:
The energy UC stored in a capacitor with charge Q and capacitance C is given by the formula:
UC=Q22C
2. Energy in the Inductor:
The energy UL stored in an inductor with current I and inductance L is given by:
UL=12LI2
3. Condition for Equal Energy:
We want to find the time t when the energies in the capacitor and inductor are equal:
UC=UL
Therefore,
Q22C=12LI2
4. Relating Current and Charge:
The current I in the circuit can be expressed as the rate of change of charge Q on the capacitor:
I=−dQdt
Substituting this into the energy equation gives:
Q22C=12L(−dQdt)2
5. Differential Equation:
Rearranging the equation leads to:
Q2C=L(dQdt)2
Taking the square root of both sides, we have:
dQdt=±Q√LC
6. Separation of Variables:
We can separate variables to solve for Q:
dQQ=±dt√LC
7. Integrating:
Integrating both sides gives:
ln|Q|=±t√LC+C1
Exponentiating both sides leads to:
Q=Q0e±t√LC
where Q0 is the initial charge.
8. Finding Time When Energies are Equal:
We know that the energy in the capacitor will be half of the initial energy when:
Q=Q0√2
Setting Q=Q0√2 in our equation:
Q0√2=Q0e−t√LC
Dividing both sides by Q0 (assuming Q0≠0):
1√2=e−t√LC
9. Taking Logarithm:
Taking the natural logarithm of both sides:
−t√LC=ln(1√2)
Simplifying gives:
t=−√LCln(1√2)=√LC⋅12ln(2)
10. Final Result:
Thus, the time t when the energy stored in the capacitor and the inductor becomes equal is:
t=√LC2ln(2)
The energy UC stored in a capacitor with charge Q and capacitance C is given by the formula:
UC=Q22C
The energy UL stored in an inductor with current I and inductance L is given by:
UL=12LI2
We want to find the time t when the energies in the capacitor and inductor are equal:
UC=UL
Therefore,
Q22C=12LI2
The current I in the circuit can be expressed as the rate of change of charge Q on the capacitor:
I=−dQdt
Substituting this into the energy equation gives:
Q22C=12L(−dQdt)2
Rearranging the equation leads to:
Q2C=L(dQdt)2
Taking the square root of both sides, we have:
dQdt=±Q√LC
We can separate variables to solve for Q:
dQQ=±dt√LC
Integrating both sides gives:
ln|Q|=±t√LC+C1
Exponentiating both sides leads to:
Q=Q0e±t√LC
where Q0 is the initial charge.
We know that the energy in the capacitor will be half of the initial energy when:
Q=Q0√2
Setting Q=Q0√2 in our equation:
Q0√2=Q0e−t√LC
Dividing both sides by Q0 (assuming Q0≠0):
1√2=e−t√LC
Taking the natural logarithm of both sides:
−t√LC=ln(1√2)
Simplifying gives:
t=−√LCln(1√2)=√LC⋅12ln(2)
Thus, the time t when the energy stored in the capacitor and the inductor becomes equal is:
t=√LC2ln(2)
Similar Questions
Knowledge Check
A fully charged capacitor C with initial charge q0 is connected to a coil of self inductance L at t=0. The time at which the energy is stored equally between the electric and the magnetic fields is
Aπ4√LCB2π√LCC√LCDπ√LC
A 12 pF capacitor is connected to a 50 V battery. How much electrostatic energy is stored in the capacitor ?
View SolutionA series RLC circuit is connected to an ac generator. The instant at which current in the circuit is zero, the energy stored in the capacitor and inductor are:
View SolutionA capacitor of capacitance Chas initial charge Q0 and connected to an inductor L as shown. Att=0 switch S is closed. The current through the inductor when energy in the capacitor is three times the energy of inductor is

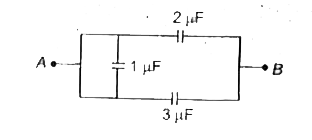
View SolutionIn the given circuit the charge on the plates of 1 μF capacitor, when 100 V battery is connected to the terminals A and B will be
View SolutionA cylindrical capacitor has charge Q and length L. If both the charge and length of the capacitor are doubled by keeping other parameters fixed, the energy stored in the capacitor
View SolutionShow that in the free oscillations of an LC circuit, the sum of energies stored in the capacitor and and the inductor is constant in time.
View SolutionAn uncharged capacitor is connected in series with a resistor and a battery. The charging of the capacitor starts at t=0. The rate at which energy stored in the capacitor:-
View Solution