A cylindrical capacitor has charge Q and length L. If both the charge and length of the capacitor are doubled by keeping other parameters fixed, the energy stored in the capacitor
remains same
increases two times
decreases two times
increases four times
The correct Answer is:B
To solve the problem, we need to analyze how the energy stored in a cylindrical capacitor changes when both the charge and the length of the capacitor are doubled.
1. Understanding the Energy Stored in a Capacitor:
The energy (E) stored in a capacitor is given by the formula:
E=12Q2C
where Q is the charge and C is the capacitance.
2. Capacitance of a Cylindrical Capacitor:
The capacitance C of a cylindrical capacitor is given by:
C=2πϵ0Lln(B/A)
where L is the length of the capacitor, B is the outer radius, A is the inner radius, and ϵ0 is the permittivity of free space.
3. Initial Energy Expression:
Substituting the expression for capacitance into the energy formula, we have:
E=12Q2ln(B/A)2πϵ0L
4. Doubling Charge and Length:
If both the charge Q and the length L are doubled, we denote the new charge as Q′=2Q and the new length as L′=2L.
5. New Capacitance:
The new capacitance C′ after doubling the length becomes:
C′=2πϵ0(2L)ln(B/A)=2⋅2πϵ0Lln(B/A)=2C
6. New Energy Expression:
Now substituting Q′ and C′ into the energy formula:
E′=12(2Q)2C′=124Q22C=2Q2C
7. Relating New Energy to Initial Energy:
From the initial energy expression E=12Q2C, we can see that:
E′=2⋅12Q2C=2E
8. Conclusion:
The energy stored in the capacitor after doubling both the charge and the length is:
E′=2E
Therefore, the energy stored in the capacitor increases by a factor of 2.
Final Answer:
The energy stored in the capacitor increases two times.
The energy (E) stored in a capacitor is given by the formula:
E=12Q2C
where Q is the charge and C is the capacitance.
The capacitance C of a cylindrical capacitor is given by:
C=2πϵ0Lln(B/A)
where L is the length of the capacitor, B is the outer radius, A is the inner radius, and ϵ0 is the permittivity of free space.
Substituting the expression for capacitance into the energy formula, we have:
E=12Q2ln(B/A)2πϵ0L
If both the charge Q and the length L are doubled, we denote the new charge as Q′=2Q and the new length as L′=2L.
The new capacitance C′ after doubling the length becomes:
C′=2πϵ0(2L)ln(B/A)=2⋅2πϵ0Lln(B/A)=2C
Now substituting Q′ and C′ into the energy formula:
E′=12(2Q)2C′=124Q22C=2Q2C
From the initial energy expression E=12Q2C, we can see that:
E′=2⋅12Q2C=2E
The energy stored in the capacitor after doubling both the charge and the length is:
E′=2E
Therefore, the energy stored in the capacitor increases by a factor of 2.
The energy stored in the capacitor increases two times.
Similar Questions
Find the charge stored in the capacitor.
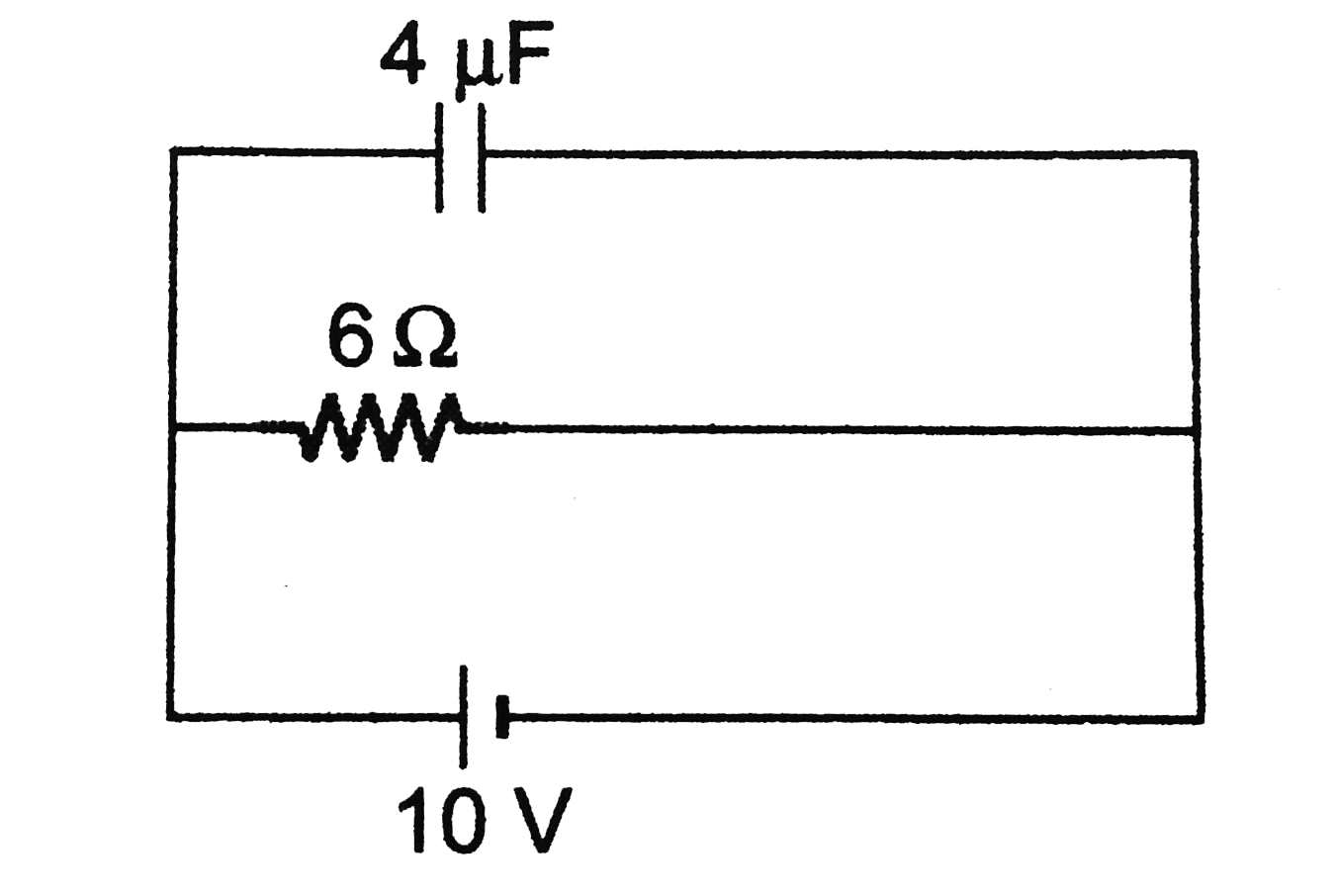
View SolutionFind the charge stored in the capacitor.
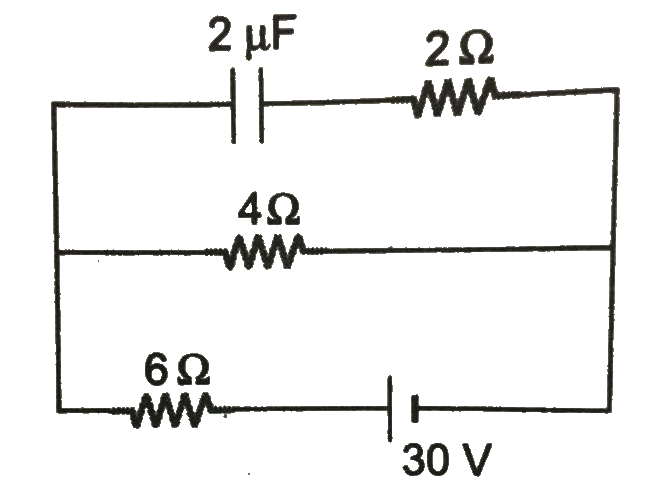
View SolutionFind the charge stored in the capacitor.
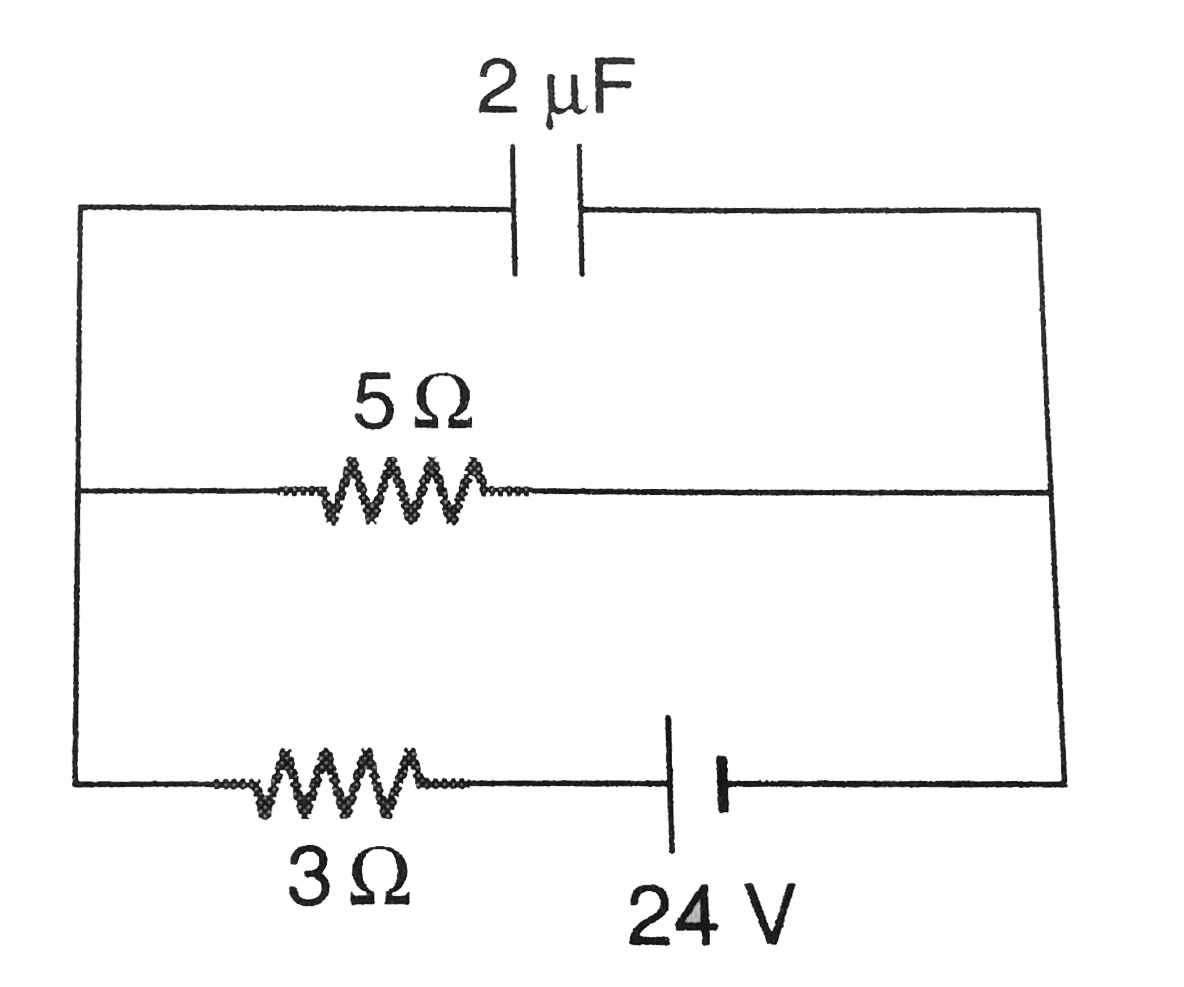
View SolutionFind the charged stored in all the capacitors
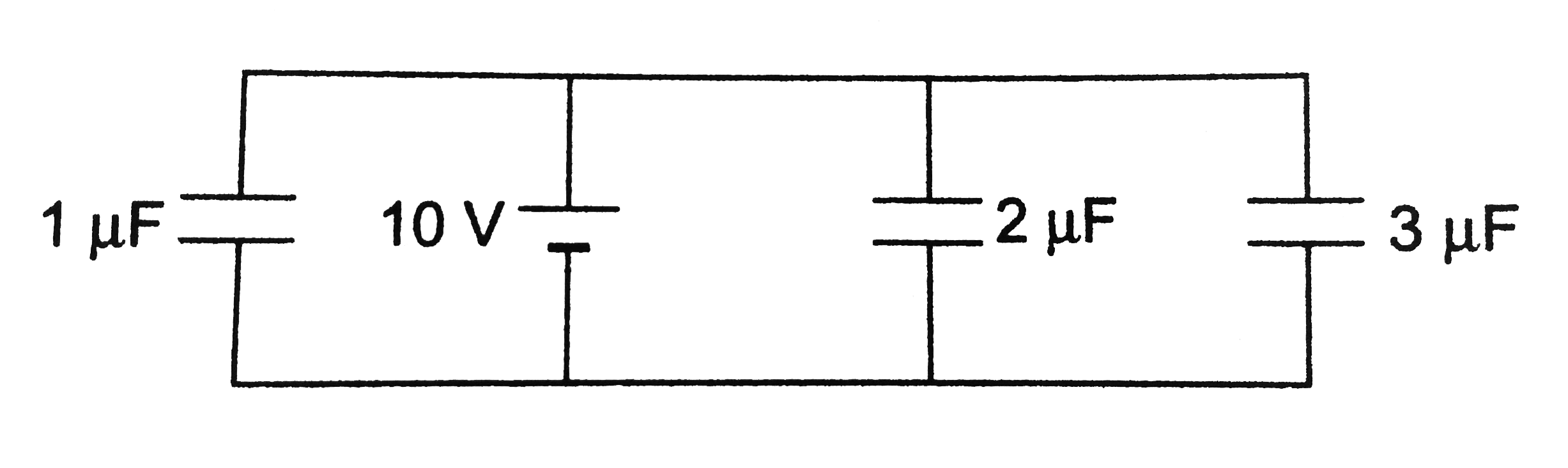
View SolutionThe total electrostatic energy stored in both the capacitor is
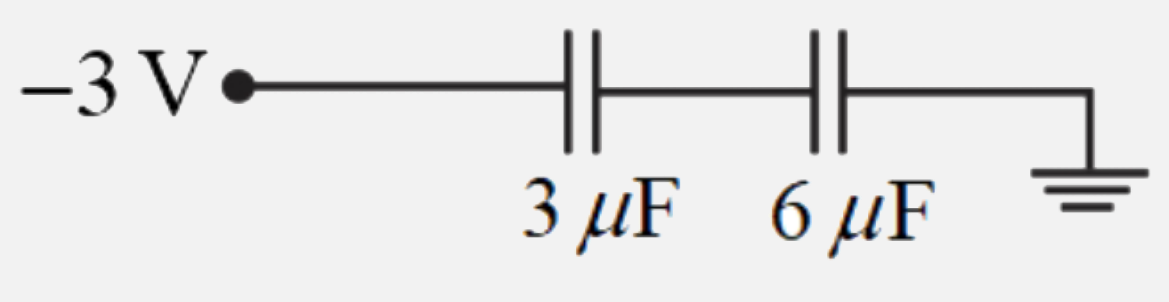
View SolutionThe capacitors shown in figure. Is in steady state. The energy stored in the capacitor is
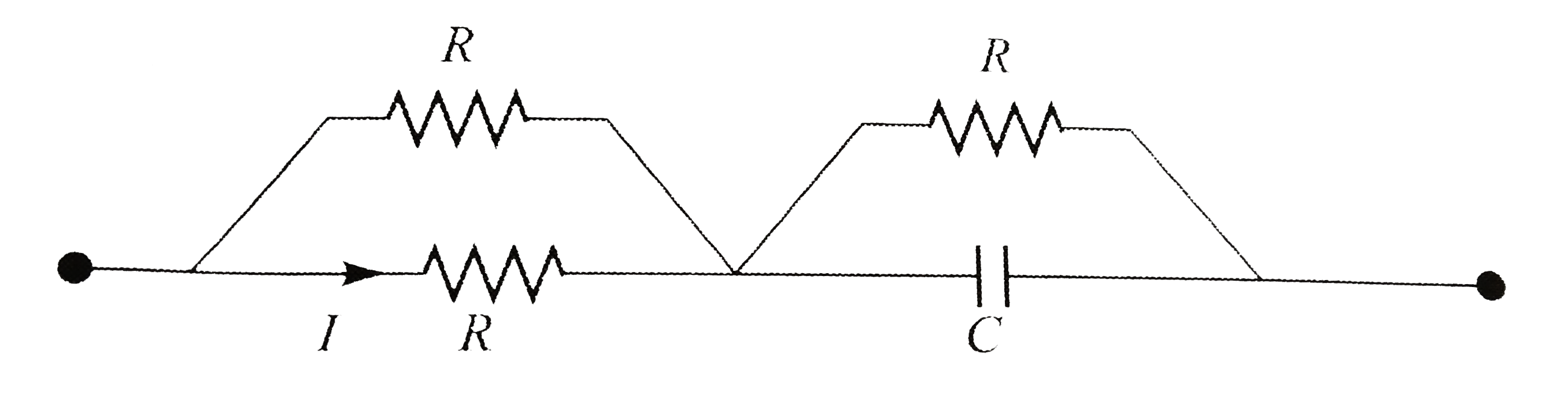
View SolutionAn uncharged capacitor is connected in series with a resistor and a battery. The charging of the capacitor starts at t=0. The rate at which energy stored in the capacitor:-
View SolutionA battery of 10V is connected to a capacitor of capacity 0.lF. The battery is now removed and this capacitor is connected to a second uncharged capacitor. If the charges are distributed equally on these two capacitors, find the total energy stored in the two capacitors. Find the ratio of final energy to initial energy stored in capacitors.
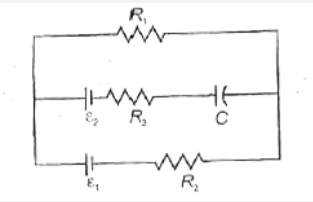
View SolutionFind the charge and energy stored on the capacitor C in the following circuit.
View SolutionThe current in 1Ω resistance and charge stored in the capacitor are
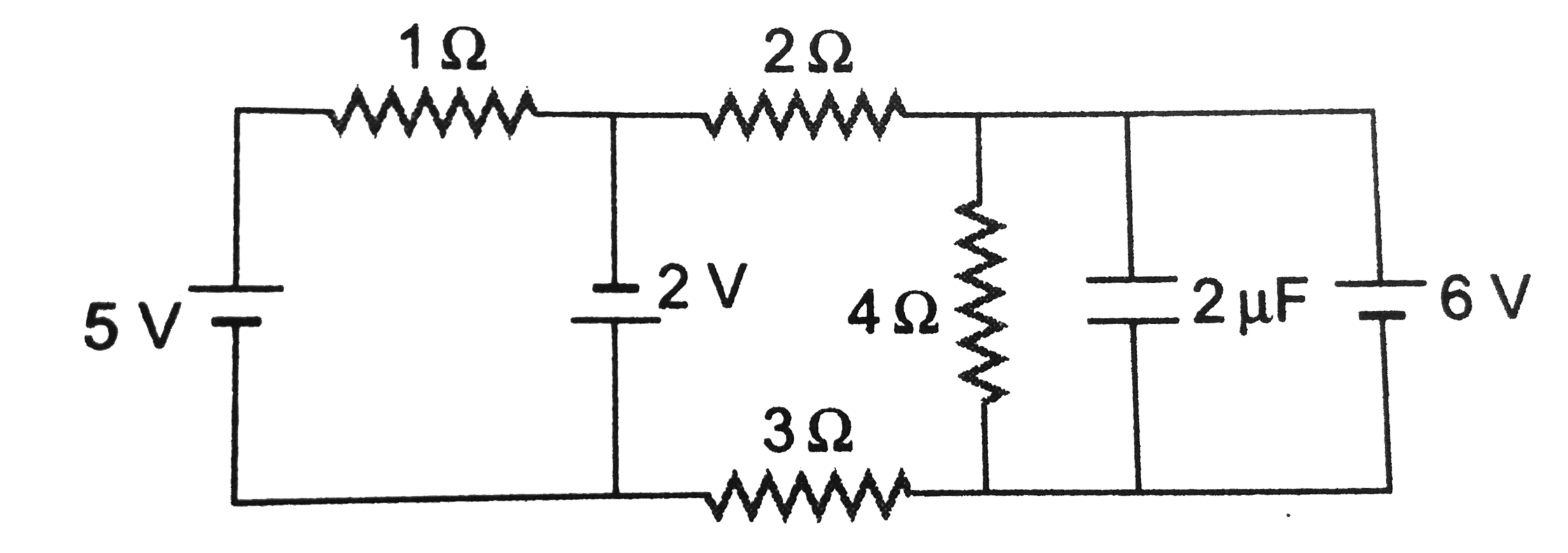
View Solution
