One mole of an ideal monoatomic gas is taken through a polytropic process P2T = constant. The heat required to increase the temperature of the gas by ΔT is
RΔT
3RΔT
5RΔT
6RΔT
The correct Answer is:B
To solve the problem of finding the heat required to increase the temperature of one mole of an ideal monoatomic gas through a polytropic process where P2T is constant, we can follow these steps:
1. Identify the relationship given:
The problem states that P2T=constant. This implies that as pressure P and temperature T change, their relationship remains constant.
2. Use the Ideal Gas Law:
The ideal gas law is given by:
PV=nRT
For one mole of gas (n=1), this simplifies to:
PV=RT
Rearranging gives:
T=PVR
3. Express P2 in terms of T:
From the relationship P2T=constant, we can express P2 as:
P2=constantT
4. Substitute P in terms of T:
Using the ideal gas law, we can express P as:
P=RTV
Substituting this into the equation for P2:
(RTV)2=constantT
5. Determine the work done during the process:
The work done W in a polytropic process is given by:
W=nRΔT1−ηη
where η is the polytropic index. From the relationship P2T=constant, we can find η. Here, we find that η=13.
6. Calculate the work done:
Plugging in n=1 and η=13:
W=1⋅RΔT1−1313=RΔT⋅2313=2RΔT
7. Calculate the change in internal energy:
For a monoatomic ideal gas, the change in internal energy ΔU is given by:
ΔU=32nRΔT=32RΔT
8. Apply the first law of thermodynamics:
The first law states:
Q=ΔU+W
Substituting the expressions for ΔU and W:
Q=32RΔT+2RΔT=(32+2)RΔT=72RΔT
Final Answer:
The heat required to increase the temperature of the gas by ΔT is:
Q=72RΔT
The problem states that P2T=constant. This implies that as pressure P and temperature T change, their relationship remains constant.
The ideal gas law is given by:
PV=nRT
For one mole of gas (n=1), this simplifies to:
PV=RT
Rearranging gives:
T=PVR
From the relationship P2T=constant, we can express P2 as:
P2=constantT
Using the ideal gas law, we can express P as:
P=RTV
Substituting this into the equation for P2:
(RTV)2=constantT
The work done W in a polytropic process is given by:
W=nRΔT1−ηη
where η is the polytropic index. From the relationship P2T=constant, we can find η. Here, we find that η=13.
Plugging in n=1 and η=13:
W=1⋅RΔT1−1313=RΔT⋅2313=2RΔT
For a monoatomic ideal gas, the change in internal energy ΔU is given by:
ΔU=32nRΔT=32RΔT
The first law states:
Q=ΔU+W
Substituting the expressions for ΔU and W:
Q=32RΔT+2RΔT=(32+2)RΔT=72RΔT
The heat required to increase the temperature of the gas by ΔT is:
Q=72RΔT
Similar Questions
One mole of an ideal monoatomic gas is taken through a cyclic process as shown. Choose the correct option(s).
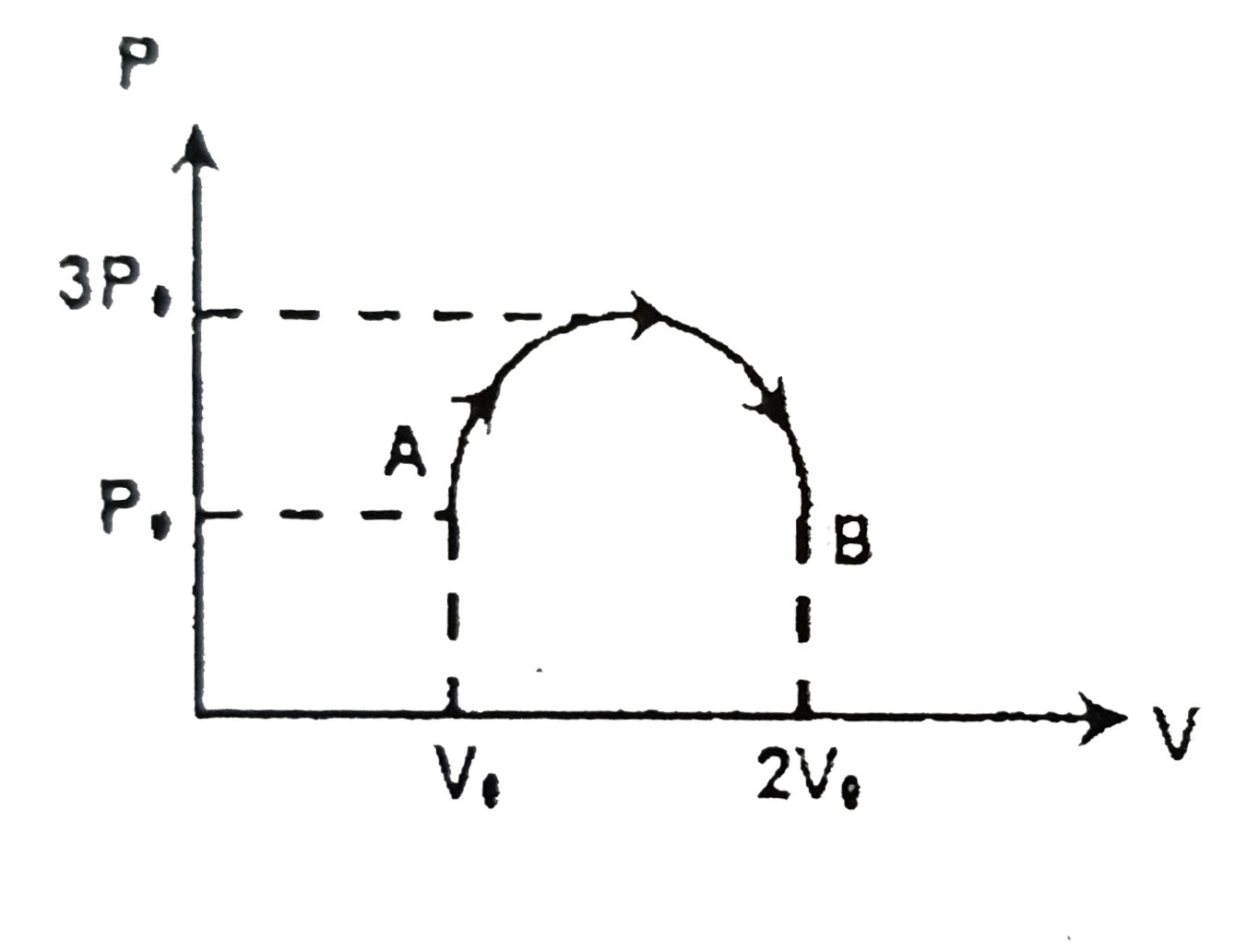
View SolutionOne mole of an ideal monoatomic gas is taken through the thermodynamic process shown in the P−V diagram. The heat supplied to the system is
View SolutionTwo moles of an ideal diatomic gas is taken through a process VT2= constant so that its temperature increases by ΔT=300K. The ratio (ΔUΔQ) of increase in internal energy and heat supplied to the gas during the process is
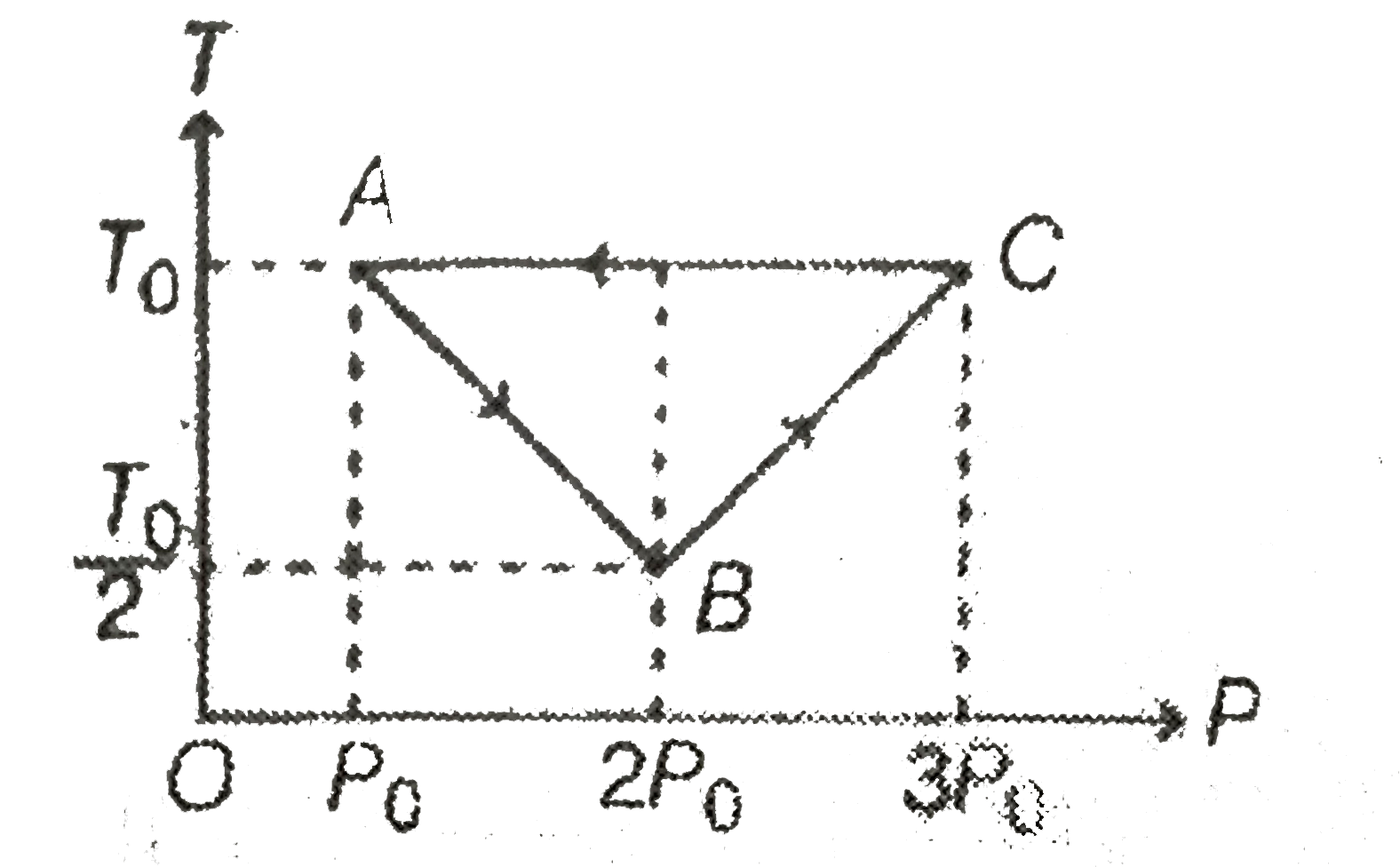
View SolutionOne mole of an ideal monoatomic has is taken through cyclic process ABC as shown in the graph with pressure and temperature as coordinate axes. Process AB is defined as PT = constant. Take universal gas constant to be R. Then:
work done on gas in the process AB is
View SolutionOne mole of an ideal monoatomic has is taken through cyclic process ABC as shown in the graph with pressure and temperature as coordinate axes. Process AB is defined as PT = constant. Take universal gas constant to be R. Then:
Change in internal energy of gas in the process CA is
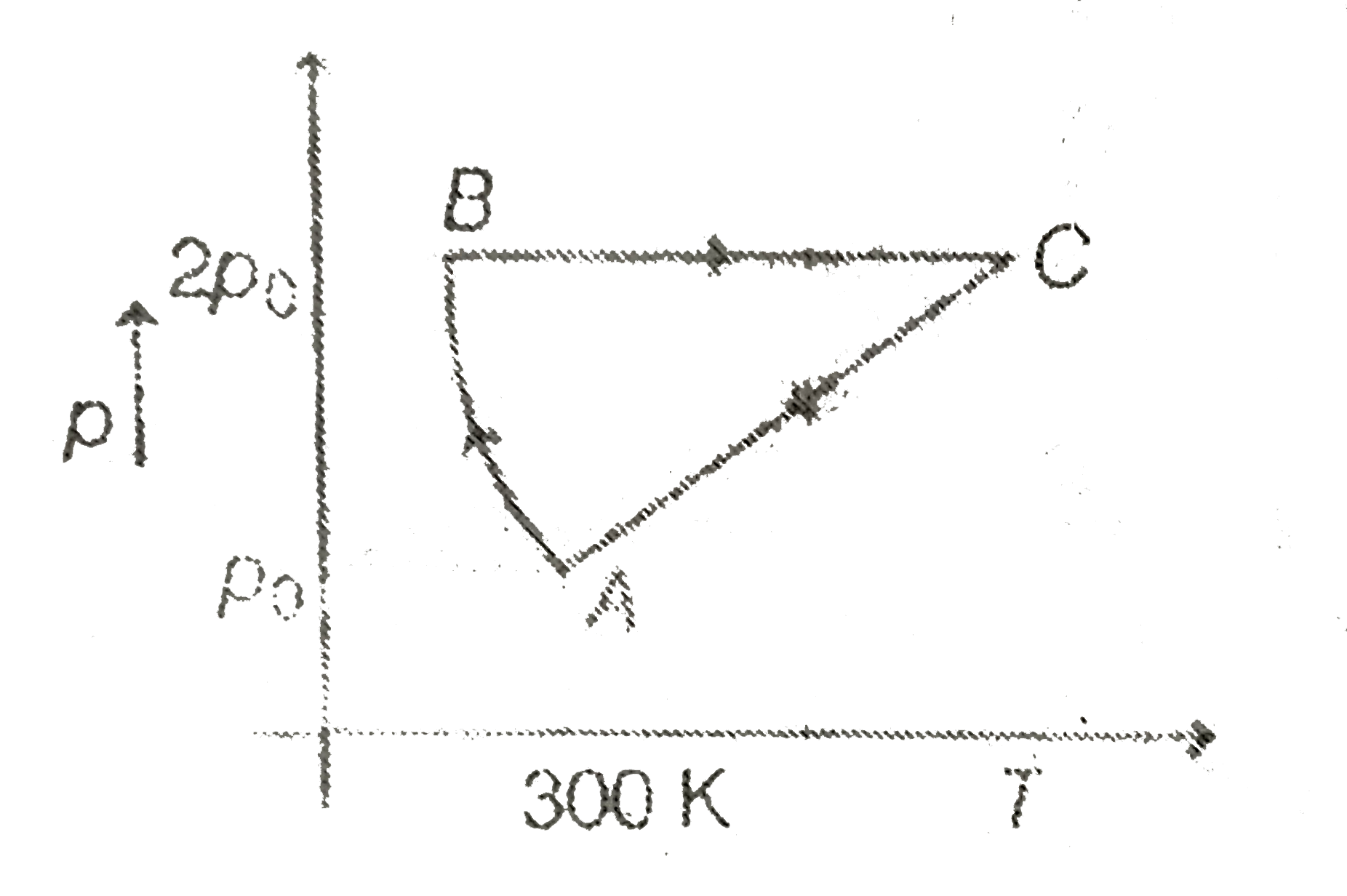
View SolutionTwo moles of an ideal monoatomic gas is taken through a cycle ABCA as shown in the P-T diagram. During the process AB , pressure and temperature of the gas very such that PT=Constant. It T1=300K, calculate
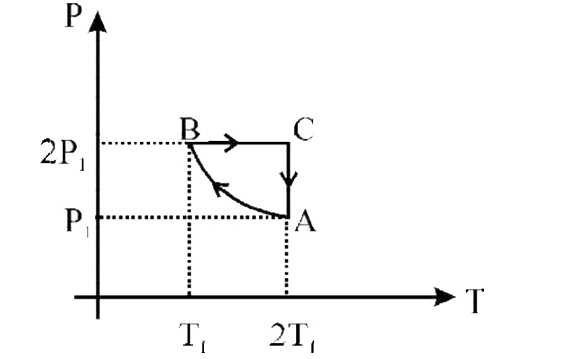
(a) the work done on the gas in the process AB and
(b) the heat absorbed or released by the gas in each of the processes. Give answer in terms of the gas constant R.
View SolutionTwo moles of an ideal monoatomic gas is taken through a cycle ABCA as shown in the P-T diagram. During the process AB , pressure and temperature of the gas very such that PT=Constant. It T1=300K, calculate

(a) the work done on the gas in the process AB and
(b) the heat absorbed or released by the gas in each of the processes. Give answer in terms of the gas constant R.
View SolutionIn a process, temperature and volume of one mole of an ideal monoatomic gas are varied according to the relation VT= K, where K is a constant. In this process the temperataure of the gas is increased by ΔT. The amount of heat absorbed by gas is (R is gas constant).
View SolutionIn a process, temperature and volume of one mole of an ideal monoatomic gas are varied according to the relation VT= K, where K is a constant. In this process the temperataure of the gas is increased by ΔT. The amount of heat absorbed by gas is (R is gas constant).
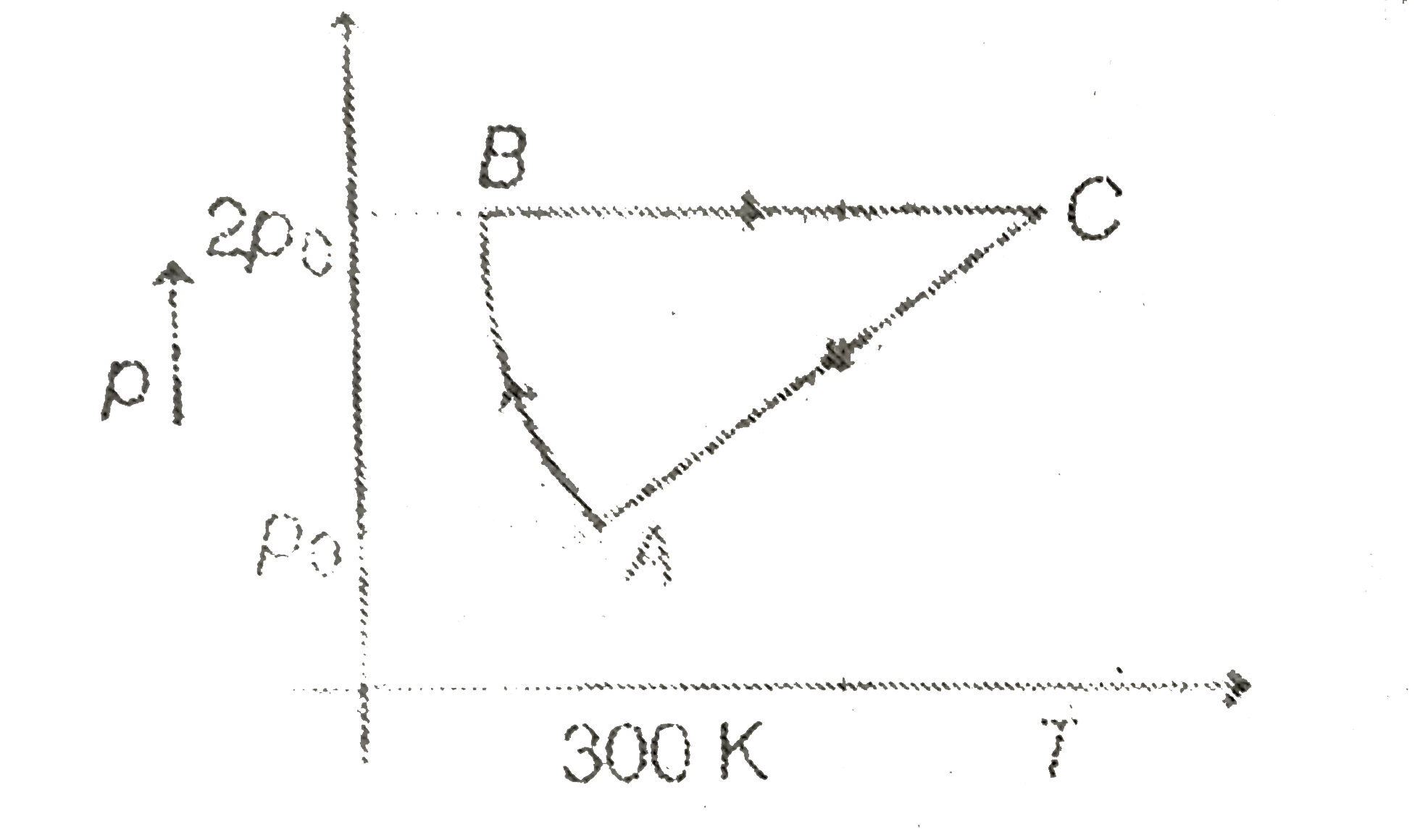
View SolutionTwo moles of an ideal monoatomic gas is taken through a cycle ABCA as shown in the p - T diagram. During the process AB, the pressure and temperature of the gas vary such that pT = constant. If T1=300K and the amount of heat released by the gas during the process AB is Q=−xR, then the value of x is
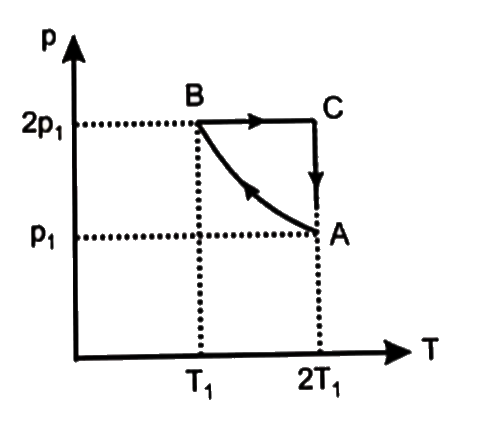
View Solution