Three point charges, each with charge q and mass 'm', are connected by three strings of equal length l whose other end is connected to a fixed point P. They form an equilateral triangle of side 'a' in a horizontal plane. The tension in each string will be
√(mg)2−(q24πε0a2√3)2
mgl√l2−a2/3
3q24πε0a2
none of the above
The correct Answer is:B
To find the tension in each string connecting three point charges arranged in an equilateral triangle, we can follow these steps:
Step 1: Understand the Setup
We have three point charges, each with charge q and mass m, connected by strings of length l to a fixed point P. The charges form an equilateral triangle of side a in a horizontal plane.
Step 2: Analyze the Geometry
Since the strings are of equal length l and connect to a fixed point P, the charges will be at equal heights above the horizontal plane. The angle θ that each string makes with the vertical can be determined using trigonometric relationships.
Step 3: Establish Relationships
Using trigonometry, we can express cosθ and sinθ:
- The horizontal distance from P to the midpoint of the side AC is a2.
- Thus, cosθ=a/2l and sinθ=
⎷1−(a/2l)2.
Step 4: Force Balance in the Vertical Direction
In the vertical direction, the forces acting on each charge are the tension T in the string and the weight mg:
Tsinθ=mg(1)
Step 5: Force Balance in the Horizontal Direction
In the horizontal direction, we consider the electrostatic forces between the charges. The electrostatic force FAC between charges A and C is given by:
FAC=14πϵ0q2a2
The horizontal component of the tension T must balance the net electrostatic force. The angle α between the string and the horizontal plane is 30∘ (since it's an equilateral triangle):
Tcosθcos30∘=FAC+FABsin30∘(2)
Since FAB is equal to FAC, we can simplify this equation.
Step 6: Substitute and Solve
From equation (2), we can express the tension in terms of the electrostatic force:
Tcosθ⋅√32=2⋅14πϵ0q2a2⋅12
This simplifies to:
Tcosθ=14πϵ0q2a2⋅2√3(3)
Step 7: Combine Equations
Now we have two equations:
1. Tsinθ=mg
2. Tcosθ=14πϵ0q2a2⋅2√3
Step 8: Square and Add
Squaring both equations and adding them gives:
T2(sin2θ+cos2θ)=m2g2+(14πϵ0q2a2⋅2√3)2
Using the identity sin2θ+cos2θ=1:
T2=m2g2+(14πϵ0q2a2⋅2√3)2
Step 9: Solve for Tension
Finally, we can express the tension T:
T=
⎷m2g2+(14πϵ0q2a2⋅2√3)2
We have three point charges, each with charge q and mass m, connected by strings of length l to a fixed point P. The charges form an equilateral triangle of side a in a horizontal plane.
Since the strings are of equal length l and connect to a fixed point P, the charges will be at equal heights above the horizontal plane. The angle θ that each string makes with the vertical can be determined using trigonometric relationships.
Using trigonometry, we can express cosθ and sinθ:
- The horizontal distance from P to the midpoint of the side AC is a2.
- Thus, cosθ=a/2l and sinθ=
⎷1−(a/2l)2.
In the vertical direction, the forces acting on each charge are the tension T in the string and the weight mg:
Tsinθ=mg(1)
In the horizontal direction, we consider the electrostatic forces between the charges. The electrostatic force FAC between charges A and C is given by:
FAC=14πϵ0q2a2
The horizontal component of the tension T must balance the net electrostatic force. The angle α between the string and the horizontal plane is 30∘ (since it's an equilateral triangle):
Tcosθcos30∘=FAC+FABsin30∘(2)
Since FAB is equal to FAC, we can simplify this equation.
From equation (2), we can express the tension in terms of the electrostatic force:
Tcosθ⋅√32=2⋅14πϵ0q2a2⋅12
This simplifies to:
Tcosθ=14πϵ0q2a2⋅2√3(3)
Now we have two equations:
1. Tsinθ=mg
2. Tcosθ=14πϵ0q2a2⋅2√3
Squaring both equations and adding them gives:
T2(sin2θ+cos2θ)=m2g2+(14πϵ0q2a2⋅2√3)2
Using the identity sin2θ+cos2θ=1:
T2=m2g2+(14πϵ0q2a2⋅2√3)2
Finally, we can express the tension T:
T=
⎷m2g2+(14πϵ0q2a2⋅2√3)2
Similar Questions
Two particles of mass m and 2m are connected by a string of length L and placed at rest over a smooth horizontal surface. The particles are then given velocities as indicated in the figure shown. The tension developed in the string will be

View SolutionThree points charges of 1C,2Cand3C are placed at the corners of an equilateral triangle of side 100 cm. Find the work done to move these charges to the corners of a similar equilateral triangle of side 50 cm.
View Solution
Knowledge Check
Consider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
Aq24√2πε0l2B−q24πε0l2Cq24πε0l2Dzero
Three points charges of 1C,2Cand3C are placed at the corners of an equilateral triangle of side 100 cm. Find the work done to move these charges to the corners of a similar equilateral triangle of side 50 cm.
View SolutionTwo identical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionThree identical rods, each of mass m and length l, form an equaliteral triangle. Moment of inertia about one of the sides is

View SolutionThree paricles, each of mass m and carrying a charge q each, are suspended from a common pointby insulating massless strings each of length L. If the particles are in equilibrium and are located at the corners of an equilateral triangle of side a, calculate the charge q on each particle. Assume L>>a.
View SolutionThree identical point charges, each of mass m and charge q, hang from three strings as shown in fig. The value of q in term of m, L, and q is
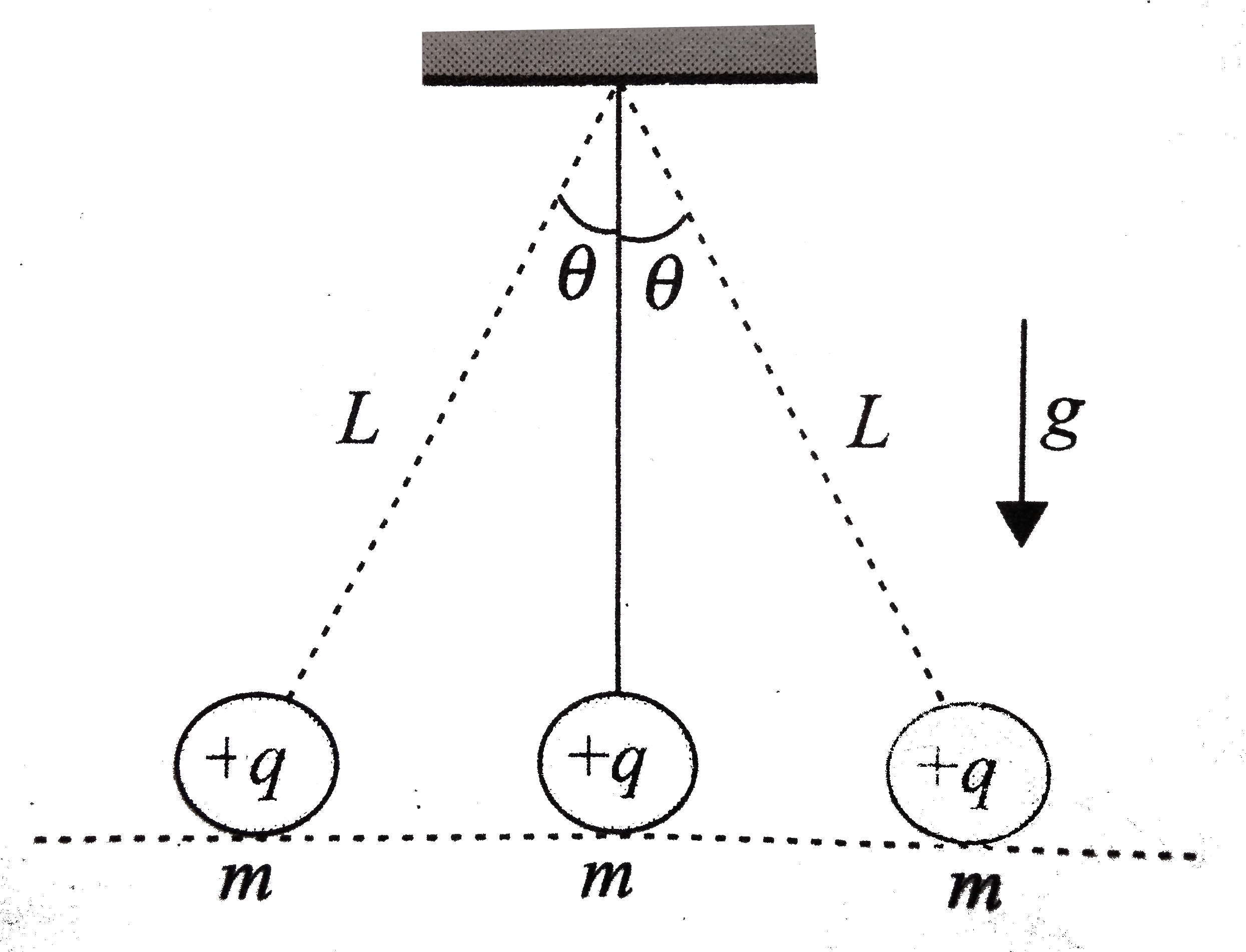
View SolutionTwo indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionThree particle each of mass m are placed at the corners of equilateral triangle of side l

Which of the following is/are correct ?
View Solution
