The gravitational field in a region is given by N/kg, where x and y are in metres. The equipotential lines are plotted as

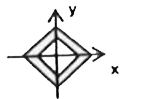


The correct Answer is:A
To find the equipotential lines for the given gravitational field →E=(y^i+x^j) N/kg, we need to understand that equipotential lines are the lines along which the potential energy is constant.
1. Understand the Gravitational Field: The gravitational field is given as →E=(y^i+x^j). This means that the gravitational field has components in both the x and y directions, which depend on the coordinates x and y.
2. Relate Gravitational Field to Potential: The gravitational potential V is related to the gravitational field →E by the equation:
→E=−∇V
This means that the components of the gravitational field can be expressed as:
Ex=−∂V∂xandEy=−∂V∂y
3. Set Up the Equations: From the given field, we have:
Ex=yandEy=x
Therefore, we can write:
−∂V∂x=y(1)
−∂V∂y=x(2)
4. Integrate Equation (1): To find V, we can integrate equation (1) with respect to x:
V=−∫ydx=−yx+f(y)
where f(y) is an arbitrary function of y.
5. Differentiate with respect to y: Now, we differentiate V with respect to y and set it equal to equation (2):
∂V∂y=−x+f′(y)
Setting this equal to −x gives:
−x+f′(y)=−x
This implies that f′(y)=0, so f(y) is a constant. Thus, we can write:
V=−yx+C
where C is a constant.
6. Equipotential Lines: The equipotential lines are given by setting V to a constant value V0:
−yx+C=V0
Rearranging gives:
yx=C−V0
This equation represents hyperbolas in the xy-plane.
Final Result:
The equipotential lines are given by the equation:
yx=constant
→E=−∇V
This means that the components of the gravitational field can be expressed as:
Ex=−∂V∂xandEy=−∂V∂y
Ex=yandEy=x
Therefore, we can write:
−∂V∂x=y(1)
−∂V∂y=x(2)
V=−∫ydx=−yx+f(y)
where f(y) is an arbitrary function of y.
∂V∂y=−x+f′(y)
Setting this equal to −x gives:
−x+f′(y)=−x
This implies that f′(y)=0, so f(y) is a constant. Thus, we can write:
V=−yx+C
where C is a constant.
−yx+C=V0
Rearranging gives:
yx=C−V0
This equation represents hyperbolas in the xy-plane.
The equipotential lines are given by the equation:
yx=constant
Similar Questions
Electrostatic field in a region is given by , vecE= (yzhati + zxhatj + xyhatk)V/m , where x,y and z are in m. If electric potential at origin is zero, then potential at (1m,1m, 1m) is
View SolutionThe gravitational field in a region is given by →E=(5ˆi+12ˆj)N/Kg. The change in gravitational potential energy if a particle of mass 1 kg is taken from the origin to the point (12m, 5m).
View SolutionThe gravitational field in a region is given by →g=(5ˆi+12ˆj)N kg−1. The change in the gravitational potential energy of a particle of mass 2kg when it is taken from the origin to a point (7m,−3m) is
View SolutionThe gravitational field in a region is given by E=(2ˆi+3ˆj)N/kg.
Find the work done by the gravitational filed when a particle of mass 1kg is moved on the line 3y+2X=5 from (1m,1m) to (−2m,3m).
View SolutionThe gravitational field in a region is given by →E=(3ˆi−4ˆj)Nkg−1. Find out the work done (in joule) in displacing a particle by 1m along the line 4y=3x+9.
View SolutionThe gravitational field in a region is given by →E=(3ˆi−4ˆj)Nkg−1. Find out the work done (in joule) in displacing a particle by 1m along the line 4y=3x+9.
View SolutionThe gravitational field in a in region is given by →g=(4ˆi+→j)N/kg. What done by this field is zero when the particle is moved along the line :
View SolutionThe gravitational field in a region is given by →E=(4ˆi+3ˆj)N/Kg. The gravitational potential at the points (3m, 0) and (0, 4m). If the potential at the origin is taken to be zero.
View SolutionThe gravitational field in a region is given by →g=(2ˆi+3ˆj) N/kg. The work done in moving a particle of mass 1 kg from (1, 1) to (2,13) along the line 3y + 2x = 5 is
View SolutionThe gravitational field in a region is given by →E=−(20Nkg−1)(ˆi+ˆj). Find the gravitational potential at the origin (0,0) in Jkg−1
View Solution
