Electrostatic field in a region is given by , vecE= (yzhati + zxhatj + xyhatk)V/m , where x,y and z are in m. If electric potential at origin is zero, then potential at (1m,1m, 1m) is
−1V
1V
−3V
3V
To find the electric potential at the point (1 m, 1 m, 1 m) given the electric field →E=(yz^i+zx^j+xy^k)V/m and that the potential at the origin is zero, we can follow these steps:
Step 1: Write the expression for the electric potential
The relationship between electric field →E and electric potential V is given by:
dV=−→E⋅d→r
where d→r=(dx^i+dy^j+dz^k).
Step 2: Calculate the dot product →E⋅d→r
Substituting the expression for →E:
→E=(yz^i+zx^j+xy^k)
The dot product becomes:
→E⋅d→r=(yz^i+zx^j+xy^k)⋅(dx^i+dy^j+dz^k)=yzdx+zxdy+xydz
Thus,
dV=−(yzdx+zxdy+xydz)
Step 3: Set up the integral for potential
To find the potential V at the point (1, 1, 1), we need to integrate from the origin (0, 0, 0) to (1, 1, 1):
V(1,1,1)−V(0,0,0)=−∫10(yzdx+zxdy+xydz)
Since V(0,0,0)=0, we have:
V(1,1,1)=−∫10(yzdx+zxdy+xydz)
Step 4: Evaluate the integral
We will evaluate the integral by breaking it into three parts. We will integrate each term separately.
1. Integrating yzdx:
- Here, y and z are constants when integrating with respect to x.
- The limits for x are from 0 to 1.
- Thus, the integral becomes:
−∫10yzdx=−yz⋅(1−0)=−yz
2. Integrating zxdy:
- Here, z and x are constants when integrating with respect to y.
- The limits for y are from 0 to 1.
- Thus, the integral becomes:
−∫10zxdy=−zx⋅(1−0)=−zx
3. Integrating xydz:
- Here, x and y are constants when integrating with respect to z.
- The limits for z are from 0 to 1.
- Thus, the integral becomes:
−∫10xydz=−xy⋅(1−0)=−xy
Step 5: Combine the results
Now, substituting x=1, y=1, and z=1 into the results:
V(1,1,1)=−(−yz−zx−xy)=−(−1⋅1−1⋅1−1⋅1)=−(−1−1−1)=−(−3)=−3
Step 6: Final result
Thus, the potential at the point (1 m, 1 m, 1 m) is:
V(1,1,1)=−3V
The relationship between electric field →E and electric potential V is given by:
dV=−→E⋅d→r
where d→r=(dx^i+dy^j+dz^k).
Substituting the expression for →E:
→E=(yz^i+zx^j+xy^k)
The dot product becomes:
→E⋅d→r=(yz^i+zx^j+xy^k)⋅(dx^i+dy^j+dz^k)=yzdx+zxdy+xydz
Thus,
dV=−(yzdx+zxdy+xydz)
To find the potential V at the point (1, 1, 1), we need to integrate from the origin (0, 0, 0) to (1, 1, 1):
V(1,1,1)−V(0,0,0)=−∫10(yzdx+zxdy+xydz)
Since V(0,0,0)=0, we have:
V(1,1,1)=−∫10(yzdx+zxdy+xydz)
We will evaluate the integral by breaking it into three parts. We will integrate each term separately.
- Here, y and z are constants when integrating with respect to x.
- The limits for x are from 0 to 1.
- Thus, the integral becomes:
−∫10yzdx=−yz⋅(1−0)=−yz
- Here, z and x are constants when integrating with respect to y.
- The limits for y are from 0 to 1.
- Thus, the integral becomes:
−∫10zxdy=−zx⋅(1−0)=−zx
- Here, x and y are constants when integrating with respect to z.
- The limits for z are from 0 to 1.
- Thus, the integral becomes:
−∫10xydz=−xy⋅(1−0)=−xy
Now, substituting x=1, y=1, and z=1 into the results:
V(1,1,1)=−(−yz−zx−xy)=−(−1⋅1−1⋅1−1⋅1)=−(−1−1−1)=−(−3)=−3
Thus, the potential at the point (1 m, 1 m, 1 m) is:
V(1,1,1)=−3V
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE21videos
TEST 1
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Try Yourself63videos
SYSTEM OF PARTICLES AND ROTATIONAL MOTION
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 2EXERCISE - Exercise308videos
TEST 2
Similar Questions
An electric field E=(20ˆi+30ˆj) N/C exists in the space. If the potential at the origin is taken be zero, find the potential at (2m,2m).
View SolutionThe electric field in a region is given by →E=(Ax3)ˆi. Write a suitable SI unit for A. Write an expression for the potential in the region assuming the potential at infinity to be zero.
View SolutionAn electric field E=(20ˆi+30ˆj) N/C exists in the space. If thepotential at the origin is taken be zero, find the potential at (2m,2m).
View SolutionThe gravitational field in a region is given by →E=(4ˆi+3ˆj)N/Kg. The gravitational potential at the points (3m, 0) and (0, 4m). If the potential at the origin is taken to be zero.
View SolutionElectric field in a region is given by E=(2ˆi+3ˆj−4ˆk)V/m. Find the potential difference between points (0, 0, 0) and (1,2,3) in this region.
View SolutionThe gravitational field in a region is given by →E=−(20Nkg−1)(ˆi+ˆj). Find the gravitational potential at the origin (0,0) in Jkg−1
View SolutionThe electric field in a region is given by →E=(Ax3)→I. Write a suitable SI unit for A. Write an experssion for. the potential in the region assuming the potential at. infinity to be zero.
View SolutionAn electric field →E=−−−−−−−→i20+→j30NC−1 exists in the space. If the potential at the origin is taken to be zero find the potential at (2m, 2m).
View SolutionThe electric field in a certain region is given by E=(5ˆi−3ˆj)kV/m. Find the difference in potential VB−VA. If A is at the origin and point B is at a. (0,0,5)m, b. (4,0,3) m.
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in figure. The y−andz−compo≠nts of the electric field are zero in this region. If the electric potential is 10 V at the origin, then the potential at x = 2.0 m is
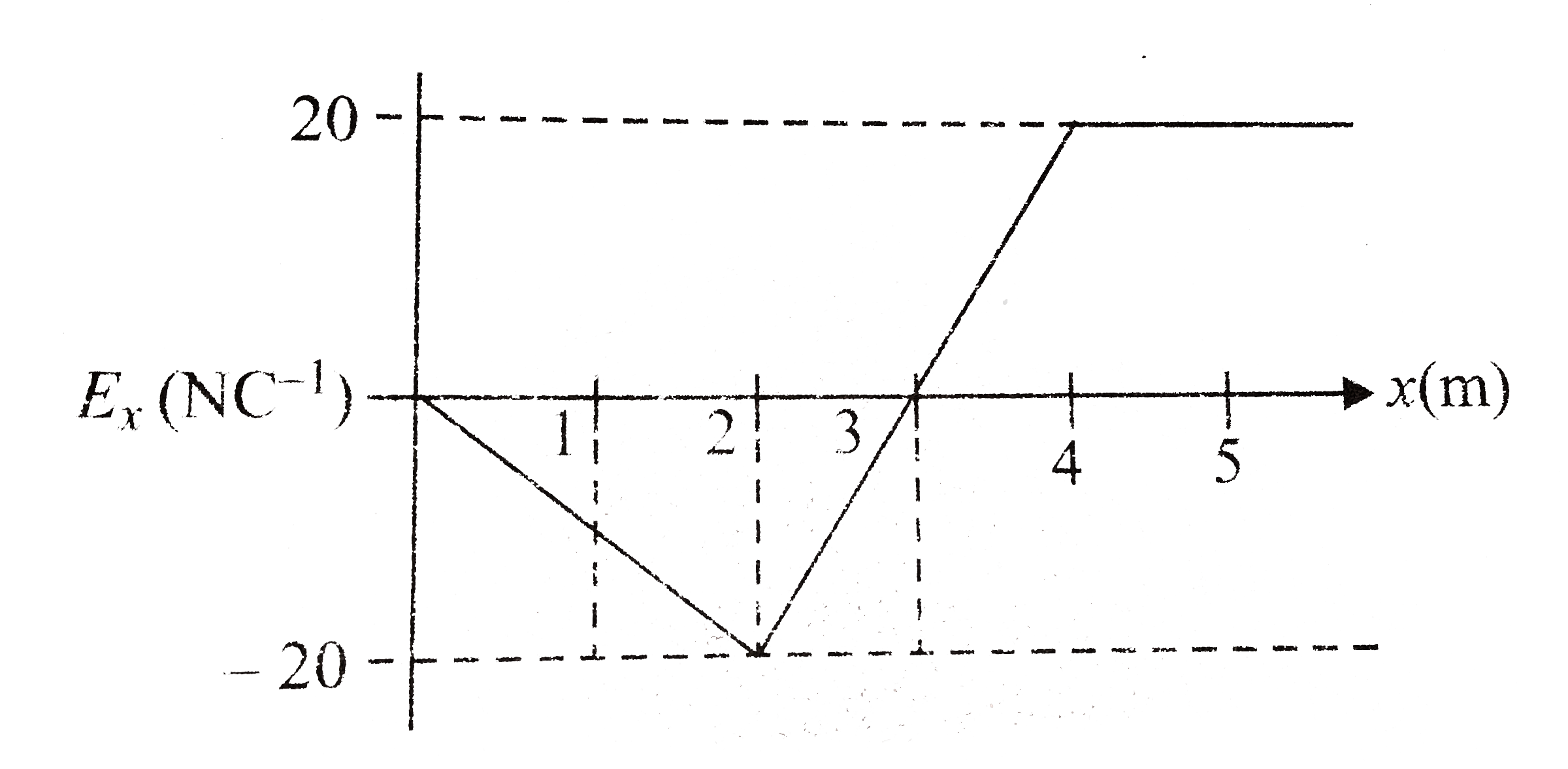 View Solution
View Solution

