A wall has two layers A and B made of two different materials thermal conductivities KA and KB (KA=3KB). The thickness of both the layers is same. The temperature across the wall is 20∘C in thermal equilibrium. Then
temperature difference across A is 12∘C
rate of heat transfer across A is more than that across B
rate of heat transfer is same for both
temperature difference across A is 15∘C
The correct Answer is:C
To solve the problem, we need to analyze the heat transfer through the two layers of the wall. Here are the steps to arrive at the solution:
Step 1: Understand the Setup
We have two layers A and B with thermal conductivities KA and KB respectively. We know that KA=3KB. The thickness of both layers is the same, and the temperature difference across the wall is 20∘C.
Step 2: Define the Temperatures
Let:
- T1 be the temperature on one side of the wall.
- T2 be the temperature on the other side of the wall.
- T be the temperature at the interface between the two layers.
Given that T1−T2=20∘C, we can express T2 as:
T2=T1−20
Step 3: Write the Heat Transfer Equations
Since the layers are in series, the heat transfer (or heat current) through both layers must be equal. The heat transfer rate H can be expressed as:
H=T1−TRA=T−T2RB
where RA and RB are the thermal resistances of layers A and B respectively.
Step 4: Calculate the Thermal Resistances
The thermal resistance for each layer can be defined as:
RA=LKA⋅A
RB=LKB⋅A
where L is the thickness of the layers and A is the cross-sectional area (which we can assume to be the same for both layers).
Step 5: Substitute the Resistances into the Heat Transfer Equation
Substituting the resistances into the heat transfer equations gives:
H=T1−TLKA⋅A=KA⋅A(T1−T)L
H=T−T2LKB⋅A=KB⋅A(T−T2)L
Step 6: Set the Heat Transfer Equations Equal
Setting the two equations for H equal to each other:
KA(T1−T)=KB(T−T2)
Step 7: Substitute KA and T2
Substituting KA=3KB and T2=T1−20:
3KB(T1−T)=KB(T−(T1−20))
Canceling KB (assuming KB≠0):
3(T1−T)=T−T1+20
Step 8: Rearranging the Equation
Rearranging gives:
3T1−3T=T−T1+20
4T1−4T=20
T1−T=5
Step 9: Conclusion
Thus, the temperature difference across layer A is:
T1−T=5∘C
We have two layers A and B with thermal conductivities KA and KB respectively. We know that KA=3KB. The thickness of both layers is the same, and the temperature difference across the wall is 20∘C.
Let:
- T1 be the temperature on one side of the wall.
- T2 be the temperature on the other side of the wall.
- T be the temperature at the interface between the two layers.
T2=T1−20
Since the layers are in series, the heat transfer (or heat current) through both layers must be equal. The heat transfer rate H can be expressed as:
H=T1−TRA=T−T2RB
where RA and RB are the thermal resistances of layers A and B respectively.
The thermal resistance for each layer can be defined as:
RA=LKA⋅A
RB=LKB⋅A
where L is the thickness of the layers and A is the cross-sectional area (which we can assume to be the same for both layers).
Substituting the resistances into the heat transfer equations gives:
H=T1−TLKA⋅A=KA⋅A(T1−T)L
H=T−T2LKB⋅A=KB⋅A(T−T2)L
Setting the two equations for H equal to each other:
KA(T1−T)=KB(T−T2)
Substituting KA=3KB and T2=T1−20:
3KB(T1−T)=KB(T−(T1−20))
Canceling KB (assuming KB≠0):
3(T1−T)=T−T1+20
Rearranging gives:
3T1−3T=T−T1+20
4T1−4T=20
T1−T=5
Thus, the temperature difference across layer A is:
T1−T=5∘C
Similar Questions
when two bodies A and B are in thermal equilibrium then
View SolutionA wall has two layers X and Y each made of different materials. Both layers have same thickness. Thermal conductivity of X is twice that of Y. At steady state the temperature difference of opposite faces of wall is 54°C. The temperature difference across Y layer is
View Solution
Knowledge Check
A wall has two layers A and B, each made of different materials. Both the layers have the same thickness. The thermal conductivity of the material of A is twice that of B. Under thermal equilibrium , the temperature differeence across the wall is 36∘C. The temperature difference across the layer A is
A6∘CB12∘CC18∘CD24∘CA wall has two layers A and B, each made of different material. Both the layers have the same thickness. The thermal conductivity of the material of A is twice that of B . Under thermal equilibrium, the temperature difference across the wall is 36∘C. The temperature difference across the layer A is
A12.∘CB18.∘CC6.∘CD24.∘C
A wall has two layers A and B, each made of different material. Both the layers have the same thickness. The thermal conductivity of the material of A is twice that of B . Under thermal equilibrium, the temperature difference across the wall is 36∘C. The temperature difference across the layer A is
View SolutionA wall has two layers A and B each made of different materials. The layer A is 10cm thick and B is 20 cm thick. The thermal conductivity of A is thrice that of B. Under thermal equilibrium temperature difference across the wall is 35∘C. The difference of temperature across the layer A is
View SolutionA composite slab is made of two parallel layers of two different materials of thermal conductivities K1andK2 are of same thickness. Show that the equivalent thermal conductivity of the slab is 2K1K2K1+K2
View SolutionTwo identical rods are made of different materials whose thermal conductivities are K1andK2. They are placed end to end between two heat reservoirs at temperatures θ1andθ2. The temperature of the junction of the rod is

View SolutionThe wall of a house is made of two different materials of same thickness. The temperatures of the outer wall is T2 and that of inner wall is T1<T2. The temperature variation inside the wall as shown in the figure. Then :
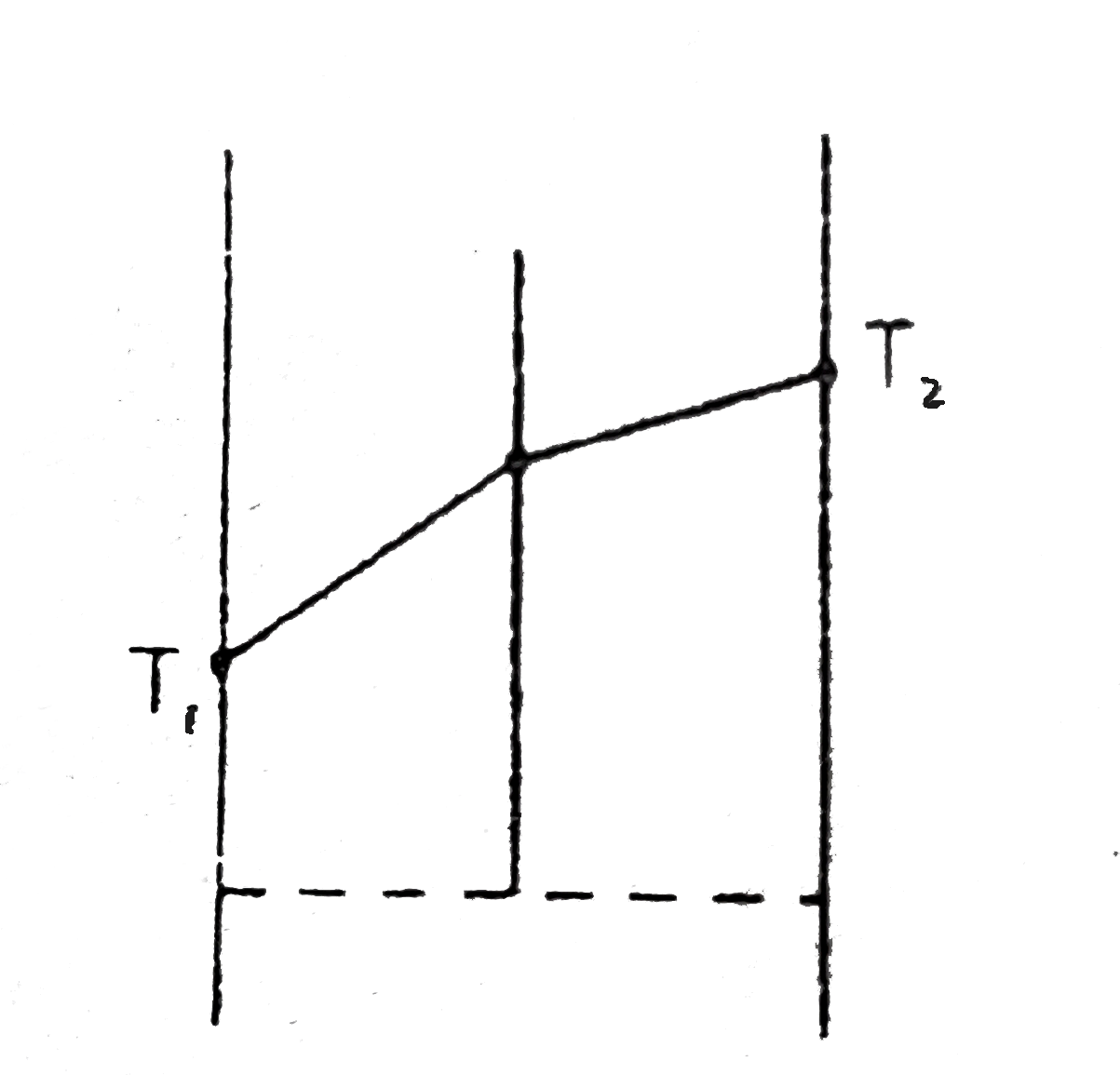
View SolutionA slab consists of two layers of different materials of the same thickness and having thermal conductivities K1 and K2. The equivalent thermal conductivity of the slab is
View Solution
