A current carrying circular loop of radius 50 mm, made of a very thin wire has inductance 0.26 μH and is placed in the uniform magnetic field 0,5 mT. The plane of the loop is perpendicular to the magnetic field lines. The resistance of loop can be neglected. Now the magnetic field has been turned off. Find the current in the loop (approximately)
30A
15 A
10A
0A
The correct Answer is:B
To find the induced current in a circular loop when the magnetic field is turned off, we can use the relationship between magnetic flux, inductance, and current. Here’s a step-by-step solution:
Step 1: Understand the Given Information
- Radius of the loop (R) = 50 mm = 0.05 m
- Inductance (L) = 0.26 µH = 0.26 × 10⁻⁶ H
- Magnetic field (B) = 0.5 mT = 0.5 × 10⁻³ T
- The resistance of the loop can be neglected.
Step 2: Calculate the Area of the Loop
The area (A) of a circular loop is given by the formula:
A=πR2
Substituting the radius:
A=π(0.05)2=π(0.0025)≈0.007854 m2
Step 3: Calculate the Magnetic Flux (Φ)
The magnetic flux (Φ) through the loop is given by:
Φ=B⋅A
Substituting the values:
Φ=(0.5×10−3)⋅(0.007854)≈3.927×10−6 Wb
Step 4: Relate Inductance, Current, and Magnetic Flux
The relationship between inductance (L), current (I), and magnetic flux (Φ) is given by:
Φ=L⋅I
Rearranging this to find the current:
I=ΦL
Step 5: Substitute the Values to Find Current
Substituting the values of Φ and L:
I=3.927×10−60.26×10−6≈15.096 A
Step 6: Round the Answer
The current can be approximated to:
I≈15 A
Final Answer
The induced current in the loop when the magnetic field is turned off is approximately 15 A.
---
- Radius of the loop (R) = 50 mm = 0.05 m
- Inductance (L) = 0.26 µH = 0.26 × 10⁻⁶ H
- Magnetic field (B) = 0.5 mT = 0.5 × 10⁻³ T
- The resistance of the loop can be neglected.
The area (A) of a circular loop is given by the formula:
A=πR2
Substituting the radius:
A=π(0.05)2=π(0.0025)≈0.007854 m2
The magnetic flux (Φ) through the loop is given by:
Φ=B⋅A
Substituting the values:
Φ=(0.5×10−3)⋅(0.007854)≈3.927×10−6 Wb
The relationship between inductance (L), current (I), and magnetic flux (Φ) is given by:
Φ=L⋅I
Rearranging this to find the current:
I=ΦL
Substituting the values of Φ and L:
I=3.927×10−60.26×10−6≈15.096 A
The current can be approximated to:
I≈15 A
The induced current in the loop when the magnetic field is turned off is approximately 15 A.
Similar Questions
In the figure shown a semicircular wire loop is placed in a uniform magnetic field B=1.0T. The plane of the loop is perpendicular to the magnetic field. Current i=2A flows in the loop in the directions shown. Find the magnitude of the magnetic force in both the cases a and b. The radius of the loop is 1.0 m
 View Solution
View SolutionIn the figure shown a semicircular wire loop is placed in a uniform magnetic field B=1.0T. The plane of the loop is perpendicular to the magnetic field. Current i=2A flows in the loop in the directions shown. Find the magnitude of the magnetic force in both the cases a and b. The radius of the loop is 1.0 m
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
AI r BB2πrIBCzeroDπrIB
A loop of Irregular shape made of flexible conducting wire carrying clockwise current is placed in uniform inward magnetic field, such that its plane is perpendicular to the field. Then the loop
View SolutionA circular loop of radius a, carrying a current I, is placed in a tow dimensional magnetic field. The centre of the loop coincides with the centre of the filed The strenght of the magnetic field at the pariphery of the loop is B. find the magnetic force on the wire.
 View Solution
View SolutionA conducting circular loop of radiius r carries a constant current i. It is placed in a uniform magnetic field →B0 such that →B0 is perpendicular to the plane of the loop . The magnetic force acting on the loop is
View SolutionA circular loop of area 1cm2 , carrying a current of 10 A , is placed in a magnetic field of 0.1 T perpendicular to the plane of the loop. The torque on the loop due to the magnetic field is
View SolutionIn non-uniform magnetic field in certain direction, current loop is placed
View SolutionA semi circular current loop is placed in an uniform magnetic field of 1 tesla as shown. If the radius of loop is 1 m, the magnetic force on the loop is
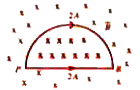 View Solution
View SolutionWhat will be magnetic field at centre of current carrying circular loop of radius R?
View Solution
