For a wave propagating in the positive x direction the instantaneous displacement of the particle is y=Asin2πT(t−xv). What is the significance of the negative sign ? If positive sign is used, what does it represent?
To solve the question regarding the significance of the negative sign in the wave equation y=Asin(2πT(t−xv)), we can break it down into a series of steps:
Step 1: Understand the Wave Equation
The given wave equation describes a wave propagating in the positive x-direction. The general form of a wave can be written as:
y=Asin(kx−ωt)
where k is the wave number and ω is the angular frequency.
Step 2: Identify the Variables
In the equation y=Asin(2πT(t−xv)):
- A is the amplitude of the wave.
- T is the period of the wave.
- v is the wave speed.
- The term (t−xv) represents the phase of the wave.
Step 3: Analyze the Significance of the Negative Sign
The negative sign in the term (t−xv) indicates that as time t increases, the position x must also increase for the phase to remain constant. This means that the wave is moving in the positive x-direction.
Step 4: Consider the Positive Sign Scenario
If we replace the negative sign with a positive sign, the equation would be:
y=Asin(2πT(t+xv))
In this case, the phase becomes (t+xv). For the phase to remain constant as time t increases, x must decrease. This indicates that the wave is moving in the negative x-direction.
Step 5: Conclusion
The negative sign in the wave equation signifies that the wave is propagating in the positive x-direction, while a positive sign would indicate propagation in the negative x-direction.
The given wave equation describes a wave propagating in the positive x-direction. The general form of a wave can be written as:
y=Asin(kx−ωt)
where k is the wave number and ω is the angular frequency.
In the equation y=Asin(2πT(t−xv)):
- A is the amplitude of the wave.
- T is the period of the wave.
- v is the wave speed.
- The term (t−xv) represents the phase of the wave.
The negative sign in the term (t−xv) indicates that as time t increases, the position x must also increase for the phase to remain constant. This means that the wave is moving in the positive x-direction.
If we replace the negative sign with a positive sign, the equation would be:
y=Asin(2πT(t+xv))
In this case, the phase becomes (t+xv). For the phase to remain constant as time t increases, x must decrease. This indicates that the wave is moving in the negative x-direction.
The negative sign in the wave equation signifies that the wave is propagating in the positive x-direction, while a positive sign would indicate propagation in the negative x-direction.
Topper's Solved these Questions
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - Superposition Of Waves, Beats, Stationary Waves
55 Videos
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - Doppler Effect, Musical, Sound, Noise
26 Videos
- WAVESBOOK - ICSECHAPTER - WAVESEXERCISE - Long Answer Questions
16 Videos
- VECTORS SCALARS ELEMENTARY CALCULUS BOOK - ICSECHAPTER - VECTORS SCALARS ELEMENTARY CALCULUS EXERCISE - UNSOLVED PROBLEMS
79 Videos
Similar Questions
A wave is propagating in positive x−direction. A time t=0 its snapshot is taken as shown. If the wave equation is y=Asin(ωt−Kx+ϕ), then ϕ is
_2019_CBT7_E01_013_Q01.png)
View SolutionA wave is propagating in positive x−direction. A time t=0 its snapshot is taken as shown. If the wave equation is y=Asin(ωt−Kx+ϕ), then ϕ is
_2019_CBT7_E01_013_Q01.png)
View SolutionWhat will be the sign of the product if we multiply:
five positive and seven negative integers?
View SolutionThe displacement of a particle is given by x=3sin(5πt)+4cos(5πt). The amplitude of particle is
View SolutionWhat will be the sign of the product if we multiply:
six positive and eight negative integers?
View SolutionA wave propagates in a string in the positive x-direction with velocity v. The shape of the string at t=t0 is given by
f(x,t0)=Asin(x2a2). Then the wave equation at any instant t is given by
View SolutionState whether the potential is a scalar or vector ? What does the positive and negative sign of potential convey ?
View SolutionThe velocity of a particle moving in the positive direction of X-axis varies as v=5√x. Assuming that at t = 0, particle was at x = 0. What is the acceleration of the particle ?
View Solutionx−t graph of a particle in SHM is
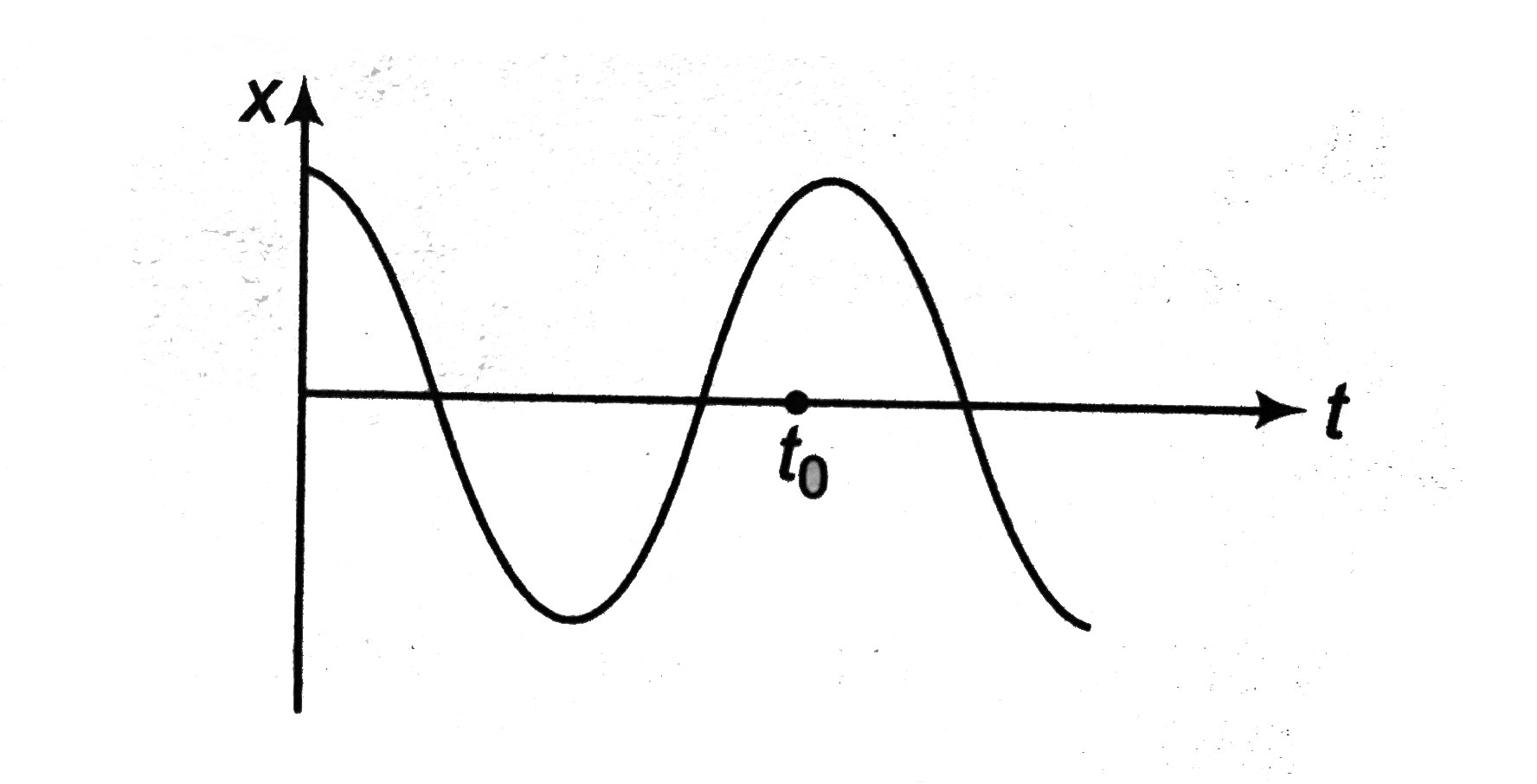
At time t=t0, what are the signs of v and a of the particle?
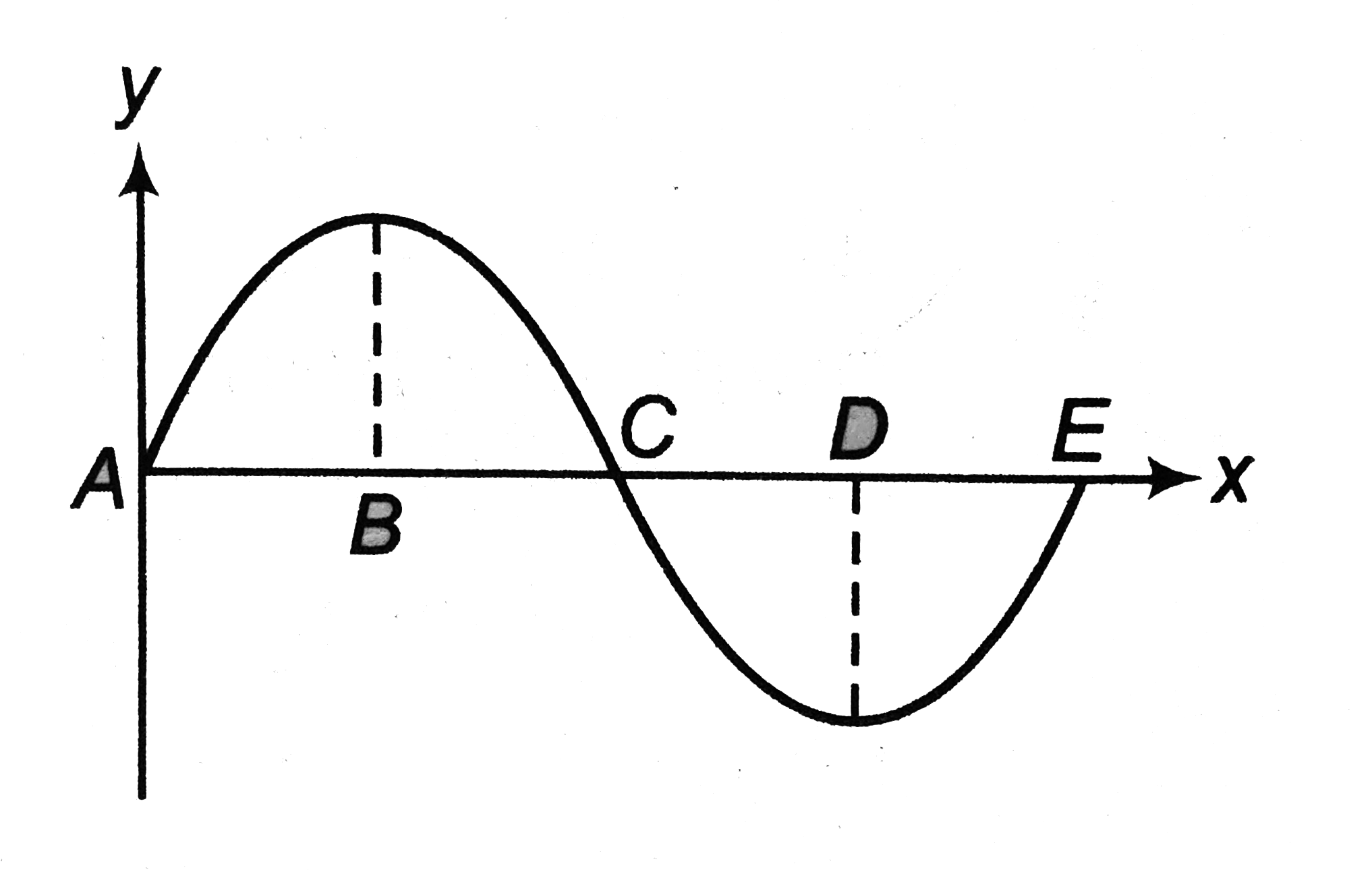
View SolutionSound waves are trqvelling along positive x - direction. Displacement of particle at any time t is as shows in figure. Select the correct statement.
View Solution
