The magnifications for two positions of image of the same lens are 3 and 2, of a fix point object on a fix screen when the distance between the two positions of lens is 30 cm .
The focal lengths of the lens is
180 cm
90 cm
30 cm
15 cm
The correct Answer is:A
To solve the problem, we need to find the focal length of the lens given the magnifications for two positions of the lens and the distance between these positions.
1. Identify the Given Values:
- Magnification for the first position of the lens, m1=3
- Magnification for the second position of the lens, m2=2
- Distance between the two positions of the lens, d=30cm
2. Use the Formula for Focal Length:
The formula to find the focal length f of the lens when the magnifications and distance between the lens positions are known is:
f=d⋅m1⋅m2m1−m2
3. Substitute the Values into the Formula:
Substitute d=30cm, m1=3, and m2=2 into the formula:
f=30⋅3⋅23−2
4. Calculate the Denominator:
Calculate m1−m2:
3−2=1
5. Calculate the Numerator:
Calculate 30⋅3⋅2:
30⋅3=90
90⋅2=180
6. Final Calculation of Focal Length:
Now, substitute back into the formula:
f=1801=180cm
7. Conclusion:
The focal length of the lens is 180cm.
Summary of the Solution:
The focal length of the lens is 180cm.
- Magnification for the first position of the lens, m1=3
- Magnification for the second position of the lens, m2=2
- Distance between the two positions of the lens, d=30cm
The formula to find the focal length f of the lens when the magnifications and distance between the lens positions are known is:
f=d⋅m1⋅m2m1−m2
Substitute d=30cm, m1=3, and m2=2 into the formula:
f=30⋅3⋅23−2
Calculate m1−m2:
3−2=1
Calculate 30⋅3⋅2:
30⋅3=90
90⋅2=180
Now, substitute back into the formula:
f=1801=180cm
The focal length of the lens is 180cm.
The focal length of the lens is 180cm.
Similar Questions
The distance between an object and a screen is 100 cm. A lens can produce real image of the object on the screen for two different position between the screen and the object. The distance between these two positions is 40 cm. If the power of the lens is close to (N100)D where N is integer, the value of N is ___________.
View SolutionIn the displacement method , a convex lens is placed in between an object and a screen . If one of them magnification is 3 and the displacement of the lens between the two positions is 24 cm , then the focal length of the lens is :-
View Solution
Knowledge Check
A concave lens forms the image of an object such that the distance between the object and image is 10cm and the magnification produced is 1/4. The focal length of the lens will be
A−6.2cmB−4.4cmC−8.6cmD−10cm
A convex lens is used to obtain a magnified image of an object on a screen . The object is at a distance 10 m from the lens . If the magnification is 19. the focal length of the lens is
View SolutionA cocave lens forms the image of an object such that the distance between the object and image is 10 cm and the magnification produced is 1/4. the focal length of the lens will be
View SolutionThe graph shown relationship between object distance and image distance for a equiconvex lens. Then focal length of the lens is
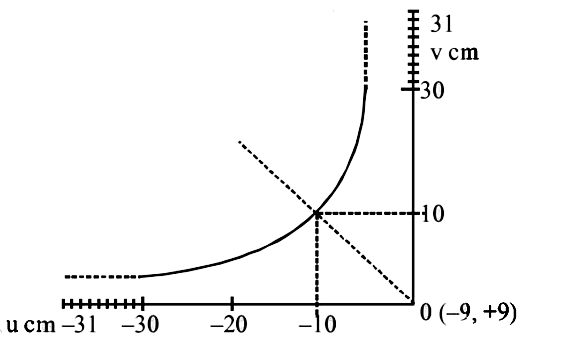
View SolutionFind the distance of an object from a convex lens if image is
two times magnified. Focal length of the lens is 10cm
View SolutionFind the distance of an object from a convex lens if image is
two times magnified. Focal length of the lens is 10cm
View SolutionAn object is placed 50cm from a screen as shown in figure.
A converging lens is moved such that line MN is its principal axis. Sharp images are formed on the screen in two positions of lens separated by 30cm. Find the focal length of the lens in cm.

View Solution(a) A screen is kept at a distance of 1m from the object. A converging lens between the object and the screen, when placed at any of the two positions which are 60cm apart, forms a sharp image of the object on the screen. Find the focal length of the lens.
(b) In the two positions of the lens, lateral size of the image is 4cm and 9cm. Find the size of the object.
View Solution
