A certain oscillation results from the addition of coherent oscillations of the same direction y=acos[ωt+(k−1)ϕ] where k is the number of oscillation [ k=1,2………N] and ϕ is the phase difference between kthand(K−1)th oscillations. The amplitude of resultant oscillation will be
asin(N/2)sin(ϕ/2)
asin(ϕ/2)
asin(nϕ)2
α
The correct Answer is:A
Step by step video & image solution for A certain oscillation results from the addition of coherent oscillations of the same direction y= a cos [omegat+(k-1)phi] where k is the number of oscillation [ k=1,2………N] and phi is the phase difference between k^("th") and (K-1)^("th") oscillations. The amplitude of resultant oscillation will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
For an LCR circuit, the power transferred from the driving source to the driven oscillator is P=I2Zcosϕ.
Athe power factor cosϕ≥0,P≥0Bthe driving force can give no energy to the oscillator(P = 0) in some cases.Cthe driving force cannot syphon out (P<0) the energy out of oscillator.Dall of these.
Which of the following curves represents correctly the oscillation given by y=y0sin(ωt−ϕ) where 0<ϕ<90∘?
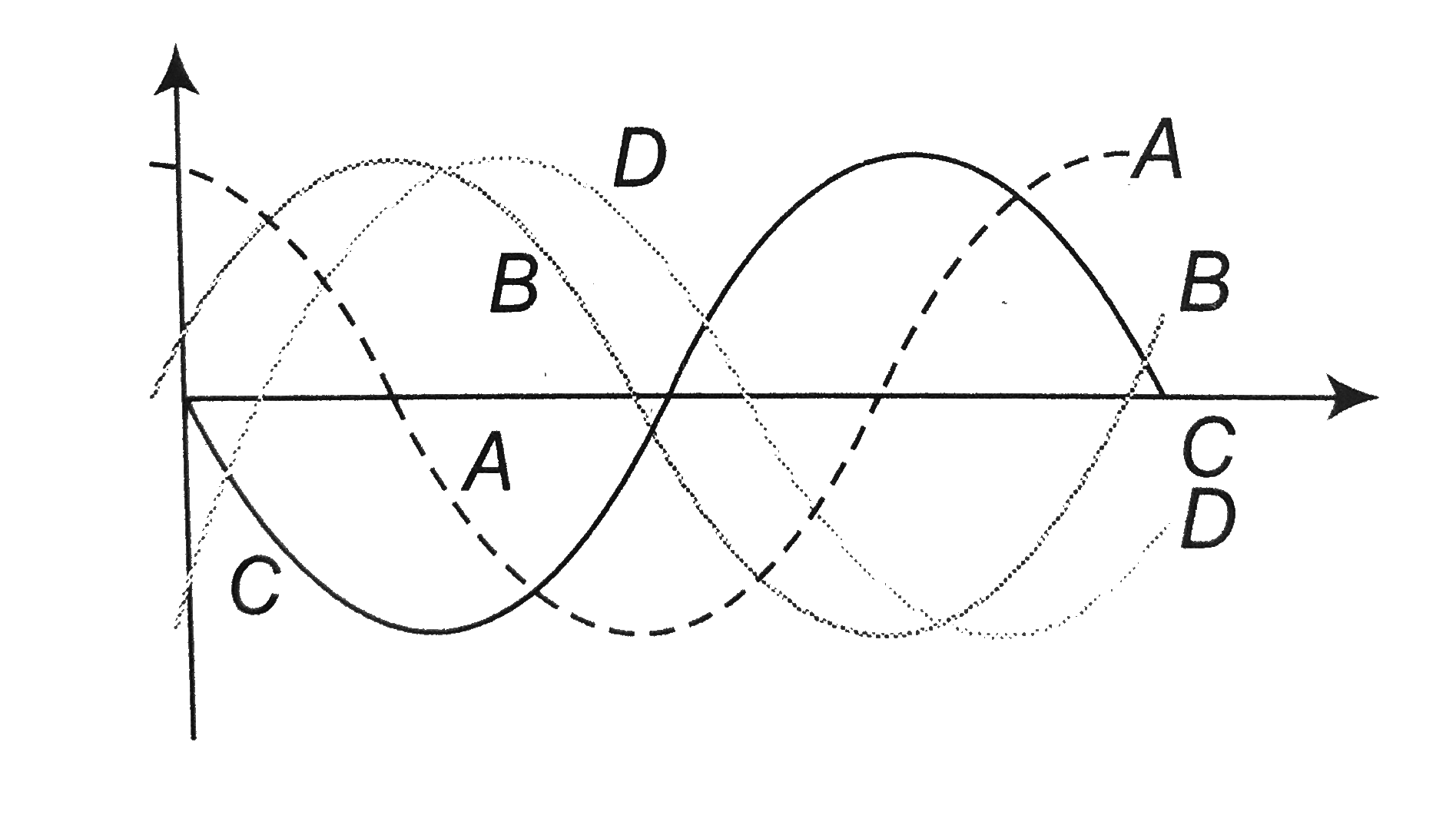 .
.
View SolutionOn the superposition of the two waves given as y1=A0sin(ωt−kx) and y2=A0cos(ωt−kx+π6) , the resultant amplitude of oscillations will be
View SolutionAn oscillation is superposition of three harmonic oscillations and decribed by the equation x=Asin2πυ1 where A changes with time according to A=A0(1+cos2πυ2t) with A0 to be constant. The frequencies of pure harmonic oscillations forming this oscillation are
View SolutionA spring of force constant 'k' is cut into four equal parts one part is attached with a mass m. The time period of oscillation will be
View SolutionA solid uniform cylinder of mass m performs small oscillations due to the action of two springs of stiffness k each (figure). Find the period of these oscillation in the absence of sliding.
x
View SolutionA sinusoidal wave travels along a taut string of linear mass density 0.1g/cm. The particles oscillate along y− direction and wave moves in the positive x− direction . The amplitude and frequency of oscillation are 2mm and 50Hz respectively. The minimum distance between two particles oscillating in the same phase is4m.
The tension in the string is ( in newton )
View SolutionAn object of mass 1kg executes simple harmonic oscillations along the x-axis, with a frequency of 2πHz. At the position x = 1 m, the object has a kinetic energy of 24 J. The amplitude of the oscillation is
View Solution
