A wave is travelling along x-axis . The disturbance at x=0 and t=0 is A/2 and is increasing , where A is amplitude of the wave. If , then the initial phase is . Find
The correct Answer is:
To solve the problem step by step, we will analyze the given wave function and the conditions provided.
Step 1: Write down the wave equation
The wave is described by the equation:
Y=sin(kx−ωt+ϕ)
Step 2: Substitute the initial conditions
We know that at x=0 and t=0, the disturbance Y is given as A2. Thus, we can write:
Y(0,0)=sin(0−0+ϕ)=sin(ϕ)
Setting this equal to A2, we have:
sin(ϕ)=A2
Step 3: Solve for ϕ
Since A is the amplitude of the wave, we can express the equation as:
sin(ϕ)=12
The solutions for ϕ that satisfy this equation are:
ϕ=π6+nπ
where n is any integer. However, we will consider the principal value first.
Step 4: Determine the increasing condition
The problem states that the disturbance is increasing at t=0 and x=0. This means that the derivative of Y with respect to t must be positive:
∂Y∂t=−ωcos(kx−ωt+ϕ)
At t=0 and x=0, this becomes:
∂Y∂t(0,0)=−ωcos(ϕ)
For the disturbance to be increasing, we need:
−ωcos(ϕ)>0
This implies:
cos(ϕ)<0
Step 5: Analyze the cosine condition
From the unit circle, we know that:
- cos(ϕ)<0 occurs in the intervals (π2,3π2).
Since we have ϕ=π6 from the sine condition, we need to check if this value satisfies the cosine condition.
Step 6: Find the correct value of ϕ
The value ϕ=π6 gives:
cos(π6)=√32>0
This does not satisfy the increasing condition. Therefore, we need to consider the next possible value:
ϕ=7π6
This value gives:
cos(7π6)<0
Thus, it satisfies the increasing condition.
Step 7: Relate ϕ to α
The problem states that the initial phase can be expressed as:
ϕ=απ
From our findings:
7π6=απ
Dividing both sides by π:
α=76
Final Answer
Thus, the value of α is:
α=76
The wave is described by the equation:
Y=sin(kx−ωt+ϕ)
We know that at x=0 and t=0, the disturbance Y is given as A2. Thus, we can write:
Y(0,0)=sin(0−0+ϕ)=sin(ϕ)
Setting this equal to A2, we have:
sin(ϕ)=A2
Since A is the amplitude of the wave, we can express the equation as:
sin(ϕ)=12
The solutions for ϕ that satisfy this equation are:
ϕ=π6+nπ
where n is any integer. However, we will consider the principal value first.
The problem states that the disturbance is increasing at t=0 and x=0. This means that the derivative of Y with respect to t must be positive:
∂Y∂t=−ωcos(kx−ωt+ϕ)
At t=0 and x=0, this becomes:
∂Y∂t(0,0)=−ωcos(ϕ)
For the disturbance to be increasing, we need:
−ωcos(ϕ)>0
This implies:
cos(ϕ)<0
From the unit circle, we know that:
- cos(ϕ)<0 occurs in the intervals (π2,3π2).
The value ϕ=π6 gives:
cos(π6)=√32>0
This does not satisfy the increasing condition. Therefore, we need to consider the next possible value:
ϕ=7π6
This value gives:
cos(7π6)<0
Thus, it satisfies the increasing condition.
The problem states that the initial phase can be expressed as:
ϕ=απ
From our findings:
7π6=απ
Dividing both sides by π:
α=76
Thus, the value of α is:
α=76
Similar Questions
A wave is travelling along X-axit. The disturbance at x=0 and t=0 is A/2 and is increasing. Where A is amplitute of the wave. If y=Asin(kx−ωt+∅), deetemine the initial phase empyset.
View SolutionA wave travelling along the x-axis is described by the equation y (x, t) = 0.005 sin (αx−βt). If the wavelength and time period of the wave are 0.08 m and 2 s respectively, then α,β in appropriate units are
View Solution
Knowledge Check
A wave travelling along the x-axis is described by the equation y (x, t) = 0.005 sin (αx−βt). If the wavelength and time period of the wave are 0.08 m and 2 s respectively, then α,β in appropriate units are
Aα=25π,β=πBα=0.08π,β=2πCα=0.04π,β=1πDα=12.5π,β=π2
A progressive wave travelling along the positive x-direction is represented by y(x,t)=Asin(kx−ωt+ϕ). Its snapshot at t=0 is given in the figure.
For this wave, the phase is:
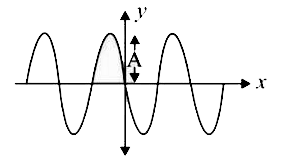
View SolutionA progressive wave travelling along the positive x-direction is represented by y(x,t)=Asin(kx−ωt+ϕ). Its snapshot at t=0 is given in the figure.
For this wave, the phase is:

View SolutionA wave is propagating in positive x−direction. A time t=0 its snapshot is taken as shown. If the wave equation is y=Asin(ωt−Kx+ϕ), then ϕ is
_2019_CBT7_E01_013_Q01.png)
View SolutionA wave is propagating in positive x−direction. A time t=0 its snapshot is taken as shown. If the wave equation is y=Asin(ωt−Kx+ϕ), then ϕ is
_2019_CBT7_E01_013_Q01.png)
View SolutionA wave is represente by y=Asin2(kx−ωt+ϕ). The amplitude and wavelength of wave is given by
View SolutionA wave travelling along the x-axis is described by the equation v(x,t)=0.005cos(αx−βt). If the wavelength and the time period of the wave are 0.08m and 2.0s, respectively, then αandβ in appropriate units are
View SolutionA wave travelling along the x-axis is described by the equation y(x,t)=0.005cos(αx−βt) . If the 1wavelength and the time period of the wave are 0.08m and 2.0s, respectively, then αβ=n×5, then the value of n is____(where α,β are in appropriate units).
View Solution
