A ball of mass m collides with a stationary identical ball a speed v0. Find the impulse of the colliding balls (e=1/2).
To solve the problem of finding the impulse of the colliding balls, we will follow these steps:
Step 1: Understand the situation
We have two identical balls, each of mass m. One ball is moving with an initial speed v0 and collides with a stationary ball. We need to find the impulse experienced by both balls during the collision.
Step 2: Apply the conservation of momentum
Since there are no external forces acting on the system, we can apply the principle of conservation of momentum. The total momentum before the collision must equal the total momentum after the collision.
Let:
- u1=v0 (initial velocity of the moving ball)
- u2=0 (initial velocity of the stationary ball)
- v1 = final velocity of the first ball after the collision
- v2 = final velocity of the second ball after the collision
The conservation of momentum can be expressed as:
mu1+mu2=mv1+mv2
Substituting the values:
mv0+0=mv1+mv2
This simplifies to:
v0=v1+v2(Equation 1)
Step 3: Use the coefficient of restitution
The coefficient of restitution e is given as 12. The coefficient of restitution is defined as:
e=v2−v1u1−u2
Substituting the known values:
12=v2−v1v0−0
This can be rearranged to:
v2−v1=v02(Equation 2)
Step 4: Solve the equations simultaneously
Now we have two equations:
1. v0=v1+v2
2. v2−v1=v02
From Equation 1, we can express v2 in terms of v1:
v2=v0−v1
Substituting this into Equation 2:
(v0−v1)−v1=v02
This simplifies to:
v0−2v1=v02
Rearranging gives:
2v1=v0−v02=v02
Thus:
v1=v04
Now substituting v1 back into Equation 1 to find v2:
v0=v04+v2
This leads to:
v2=v0−v04=3v04
Step 5: Calculate the impulse
Impulse is defined as the change in momentum. For the first ball:
Impulse=mv1−mu1=m(v04)−mv0=m(v04−v0)=m(−3v04)=−3mv04
For the second ball:
Impulse=mv2−mu2=m(3v04)−0=3mv04
The impulse experienced by the first ball is −3mv04 (indicating direction), while the second ball experiences 3mv04.
Final Answer
The magnitude of the impulse of the colliding balls is:
Impulse=3mv04
We have two identical balls, each of mass m. One ball is moving with an initial speed v0 and collides with a stationary ball. We need to find the impulse experienced by both balls during the collision.
Since there are no external forces acting on the system, we can apply the principle of conservation of momentum. The total momentum before the collision must equal the total momentum after the collision.
- u1=v0 (initial velocity of the moving ball)
- u2=0 (initial velocity of the stationary ball)
- v1 = final velocity of the first ball after the collision
- v2 = final velocity of the second ball after the collision
mu1+mu2=mv1+mv2
Substituting the values:
mv0+0=mv1+mv2
This simplifies to:
v0=v1+v2(Equation 1)
The coefficient of restitution e is given as 12. The coefficient of restitution is defined as:
e=v2−v1u1−u2
Substituting the known values:
12=v2−v1v0−0
This can be rearranged to:
v2−v1=v02(Equation 2)
Now we have two equations:
1. v0=v1+v2
2. v2−v1=v02
v2=v0−v1
Substituting this into Equation 2:
(v0−v1)−v1=v02
This simplifies to:
v0−2v1=v02
Rearranging gives:
2v1=v0−v02=v02
Thus:
v1=v04
Now substituting v1 back into Equation 1 to find v2:
v0=v04+v2
This leads to:
v2=v0−v04=3v04
Impulse is defined as the change in momentum. For the first ball:
Impulse=mv1−mu1=m(v04)−mv0=m(v04−v0)=m(−3v04)=−3mv04
For the second ball:
Impulse=mv2−mu2=m(3v04)−0=3mv04
The impulse experienced by the first ball is −3mv04 (indicating direction), while the second ball experiences 3mv04.
The magnitude of the impulse of the colliding balls is:
Impulse=3mv04
Similar Questions
A glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
View SolutionA ball of mass m collides with a stationary wedge of mass M, perpendicular to its inclined face, inclined at an angle as shown in the figure. If the coefficient of restitution between the wedge and ball is e, calculate the ratio of modulus of velocity of the ball immediately after and before collision. Also calculate the velocity of wedge just after collision.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eBe−1e+1C1+e1−eDe+1e−1 - Question 2 - Select One
A ball of mass m moving with a speed 2v0 collides head-on with an identical ball at rest. If e is the coefficient of restitution, then what will be the ratio of velocity of two balls after collision?
A1−e1+eB1+e1−eCe−1e+1De+1e−1 - Question 3 - Select One
A ball of mass m collides with a wall with speed v and rebounds on the same line with the same speed. If the mass of the wall is taken as infinite, then the work done by the ball on the wall is
Amv2B12mv2C2mvDzero
The ball A collides elastically with an identical ball B with a speed v. The ball B touches another identical ball C. The velocity of C, after the impact, is equal to
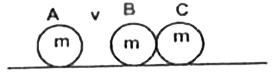 View Solution
View SolutionA ball of mass m collides with the ground at an angle. With the vertical. If the collision lasts for time t, the average force exerted by the ground on the ball is : (e = coefficient of restitution between the ball and the ground)
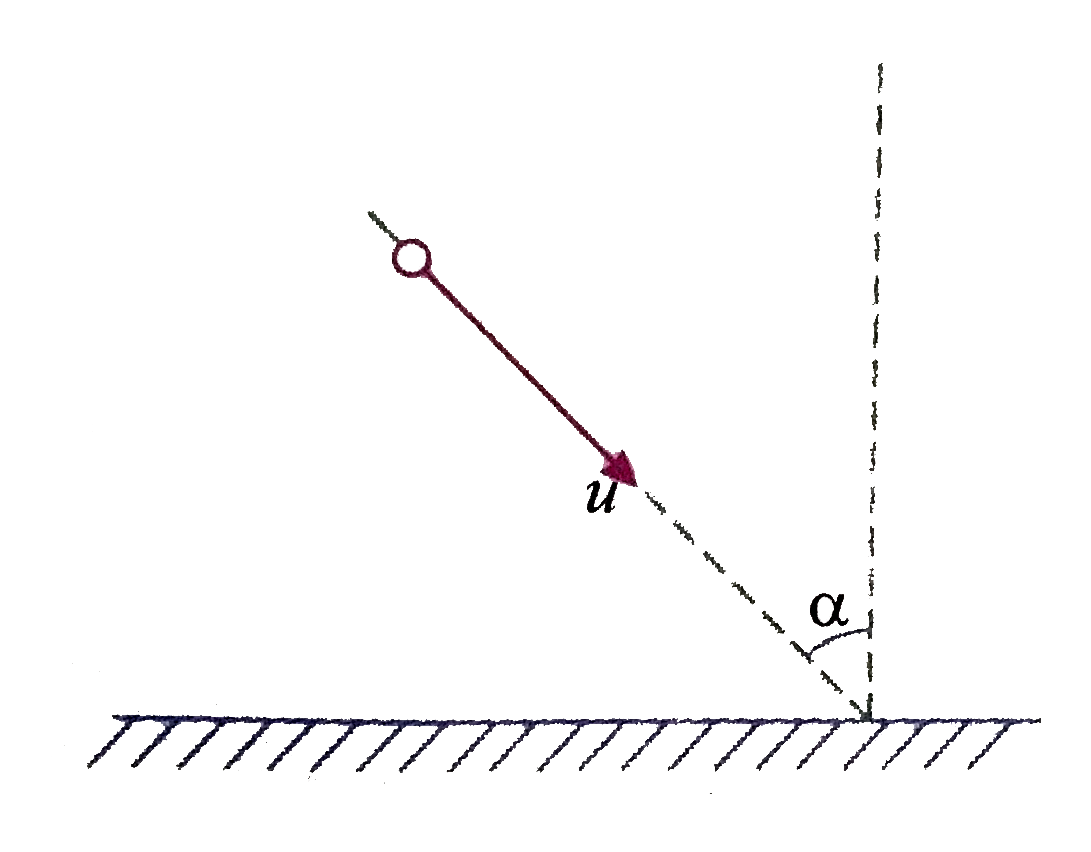 .View Solution
.View SolutionA stick of length L and mass M lies on a frictionless horizontal surface on which it is free to move in any way. A ball of mass m moving with speed v collides elastically with the stick as shown in the figure. If after the collision the ball comes to rest, then what would be the mass of the ball?
 View Solution
View SolutionA ball of mass m moving at a speed v makes a head-on collision with an identical ball at rest. The kinetic energy of the balls after the collision is three fourths of the original. Find the coefficient of restitution.
View SolutionA ball of mass m moving at a speed v makes a head on inelastic collision with an identical ball at rest. The kinetic energy of the balls after the collision is 34th of the original. Find the coefficient of restitution.

 View Solution
View Solution

