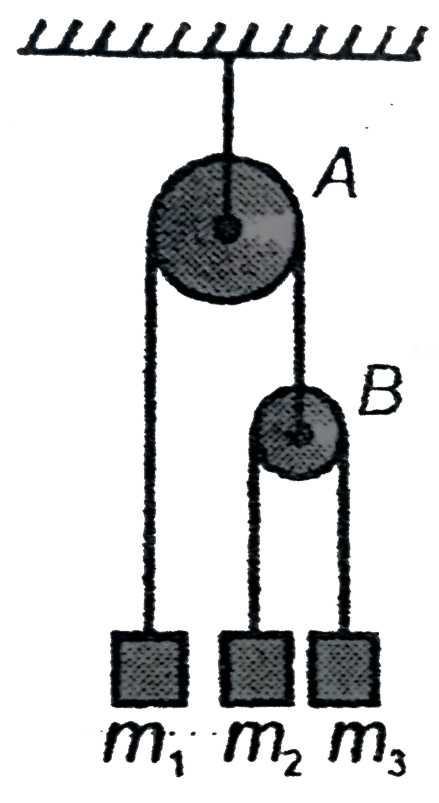
Find the relation between acceleration of the two blocks m1andm2. Assume pulleys are massless and frictionless and the strings are inextensible .
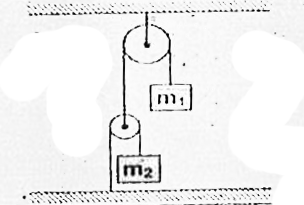
Step by step video & image solution for Find the relation between acceleration of the two blocks m_(1) and m_(2). Assume pulleys are massless and frictionless and the strings are inextensible . by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Find the accelerations of two blocks. Assume pulleys and strings are massless and frictionless. Also assume the string to be inextensible.
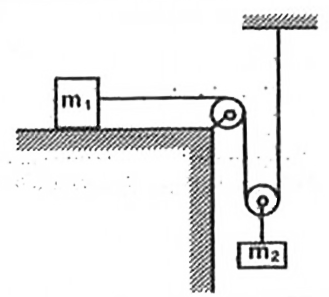
View SolutionIn the given diagram , find the relation between acceleration of blocks m1andm2 . (m2 remains horizontal ).
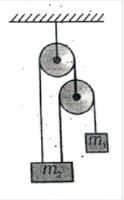
View SolutionFind the acceleration of blocks in fig. The pulley and the string are massless.

View SolutionIn the figure given below, with what acceleration does the block of mass m will move? (Pulley and strings are massless and frictionless)
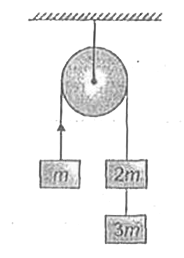
View SolutionIn the arrangement , shown below pulleys are massless and frictionless and threads are inextensible , block of mass m1 will remain at rest if
View SolutionIn the figure given below , with what acceleration does the block of mass m will move ? ( Pulley and strings are massless and frictionless)

View SolutionThe time period of block of mass m is (Assume pulleys and string are massless)
_PHY_E06_345_Q01.png) .
.
View SolutionIn an atwood machine the two blocks have massess 1kg and 3kg. The pulley is massless and frictionless and string is light. The acceleration of the centre of mass (in m/s2) of this system is 0.5x. Find the value of x.
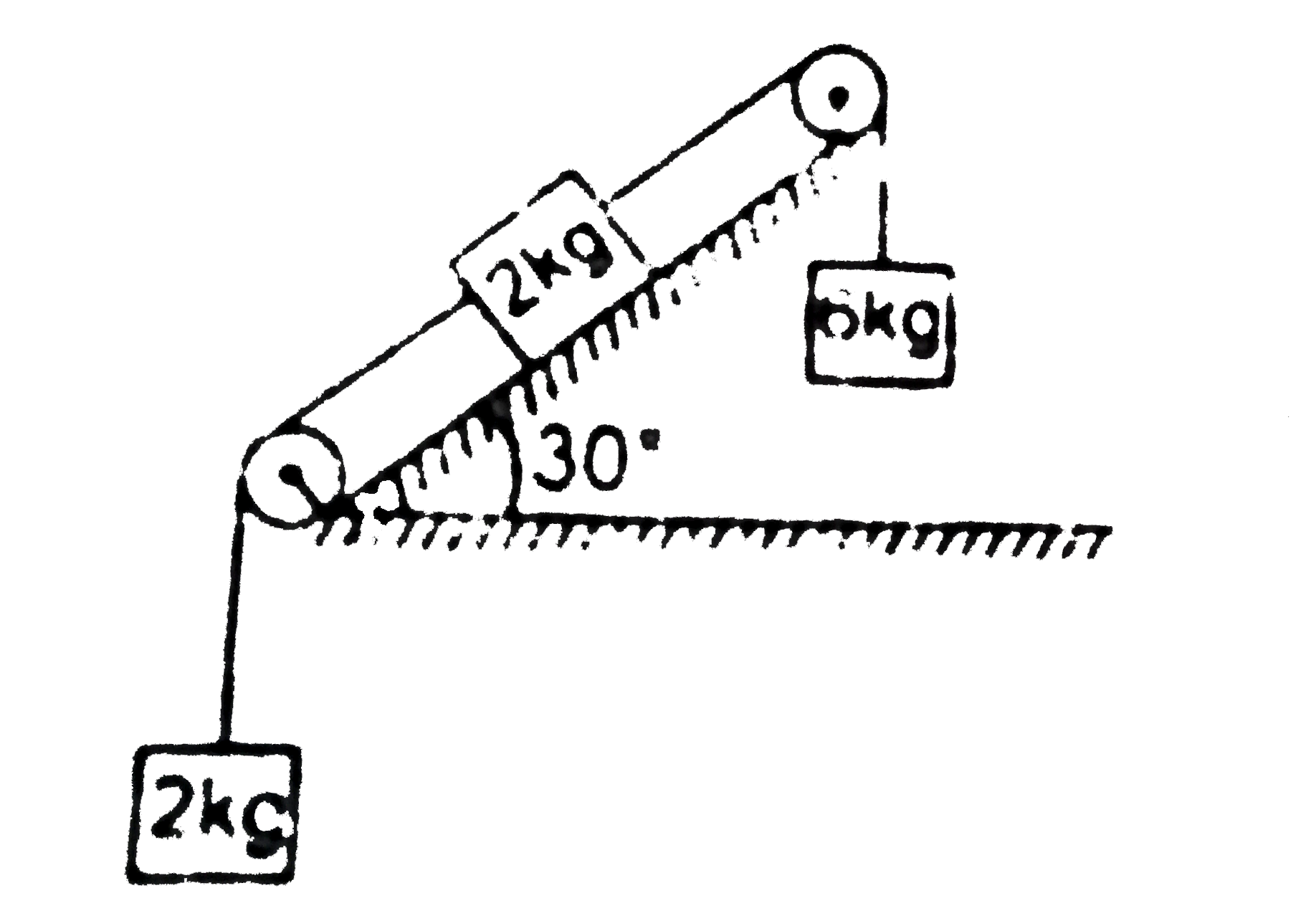
View SolutionFind the acceleration of the 6 kg block in the figure. All the surfaces and pulleys are smooth. Also the strings are inextensible and light. [Take g=10m/s2]
 .
.
View Solution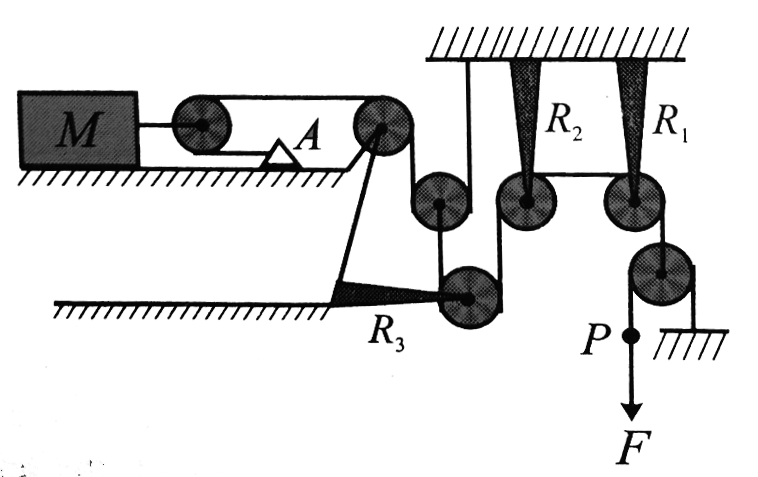
In the given arrangement, mass of the block is M and the surface on which the block is placed is smooth. Assuming all pulleys to be massless and frictionless, strings to be inelastic and light, R1,R2 and R3 to be light supporting rods, then acceleration of point P will be (A is fixed):
View Solution
