In an atwood machine the two blocks have massess 1kg and 3kg. The pulley is massless and frictionless and string is light. The acceleration of the centre of mass (in m/s2) of this system is 0.5x. Find the value of x.
To solve the problem of the Atwood machine with masses of 1 kg and 3 kg, we will follow these steps:
Step 1: Understand the Forces Acting on the Masses
In an Atwood machine, we have two masses connected by a string over a pulley. The forces acting on the masses are:
- For the 3 kg mass (m2): Weight (downward) = m2g=3×9.8=29.4N
- For the 1 kg mass (m1): Weight (downward) = m1g=1×9.8=9.8N
Step 2: Write the Equations of Motion
Using Newton's second law, we can write the equations for both masses.
- For the 3 kg mass (m2):
m2g−T=m2a(1)
Substituting m2=3kg:
29.4−T=3a
- For the 1 kg mass (m1):
T−m1g=m1a(2)
Substituting m1=1kg:
T−9.8=1a
Step 3: Solve the Equations Simultaneously
From equation (1):
T=29.4−3a(3)
Substituting equation (3) into equation (2):
(29.4−3a)−9.8=1a
Simplifying:
29.4−9.8−3a=1a
19.6=4a
a=19.64=4.9m/s2
Step 4: Calculate the Acceleration of the Center of Mass
The acceleration of the center of mass (a_cm) is given by:
acm=∑miai∑mi
Where:
- m1=1kg with a1=4.9m/s2 (upward)
- m2=3kg with a2=−4.9m/s2 (downward)
Calculating:
acm=(1×4.9)+(3×−4.9)1+3
=4.9−14.74=−9.84=−2.45m/s2
Step 5: Relate to Given Expression
The problem states that the acceleration of the center of mass is 0.5x:
−2.45=0.5x
Solving for x:
x=−2.450.5=−4.9
Step 6: Final Value of x
Since we are looking for the absolute value:
x=4.9
Conclusion
The value of x is 4.9.
In an Atwood machine, we have two masses connected by a string over a pulley. The forces acting on the masses are:
- For the 3 kg mass (m2): Weight (downward) = m2g=3×9.8=29.4N
- For the 1 kg mass (m1): Weight (downward) = m1g=1×9.8=9.8N
Using Newton's second law, we can write the equations for both masses.
- For the 3 kg mass (m2):
m2g−T=m2a(1)
Substituting m2=3kg:
29.4−T=3a
T−m1g=m1a(2)
Substituting m1=1kg:
T−9.8=1a
From equation (1):
T=29.4−3a(3)
Substituting equation (3) into equation (2):
(29.4−3a)−9.8=1a
Simplifying:
29.4−9.8−3a=1a
19.6=4a
a=19.64=4.9m/s2
The acceleration of the center of mass (a_cm) is given by:
acm=∑miai∑mi
Where:
- m1=1kg with a1=4.9m/s2 (upward)
- m2=3kg with a2=−4.9m/s2 (downward)
acm=(1×4.9)+(3×−4.9)1+3
=4.9−14.74=−9.84=−2.45m/s2
The problem states that the acceleration of the center of mass is 0.5x:
−2.45=0.5x
Solving for x:
x=−2.450.5=−4.9
Since we are looking for the absolute value:
x=4.9
The value of x is 4.9.
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - H) Multiple True-False Type Questions
4 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - I) Subjective Type Questions
8 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - F) Matrix-Match Type Questions
8 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
In the arrangement shown the fixed pulley is massless and frictionless. If the acceleration of block of mass 1kg is 30xm/s2. Find the value of x.
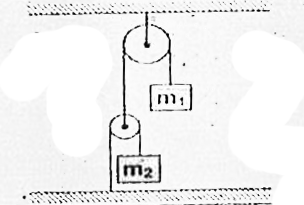
View SolutionFind the relation between acceleration of the two blocks m1andm2. Assume pulleys are massless and frictionless and the strings are inextensible .
View SolutionTwo masses 6 kg and 4 kg are connected by massless flexible and inextensible string passing over massless and frictionless pulley.The acceleration of centre of mass is (g=10ms^2)
View Solution
For the following system shown assume that pulley is frictionless, string is massless (m remains on M),
Q. The acceleration of the block A is
View Solution
For the following system shown assume that pulley is frictionless, string is massless (m remains on M),
Q. The acceleration of the block A is
View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
View SolutionIn the above example, if two blocks have masses 1kg and 2kg respectively then find their acceleration and tension in different string.
View SolutionFind the acceleration of two masses as shown in figure . The pulley are light and frictionless and string are light and frictionless and string are light and inextensible.

View SolutionFind the accelerations of two blocks. Assume pulleys and strings are massless and frictionless. Also assume the string to be inextensible.
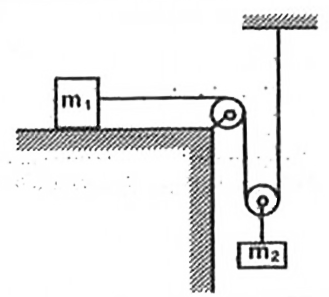
View Solution
