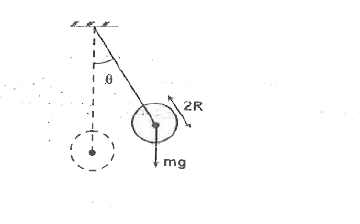
A spherical bob of mass m and radius R is attached to a fixed point by means of a massless rigid rod whose length from the point of support up to the centre of bob is l. Find the period of small oscillation.
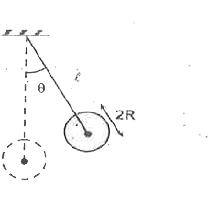
ld2θdt2=−mglsinθ≅−mglθ
where l=25mR2+ml2
=m(25R2+l2)
∴d2θdt2=−mglθm(25R2+l2)
⇒T=2π√5l2+2R25gl
Similar Questions
There is a rod of length l and mass m. It is hinged at one end to the ceiling. The period of small oscillation is
View SolutionFind the moment of inertia A of a spherical ball of mass m and radius r attached at the end of a straight rod of mass M and length l, if this system is free to rotate about an axis passing through the end of the rod (end of the rod opposite to sphere).
View Solution
Knowledge Check
- Question 1 - Select One
Two masses each of mass M are attached to the end of a rigid massless rod of length L. The moment of interia of the system about an axis passing centre of mass and perpendicular to its length is.
AML2/4BML2/2CML2D2ML2
A uniform rod of mass m and length l is suspended about its end. Time period of small angular oscillations is
View SolutionA point particle of mass M is attached to one end of a massless rigid non-conducting rod of length L. Another point particle of the same mass is attached to the other end of the rod. The two particles carry charges +q and −q respectively. This arrangement is held in a region of a uniform electric field E such that the rod makes a small angle θ (say of about 5 degree) with the field direction, fig. Find an expression for the minimum time needed for the rod to become parrallel to the field after it is set free.
View SolutionA uniform plank of mass m, free to move in the horizontal direction only , is placed at the top of a solid cylinder of mass 2m and radius R. The plank is attached to a fixed wall by mean of a light spring constant k. There is no slipping between the cylinder and the planck , and between the cylinder and the ground. Find the time period of small oscillation of the system.
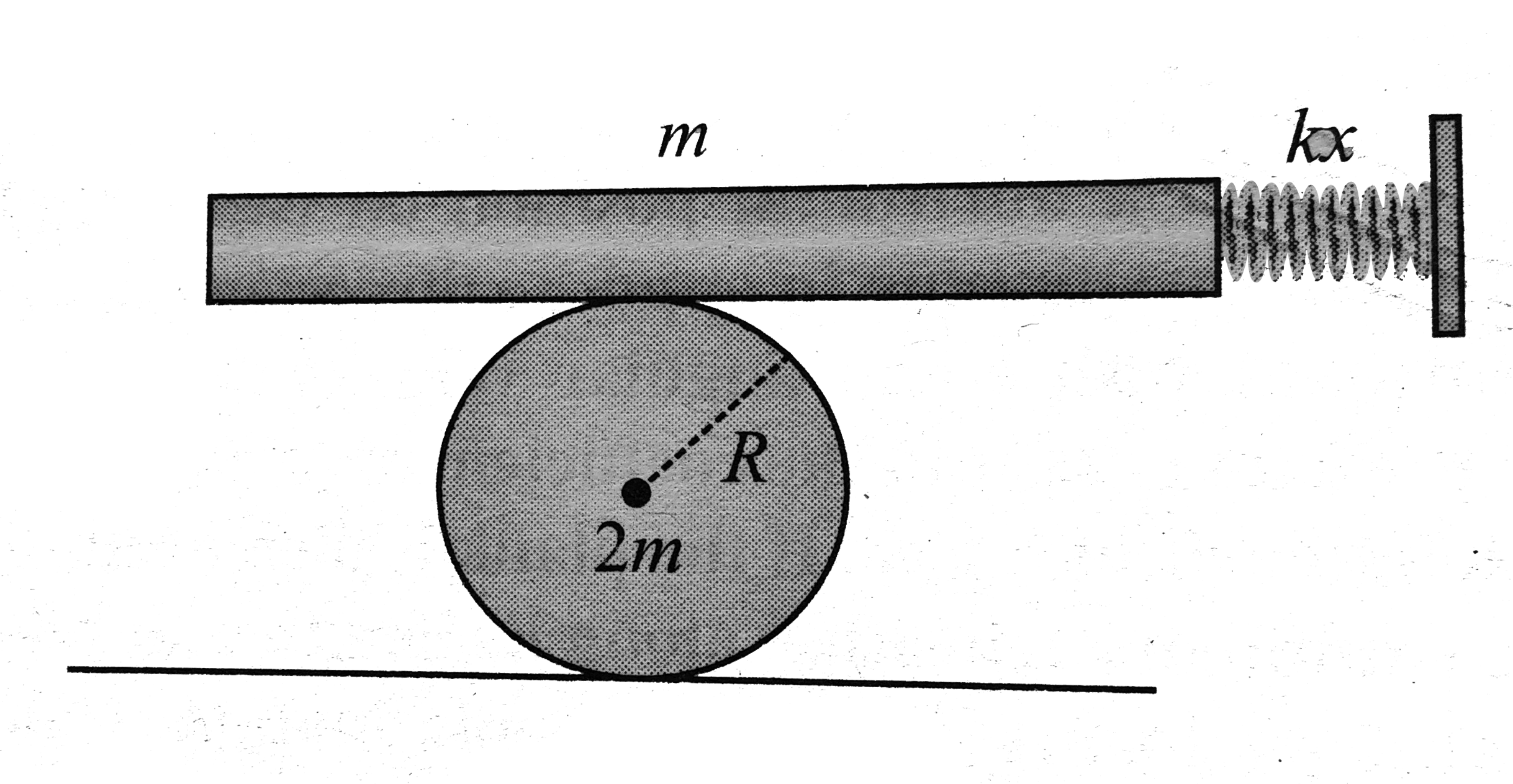View SolutionTwo spheres each of mass M and radius R/2 are connected with a massless rod of length R. Find the moment of inertia of the system about an axis passing through the centre of one of the sphere and perpendicular to the rod
View SolutionA spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
View SolutionA massless rod rigidly fixed at O. A sting carrying a mass m at one end is attached to point A on the rod so that OA=a. At another point B(OB=b) of the rod, a horizontal spring of force constant k is attached as shown. Find the period of small vertical oscillations of mass m around its euqilibrium position.
_E01_116_Q01.png)
View SolutionA rod of length L, cross sectional area A and density ρ is hanging from a rigid support by spring of stiffries k. A very small sphere of mass m is rigidly attached at the bottom of the rod. The rod is partially immersed in a liquid of density ρ. Find the period of small oscillations.
View Solution