The magnetic field at the origin due to a current element I (→dl)placedataposi→n(→r)is
((μ0i4π) →dl×→rr3⎞⎠
⎛⎝−⎛⎝(μ0)i4π⎛⎝→r×→dlr3⎞⎠⎞⎠⎞⎠
⎛⎝(μ0)i4π⎛⎝→r×→dlr3⎞⎠⎞⎠
⎛⎝−⎛⎝(μ0)i4π→dl×→rr3⎞⎠⎞⎠
The correct Answer is:C, D
To find the magnetic field at the origin due to a current element Id→l placed at a position →r, we can use the Biot-Savart law. Here’s a step-by-step solution:
Step 1: Understand the Biot-Savart Law
The Biot-Savart law states that the magnetic field →B at a point in space due to a current element is given by the formula:
→B=μ04πId→l×→r|→r|3
where:
- μ0 is the permeability of free space,
- I is the current,
- d→l is the current element vector,
- →r is the position vector from the current element to the point where the magnetic field is being calculated.
Step 2: Define the Position Vector
In this problem, we need to find the magnetic field at the origin (0,0) due to the current element located at position →r. The position vector from the current element to the origin is:
→rorigin=−→r
This means we need to consider the negative of the position vector →r when applying the Biot-Savart law.
Step 3: Substitute into the Biot-Savart Law
Substituting →rorigin into the Biot-Savart law, we have:
→Borigin=μ04πId→l×(−→r)|−→r|3
Since the magnitude of −→r is the same as →r, we can simplify this to:
→Borigin=−μ04πId→l×→r|→r|3
Step 4: Final Expression
Thus, the magnetic field at the origin due to the current element Id→l placed at position →r is given by:
→Borigin=−μ0I4πd→l×→r|→r|3
Summary
The magnetic field at the origin due to the current element can be expressed as:
→Borigin=−μ0I4πd→l×→r|→r|3
The Biot-Savart law states that the magnetic field →B at a point in space due to a current element is given by the formula:
→B=μ04πId→l×→r|→r|3
where:
- μ0 is the permeability of free space,
- I is the current,
- d→l is the current element vector,
- →r is the position vector from the current element to the point where the magnetic field is being calculated.
In this problem, we need to find the magnetic field at the origin (0,0) due to the current element located at position →r. The position vector from the current element to the origin is:
→rorigin=−→r
This means we need to consider the negative of the position vector →r when applying the Biot-Savart law.
Substituting →rorigin into the Biot-Savart law, we have:
→Borigin=μ04πId→l×(−→r)|−→r|3
Since the magnitude of −→r is the same as →r, we can simplify this to:
→Borigin=−μ04πId→l×→r|→r|3
Thus, the magnetic field at the origin due to the current element Id→l placed at position →r is given by:
→Borigin=−μ0I4πd→l×→r|→r|3
The magnetic field at the origin due to the current element can be expressed as:
→Borigin=−μ0I4πd→l×→r|→r|3
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - exercise
60 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 1
12 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer
6 Videos
Similar Questions
The magnetic field at the origin due to a current element I→dl placed at position r is
(i) (μ0i4π)(d→l×→rr3)
−(μ0i4π)(d→l×→rr3)
(iii) (μ0i4π)(→r×d→lr3)
−(μ0i4π)(→r×d→lr3)
View SolutionThe magnetic field at the origin due to the current flowing in the wire is

View SolutionThe magnetic field at the origin due to the current flowing in the wire is

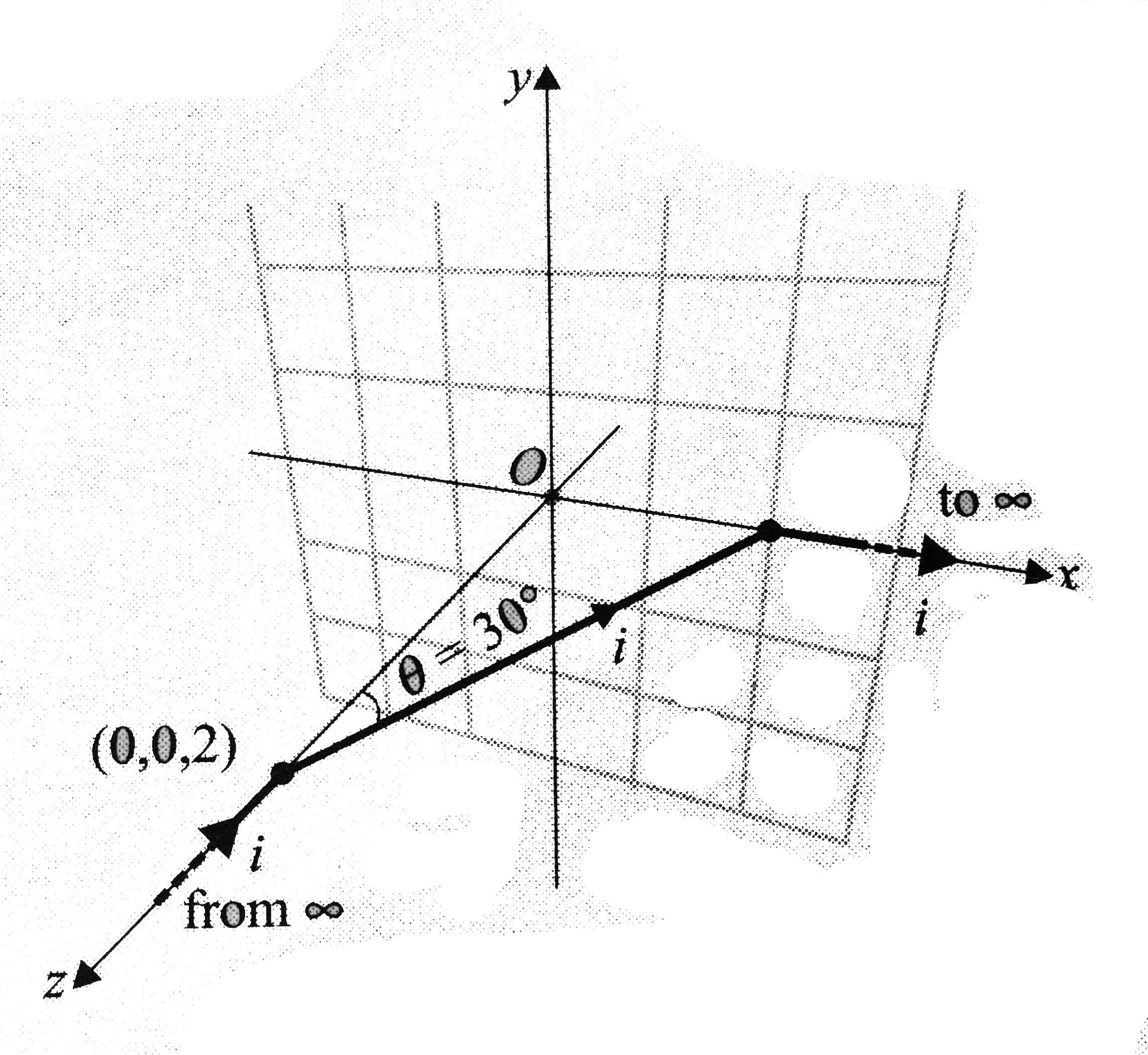
View SolutionFind the field at the origin O due to the current i=2A.
View SolutionThe magnetic field ¯¯¯¯¯dB due to a small current element ¯¯¯dl at a distance →r and carrying current 'I' is
View SolutionFind the magnetic field at the ccentre of a current carrying conductor bent in the form of an arc subtending angle θ at its centre. Radius of the arc is R
Strategy: Let the arc lie in x-y plane with its centre at the origin. Consider a small current element i→dl as shown. The field due to this element at the centre can be obtained by Biot-Savart law
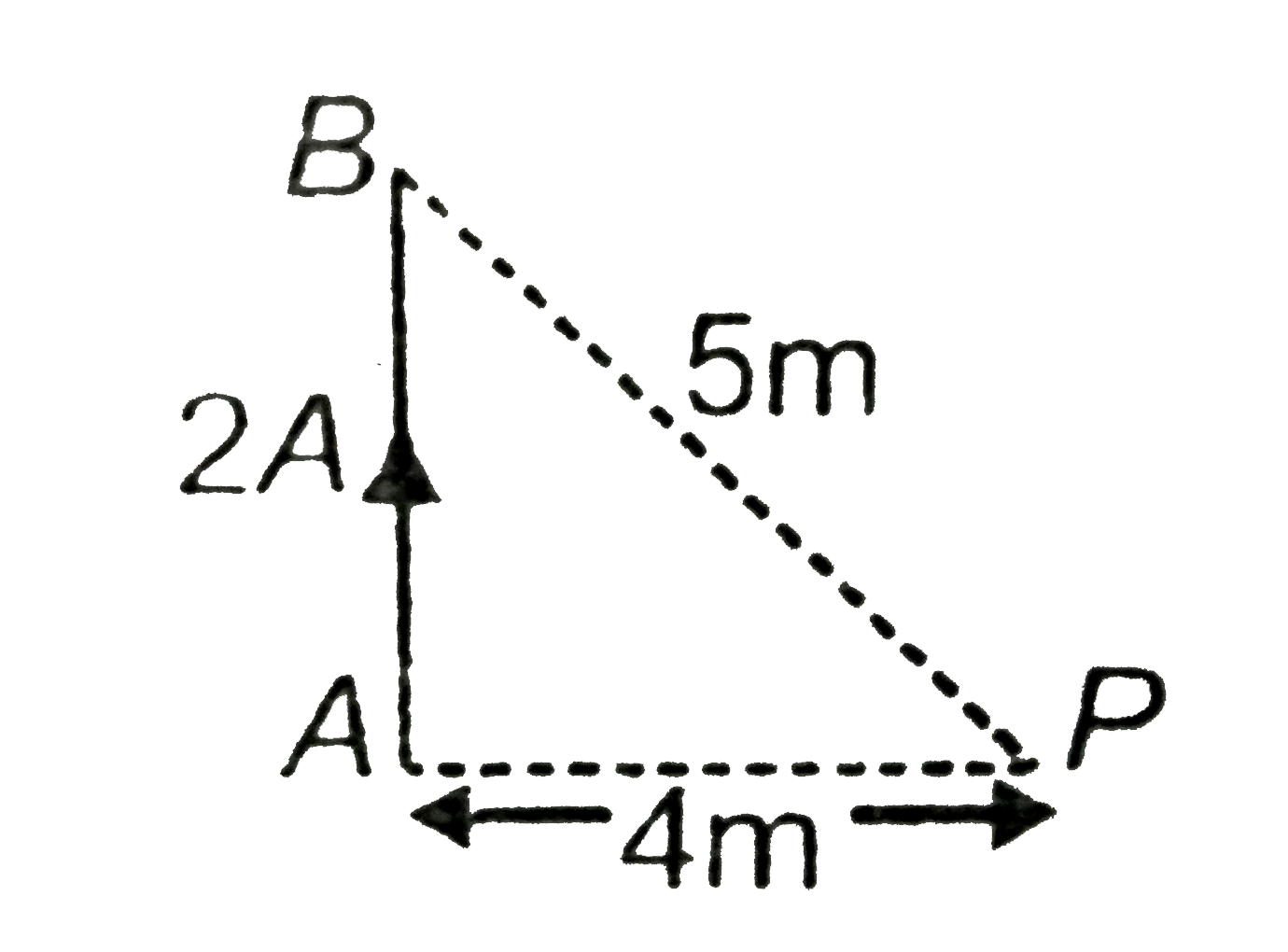
View SolutionWhat is the magnetic field ∣∣→B∣∣ at the point P due to a current carrying wire of length AB (having a current of 2A) shown in figure ?
View SolutionA: In any magnetic field region the line integral ∮→B.→dl along a closed loop is always zero.
R: The magnetic field →B in the expressioin ∮→B.→dl is due to the currents enclosed only by the loop.
View SolutionThe electric field intensity →E , , due to an electric dipole of dipole moment →p , at a point on the equatorial line is :
View SolutionAn external magnetic field is decreased to zero, due to which a current is induced in a circular wire loop of radius r and resistance R placed in the field. This current will not become zero at the instant when B stops changing
View Solution
