The magnitude of the earth's magnetic field at the north pole is B0 . A horizontal conductor of length l moves with a velocity v . The direction of v is perpendicular to the conductor. The induced emf is
(i) zero, if v is vertical
(ii) B0lv , if v is vertical
(iii) zero, if v is horizontal
(iv) B0lv , if v is horizontal
zero, if v is vertical
B0lv, if v is vertical
zero, if v is horizontal
B0 lv, if v is horizontal
The correct Answer is:A, D
To solve the problem, we will analyze the situation based on the given conditions and apply the principles of electromagnetic induction.
1. Understanding the Setup:
- We have a horizontal conductor of length l moving with a velocity v.
- The earth's magnetic field at the North Pole is denoted as B0.
- The direction of the velocity v is given as perpendicular to the conductor.
2. Case Analysis:
- We need to analyze two cases based on the direction of the velocity v: when v is vertical and when v is horizontal.
3. Case 1: v is Vertical:
- If v is vertical, it means that the velocity vector v is along the z-axis (let's assume ^k).
- The magnetic field B at the North Pole is directed downwards (along the negative z-axis).
- Since the direction of v is vertical and the conductor is horizontal, we can conclude that the velocity vector and the magnetic field vector are parallel.
- The induced EMF E can be calculated using the formula:
E=l⋅(v×B)
- Since v is parallel to B, the cross product v×B will be zero.
- Thus, the induced EMF is:
E=0
4. Case 2: v is Horizontal:
- If v is horizontal, we can assume v is along the x-axis (let's say ^i).
- The magnetic field B is still directed downwards (along the negative z-axis).
- The conductor is horizontal, and we can assume it is along the y-axis (let's say ^j).
- Now, we can calculate the induced EMF using the same formula:
E=l⋅(v×B)
- Here, v is along ^i and B is along −^k.
- The cross product v×B can be calculated:
^i×(−^k)=^j
- Therefore, the induced EMF becomes:
E=l⋅(v⋅^j)=l⋅v
- Since the magnitude of the magnetic field is B0, we can express the induced EMF as:
E=B0⋅l⋅v
5. Conclusion:
- From the analysis, we conclude:
- The induced EMF is zero if v is vertical.
- The induced EMF is B0lv if v is horizontal.
Final Answer:
- (i) Zero, if v is vertical.
- (iv) B0lv, if v is horizontal.
- We have a horizontal conductor of length l moving with a velocity v.
- The earth's magnetic field at the North Pole is denoted as B0.
- The direction of the velocity v is given as perpendicular to the conductor.
- We need to analyze two cases based on the direction of the velocity v: when v is vertical and when v is horizontal.
- If v is vertical, it means that the velocity vector v is along the z-axis (let's assume ^k).
- The magnetic field B at the North Pole is directed downwards (along the negative z-axis).
- Since the direction of v is vertical and the conductor is horizontal, we can conclude that the velocity vector and the magnetic field vector are parallel.
- The induced EMF E can be calculated using the formula:
E=l⋅(v×B)
- Since v is parallel to B, the cross product v×B will be zero.
- Thus, the induced EMF is:
E=0
- If v is horizontal, we can assume v is along the x-axis (let's say ^i).
- The magnetic field B is still directed downwards (along the negative z-axis).
- The conductor is horizontal, and we can assume it is along the y-axis (let's say ^j).
- Now, we can calculate the induced EMF using the same formula:
E=l⋅(v×B)
- Here, v is along ^i and B is along −^k.
- The cross product v×B can be calculated:
^i×(−^k)=^j
- Therefore, the induced EMF becomes:
E=l⋅(v⋅^j)=l⋅v
- Since the magnitude of the magnetic field is B0, we can express the induced EMF as:
E=B0⋅l⋅v
- From the analysis, we conclude:
- The induced EMF is zero if v is vertical.
- The induced EMF is B0lv if v is horizontal.
- (i) Zero, if v is vertical.
- (iv) B0lv, if v is horizontal.
Similar Questions
The magnitude of the earth's magnetic field at a place is B0 and angle of dip is δ. A horizontal conductor of lenth/lying along the magnetic north-south moves eastwards with a velocity v. The emf induced acroos the coductor is
View SolutionA glass rod of length l moves with velocity v in a uniform magnetic field B. What is the e.m.f induced in the rod?
View Solution
Knowledge Check
A conductor is moving with the velocity v in the magnetic field and induced current is I. If the velocity of conductor becomes double, the induced current will be
A0.5 IB1.5 IC2 ID2.5 I
A small conducting rod of length l, moves with a uniform velocity v in a uniform magnetic field B as shown in fig __

View SolutionA wire of length 50 cm moves with a velocity of 300 m/min, perpendicular to a magnetic field. If the emf induced in the wire is 2 V, then the magnitude of the field in tesla is
View SolutionA vertical conducting ring ogradius R falls vertically in a horizontal magnetic field of magnitude B. The direction of B is perpendicular to the plane of the ring. When the speed of the ring is v,

View SolutionA rod of length l is moving velocity v "in magnetic field" b as seen in . Find the emf induced in all three cases.
(a)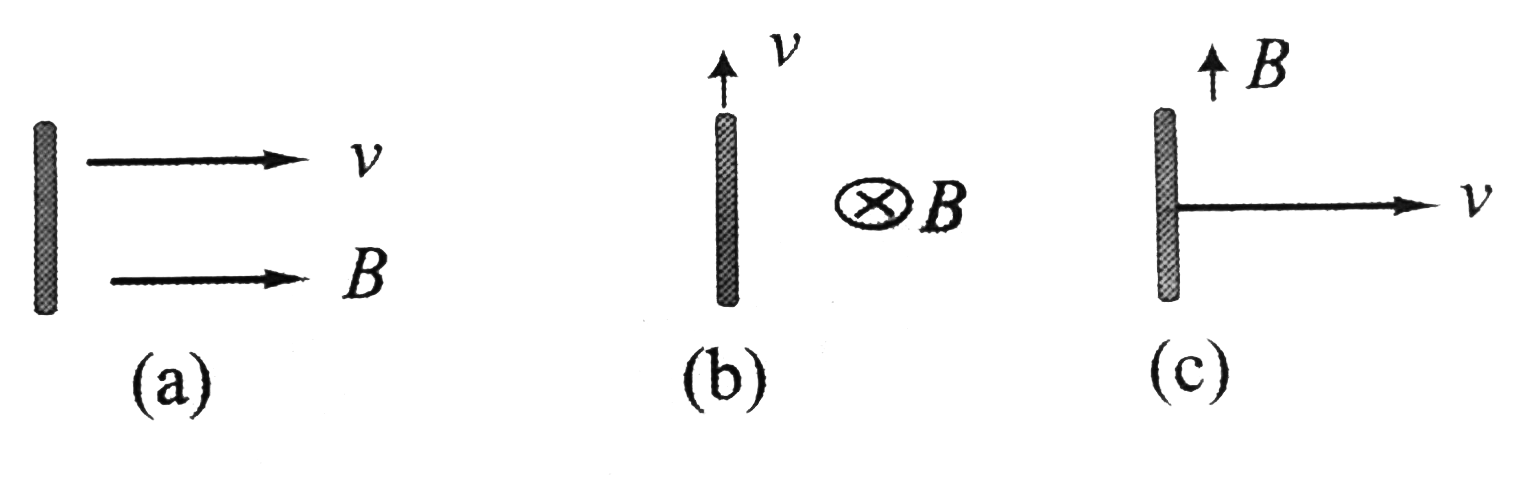
View SolutionA vertical rod of length l is moved with constant velocity v towards east. The vertical component of earth magnetic field is B and angle of dip is θ. The induced e.m.f. in the rod is
View SolutionA conducing rod of length l is falling with a velocity v perpendicular to a unifrorm horizontal magnetic field B . The potential difference between its two ends will be
View SolutionA metallic rod of length l is moved perpendicular to its length with velocity v in a magnetic field →B acting perpendicular to the plane in which rod moves. Derive the expression for the inducced emf.
View Solution