A flexible current loop is lying in a region where magnetic field is switchted on perpendicular to the loop and pointing up. What will be the direction of the induced current ?
To determine the direction of the induced current in a flexible current loop when a magnetic field is switched on perpendicular to the loop and pointing upwards, we can follow these steps:
1. Understand the Setup:
- We have a flexible current loop lying in a magnetic field that is initially off. When the magnetic field is switched on, it points upwards (perpendicular to the plane of the loop).
2. Identify the Change in Magnetic Flux:
- When the magnetic field is switched on, the magnetic flux through the loop changes. The magnetic flux (Φ) is given by the formula:
Φ=B⋅A⋅cos(θ)
where B is the magnetic field strength, A is the area of the loop, and θ is the angle between the magnetic field and the normal to the loop. Here, θ=0∘ since the field is perpendicular to the loop, leading to maximum flux.
3. Apply Faraday's Law of Electromagnetic Induction:
- According to Faraday's law, the induced electromotive force (emf) in the loop is given by:
emf=−dΦdt
- Since the magnetic field is increasing from zero to a certain value, the change in flux (dΦ) is positive, and thus the induced emf will be negative, indicating the direction of the induced current.
4. Use Lenz's Law:
- Lenz's Law states that the direction of the induced current will be such that it opposes the change in magnetic flux that produced it. Since the magnetic field is increasing upwards, the induced current will flow in a direction that creates a magnetic field opposing this increase.
5. Determine the Direction of Induced Current:
- To oppose the upward magnetic field, the induced current must create a magnetic field pointing downwards. According to the right-hand rule, if the induced current flows in a clockwise direction when viewed from above, it will create a downward magnetic field.
- Therefore, the induced current in the loop will be in the clockwise direction.
Final Answer:
The direction of the induced current will be clockwise.
---
- We have a flexible current loop lying in a magnetic field that is initially off. When the magnetic field is switched on, it points upwards (perpendicular to the plane of the loop).
- When the magnetic field is switched on, the magnetic flux through the loop changes. The magnetic flux (Φ) is given by the formula:
Φ=B⋅A⋅cos(θ)
where B is the magnetic field strength, A is the area of the loop, and θ is the angle between the magnetic field and the normal to the loop. Here, θ=0∘ since the field is perpendicular to the loop, leading to maximum flux.
- According to Faraday's law, the induced electromotive force (emf) in the loop is given by:
emf=−dΦdt
- Since the magnetic field is increasing from zero to a certain value, the change in flux (dΦ) is positive, and thus the induced emf will be negative, indicating the direction of the induced current.
- Lenz's Law states that the direction of the induced current will be such that it opposes the change in magnetic flux that produced it. Since the magnetic field is increasing upwards, the induced current will flow in a direction that creates a magnetic field opposing this increase.
- To oppose the upward magnetic field, the induced current must create a magnetic field pointing downwards. According to the right-hand rule, if the induced current flows in a clockwise direction when viewed from above, it will create a downward magnetic field.
- Therefore, the induced current in the loop will be in the clockwise direction.
The direction of the induced current will be clockwise.
Similar Questions
A current loop in a magnetic field
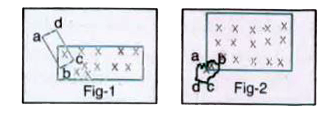
View SolutionFigures 1 and 2 show planar loops of different shapes moving out or into a region of magnetic field, which is directed normal to the plane of the loop and away for reader. Determine the direction of induced current
View SolutionA circular loop of wire is carring a current i (as shown in the figure). On applying a uniform magnetic field inward perpendicular to the plane of the loop, the loop

View SolutionA current loop placed in a magnetic field behaves like a
View SolutionA current carrying loop in a uniform magnetic field will experience
View SolutionFigure shows planar loops of different shapes moving out of or into a region of a magnetic field which is directed normal to the plane of the loop away from the reader. Determine the direction of induced current in each loop using Lenz's law.

View SolutionA loop of irregular shape of conducting wire PORS (as shown in figure) placed in a uniform magnetic field perpendicular to the plane of the paper changes into a circular shape. The direction of induced current will be
View SolutionTorque acting on a current loop in a uniform magnetic field is equal to
View SolutionA circular loop of radius R is kept in a uniform magnetic field pointing perpendicular into the plane of paper. When a current l flows in the loop, the tension produced in the loop is

View SolutionA square loop of side a carris a current I. The magnetic field at the centre of the loop is
View Solution
