If the minimum and maximum distance to revolve around the sun is x1 and x2 respectively. Calculate velocity to revolve is v0 then the maximum velocity is
v0(x1)2(x2)2
v0(x2)2(x1)2
v0x2x1
v0x1x2
To solve the problem, we will use the concept of conservation of angular momentum. The angular momentum of a planet revolving around the sun remains constant if no external torque acts on it.
1. Understanding the Problem:
We are given:
- Minimum distance from the Sun (perihelion) = x1
- Maximum distance from the Sun (aphelion) = x2
- Velocity at a distance x2 = v0
We need to find the maximum velocity v1 when the planet is at distance x1.
2. Applying Conservation of Angular Momentum:
The angular momentum L of the planet at distance x1 and x2 can be expressed as:
L=m⋅v1⋅x1=m⋅v0⋅x2
Here, m is the mass of the planet, v1 is the velocity at distance x1, and v0 is the velocity at distance x2.
3. Setting Up the Equation:
Since the mass m is common on both sides, we can cancel it out:
v1⋅x1=v0⋅x2
4. Solving for Maximum Velocity v1:
Rearranging the equation to solve for v1:
v1=v0⋅x2x1
5. Conclusion:
The maximum velocity v1 of the planet when it is at the minimum distance x1 from the Sun is given by:
v1=v0⋅x2x1
We are given:
- Minimum distance from the Sun (perihelion) = x1
- Maximum distance from the Sun (aphelion) = x2
- Velocity at a distance x2 = v0
We need to find the maximum velocity v1 when the planet is at distance x1.
The angular momentum L of the planet at distance x1 and x2 can be expressed as:
L=m⋅v1⋅x1=m⋅v0⋅x2
Here, m is the mass of the planet, v1 is the velocity at distance x1, and v0 is the velocity at distance x2.
Since the mass m is common on both sides, we can cancel it out:
v1⋅x1=v0⋅x2
Rearranging the equation to solve for v1:
v1=v0⋅x2x1
The maximum velocity v1 of the planet when it is at the minimum distance x1 from the Sun is given by:
v1=v0⋅x2x1
Topper's Solved these Questions
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:SECTION-A
Explore 80 Videos
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:SECTION-B
Explore 40 Videos
- JEE MAINBook:JEE MAINS PREVIOUS YEARChapter:JEE MAINExercise:All Questions
Explore 473 Videos
- JEE MAIN 2022Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2022Exercise:Question
Explore 492 Videos
Similar Questions
Knowledge Check
The planet which takes the maximum time to revolve around the sun is
AmarsBplutoCneptuneDuranusThe minimum and maximum distances of a planet revolving around sun are r and R . If the minimum speed of planet of its trajectory is v0 , its maximum speed will be
Av0RrBv0rRCv0R2r2Dv0r2R2Two satellites revolve around the ‘Sun’ as shown in the figure. First satellite revolves in a circular orbit of radius R with speed v1 . Second satellite revolves in elliptical orbit, for which minimum and maximum distance from the sun are R3 and 5R3 respectively. Velocities at these positions are v2 and v3 respectively. The correct order of speeds is
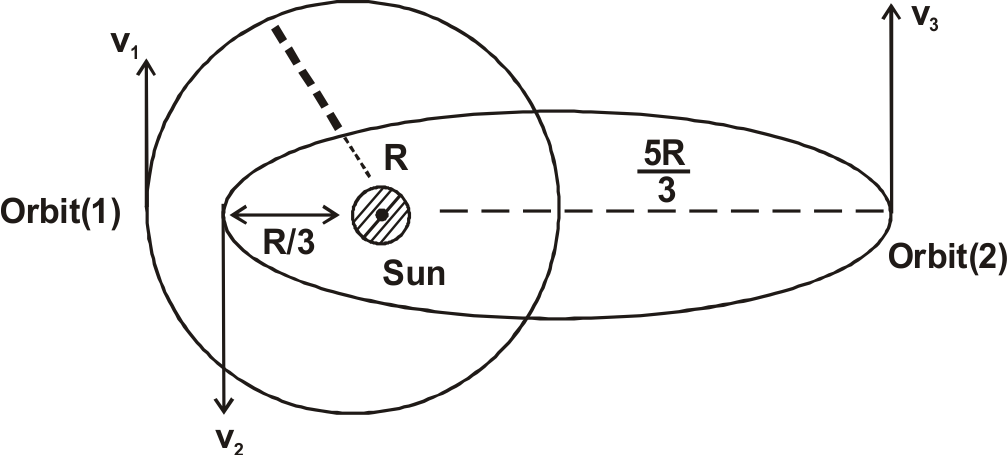 Av2>v3>v1Bv3<v2<v1Cv2>v1>v3Dv2>v3=v1
Av2>v3>v1Bv3<v2<v1Cv2>v1>v3Dv2>v3=v1
A point charge –q revolves around a fixed charge +Q in elliptical orbit. The minimum ar.d maximum distance of q from Q are r1 and r2, respectively. The mass of revolving particle is Q>q and assume no gravitational effects. Find the velocity of q at positions when it is at r1 and r2 distance from Q.
View SolutionThe maximum and minimum distances of a comet from the sun are 8×1012m and 1.6×1012m, respectively. If its velocity whien it is nearest to the sun is 60 m / s, then what will be its velocity (in m / s ). when it is farthest from the sun?
View SolutionA planet of mass m is revolving around the sun in an elliptical orbit. The minimum and maximum distances of the planet from the sun are s1 and s2. Derive the relation between time period of the planet in terms of s1 and s2.
View SolutionThe areal velocity of the planets revolving around the sun is ………….. .
View SolutionFind the maximum and minimum distances of the planet A from the sun S, if at a ceration moment of times it was at a distance r0 and travelling with the velocity υ0. With the angle between the radius vector and velocity vector being equal to ϕ.
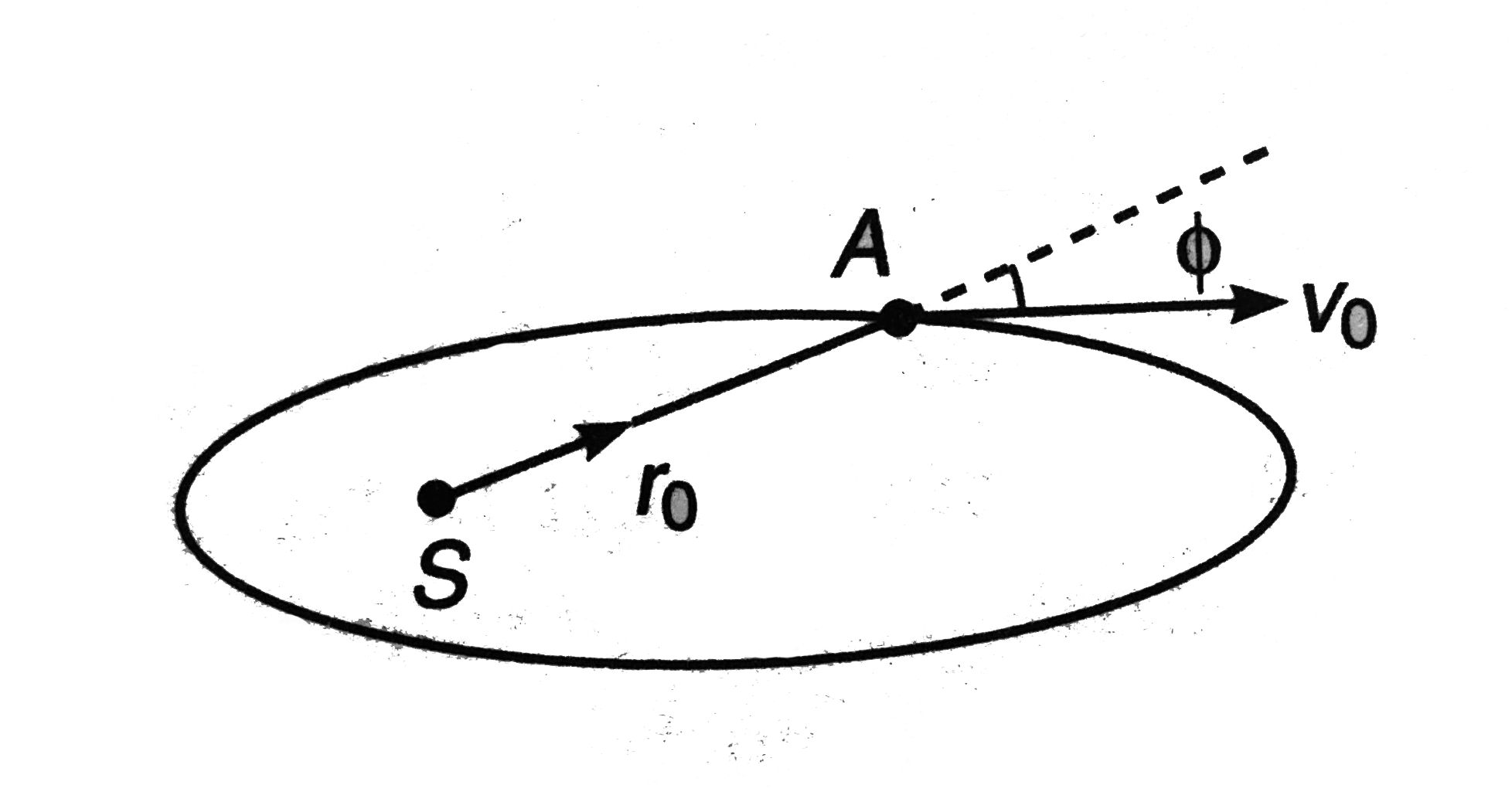
View Solution