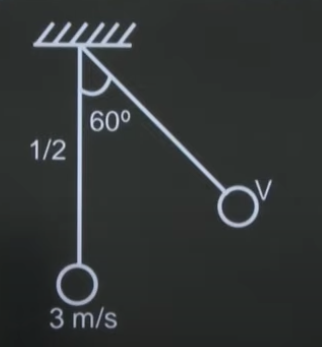
A particle tied to string of length 0.5m is given a velocity 3 m/s at its bottom point while undergoing vertical circular motion. What will be its speed when it makes an angle of 600 with lower vertical
1.5 m/s
2.5 m/s
2√2
2 m/s
To solve the problem, we will use the principle of conservation of mechanical energy. The total mechanical energy (kinetic energy + potential energy) at the bottom point (point A) will be equal to the total mechanical energy at the point where the particle makes an angle of 60∘ with the vertical (point B).
1. Identify the Given Values:
- Length of the string (radius of the circular motion), r=0.5m
- Initial velocity at the bottom point (point A), v1=3m/s
- Angle with the vertical at point B, θ=60∘
2. Calculate the Height (h) at Point B:
- The height gained when the particle moves from point A to point B can be calculated using the formula:
h=r−rcos(60∘)
- Since cos(60∘)=12:
h=r−r⋅12=r(1−12)=r⋅12=0.5⋅12=0.25m
3. Apply Conservation of Energy:
- At point A (bottom point):
- Kinetic Energy (KE) = 12mv21=12m(3)2=92m
- Potential Energy (PE) = 0 (taking this point as the reference level)
- At point B (when the particle is at an angle of 60∘):
- Kinetic Energy (KE) = 12mv22 (where v2 is the speed we want to find)
- Potential Energy (PE) = mgh=mg(0.25)
4. Set Up the Energy Conservation Equation:
Total Energy at A=Total Energy at B
92m=12mv22+mg(0.25)
5. Cancel the Mass (m) from the Equation:
92=12v22+g(0.25)
6. Substitute g (using g=10m/s2):
92=12v22+10⋅0.25
92=12v22+2.5
7. Rearrange to Solve for v22:
92−2.5=12v22
92−52=12v22
42=12v22
2=12v22
v22=4
8. Calculate v2:
v2=√4=2m/s
Final Answer:
The speed of the particle when it makes an angle of 60∘ with the lower vertical is 2m/s.
---
- Length of the string (radius of the circular motion), r=0.5m
- Initial velocity at the bottom point (point A), v1=3m/s
- Angle with the vertical at point B, θ=60∘
- The height gained when the particle moves from point A to point B can be calculated using the formula:
h=r−rcos(60∘)
- Since cos(60∘)=12:
h=r−r⋅12=r(1−12)=r⋅12=0.5⋅12=0.25m
- At point A (bottom point):
- Kinetic Energy (KE) = 12mv21=12m(3)2=92m
- Potential Energy (PE) = 0 (taking this point as the reference level)
- At point B (when the particle is at an angle of 60∘):
- Kinetic Energy (KE) = 12mv22 (where v2 is the speed we want to find)
- Potential Energy (PE) = mgh=mg(0.25)
Total Energy at A=Total Energy at B
92m=12mv22+mg(0.25)
92=12v22+g(0.25)
92=12v22+10⋅0.25
92=12v22+2.5
92−2.5=12v22
92−52=12v22
42=12v22
2=12v22
v22=4
v2=√4=2m/s
The speed of the particle when it makes an angle of 60∘ with the lower vertical is 2m/s.
Topper's Solved these Questions
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-A
80 Videos
- JEE MAIN 2021BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - SECTION-B
40 Videos
- JEE MAINBOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - All Questions
473 Videos
- JEE MAIN 2022BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question
492 Videos
Similar Questions
A simple pendulum of length 1/2m has initial speed 3m/s when pendulum mass is at lowermost point. What will be the speed pf pendulum mass, when the string of pendulum makes an angle of 600 with vertical.
View SolutionA simple pendulum is constructed by attaching a bob of mas m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View Solution
Knowledge Check
A particle of mass m is attached to a string of length L and given velocity √10hL in the horizontal direction at the lowest point. Find tension in the string when the particle is at (a) (i) lowest position (ii) highest position, (b) when the string makes an angle 60∘ with (i) lower vertical and (ii) upper vertical.
A11mg , 5 mg , 9.5mg , 6.5 mgB10mg , 5 mg , 9.5mg , 6.5 mgC11mg , 5 mg , 9mg , 6.5 mgD11mg , 5 mg , 9.5mg , 6 mgA particle of mass m is tied to a light string of length l and rotated along a vertical circular path. What should be the minimum speed at the highest point of its path so that the string does not become slack at any position ?
A√2glB√glCzeroD√gl/2A body of mass m is tied to a string of length l and whirled in a verticle cirlce. The velocity of the body at the lowest position is u. Then the tension in the string at a position when the string makes an angle θ with the vertical is
Amu2lBmu2l+mgcosθCmu2l+mg(2cosθ−3)Dmu2l+mg(3cosθ−2)
A rod of length 1.0m and mass 0.5kg fixed at ond is initially hanging vertical. The other end is now raised until it makes an angle 60∘ with the vertical. How much work is required?
View SolutionOne end of a string of length 1 m is tied to a body of mass 0.5 kg. It is whirled in a vertical circle with angular velocity 4 rad s−1. Find the tension in the string when the body is at the lower most point of its motion. (take, g = 10 ms−1)
View SolutionA particle of mass 150 g is attached to one end of a massless inextensible string It is made to describe a vertical circle of radius 1 m When the string is making an angle of 48.2∘ with the vertical , its instantaneous speed is 2m/s What is the tension in the string in this position ? Whould this particle be able to complete its circular path ? .
View SolutionA pendulum bob has a speed 3m/s while passing thorugh its lowest position. What is its speed when it makes an angle of 600 with the vertical? The length of the pendulum is 0.5m Take g=10ms2.
View SolutionOne end of a string of length 1.5 m is tied to a stone of mass 0.4 kg and the other end to a small pivot on a smooth vertical board. What is the minimum speed of the stone required at its lower most point so that the string does not slack at any point in its motion along the vertical circle ?
View Solution
