ABCD एक समांतर चतुर्भुज है। यदि , तो किसके बराबर है ?
Step by step video & image solution for ABCD एक समांतर चतुर्भुज है। यदि vec(AB) = vec(a), vec(BC) = vec(c ), तो vec(BD) किसके बराबर है ? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
समीकरण x2+2x−143=0 के मुलो के वर्गो का योग क्या है ?
04:35View Solutionनिम्नलिखित में से कौन-सा एक, रिक्त समुच्चय है ?
02:48View SolutionABCD is a parallelogram Fig. 2 (c ) .64. ACand(BD)areitsdiagonals.Showtˆ<br> (a) vec (AC) +vec (BD) =2 vec (BC)<br>(b)vec (AC) - vec (BD) =2 vec (AB)
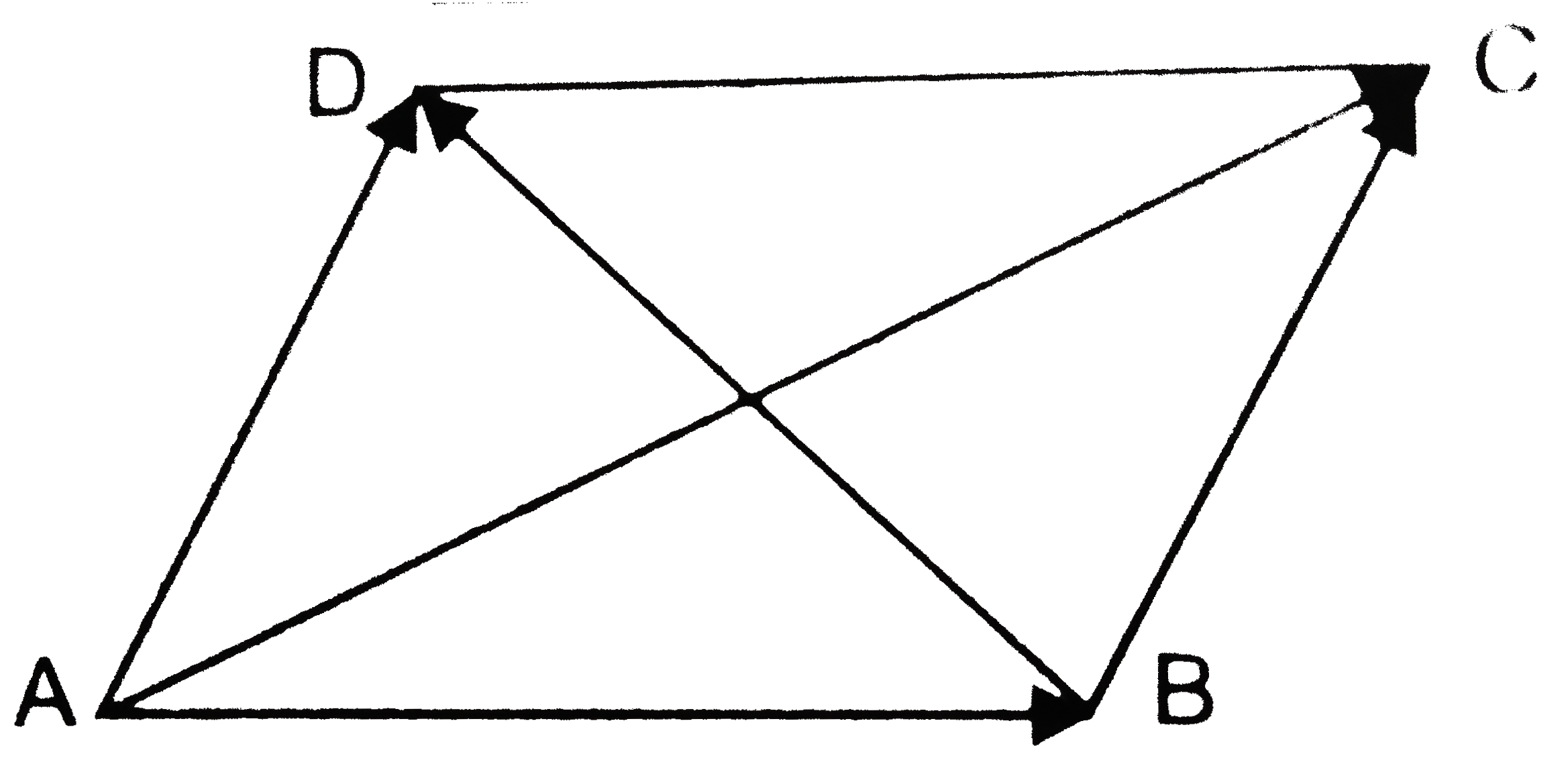. 02:39View SolutionA parallelogram ABCD. Prove that −−→AC+−−→BD=2−−→BC'
04:18View SolutionABCDE एक पंचभुज है तो −−→AB+−−→AE+−−→BC+−−→DC+−−→ED+−−→AD का मान होगा-
09:05View SolutionABCD is a parallelogram . If −−→AB=→a,−−→BC=→b, then what −−→BD equal to ?
03:34View SolutionABCD एक समांतर चतुर्भुज है ।AC और BD इसके विकर्ण है । सिद्ध कीजिए -
−−→AC+−−→BD=2−−→BC
−−→AC−−−→BD=2−−→AB.06:41View Solutionसमान्तर चतुर्भुज ABCD में, माना −−→AB = →a और −−→BC = →b, दिखाइए विकर्ण −−→AC=→a+→b और −−→BD=→b−→a.
04:11View SolutionABCD एक समान्तर चतुर्भुज हैं और AC, BD इसके विकर्ण हैं|
(a) −−→AB को −−→AC और −−→BD के रूप में व्यक्त करें| (b) −−→AC को −−→BD के रूप में व्यक्त करें|
साथ ही यह सिद्ध करें कि −−→AC+−−→BD=2−−→BC,−−→AC−−−→BD=2−−→AB02:48View SolutionABCDE एक समपंचभुज है। O इसका केंद्र है। सिद्ध कीजिए कि −−→OA+−−→OB+−−→OC+−−→OD+−−→OE=→0
01:46View Solutionकिसी समांतर चतुर्भुज ABCD में यदि −−→AB=¯a तथा −−→BC=¯b तो सिद्ध कीजिए कि
−−→AC=¯a+¯b और −−→BD=¯b−¯a.02:35View Solutionयदि −−→BC=4→a−8→b तथा −−→AB=→a−2→b हो , तो निम्न में सही संबंध है -
03:30View Solutionयदि →a,→b,→c समतलीय हो , तो [→a→b→c]=………. होगा।
08:00View Solution¯¯¯¯¯¯AC and ¯¯¯¯¯¯BD are the diagonals of the parallelogram ABCD. Prove that,
−−→AC+−−→BD=2−−→BC and −−→AC−−−→BD=2−−→AB04:05View SolutionIn a trapezium ABCD vec(AB)=3hati, vec(AD)=hati+2hatj ,vec(DC)=2hati . Find vec(BC),vec(BD),vec(AC) and angleBAD .
03:47View SolutionABCD is a parallelogram and AC, BD are its diagonals. Show that :
−−→AC+−−→BD=2−−→BC,−−→AC−−−→BD=2−−→AB.04:03View Solution