Charge is uniformly distributed with density ρ in a cylindrical region of radius R and infinite length. The magnitude of electric field at distance R2 and 2R from the axis of the cylinder is E1 and E2 respectively. The ratio E1E2 is equal to ___________.
The correct Answer is:1
To solve the problem of finding the ratio (E1)/(E2) for the electric field at distances (R/2) and 2R from the axis of a uniformly charged infinite cylinder, we can use Gauss's law. Here's a step-by-step solution:
Step 1: Understanding the Problem
We have a uniformly charged infinite cylinder with charge density ρ and radius R. We need to find the electric field at two different distances from the axis of the cylinder: E1 at r=R/2 and E2 at r=2R.
Step 2: Applying Gauss's Law
Gauss's law states that the electric flux through a closed surface is equal to the charge enclosed divided by the permittivity of free space (ϵ0):
ΦE=Qencϵ0
Where ΦE=∮→E⋅d→A.
Step 3: Finding E1 at r=R/2
1. Choose a Gaussian surface: A cylindrical surface of radius R/2 and length L.
2. Calculate the enclosed charge: The volume of the cylinder of radius R/2 and length L is:
V=π(R2)2L=πR2L4
The enclosed charge Qenc is:
Qenc=ρ⋅V=ρ⋅πR2L4
3. Calculate the electric field: The electric field E1 is uniform over the curved surface of the cylinder:
ΦE=E1⋅(2π⋅R2⋅L)=E1⋅πRL
Setting the two expressions for flux equal gives:
E1⋅πRL=ρ⋅πR2L4ϵ0
Simplifying:
E1=ρR4ϵ0
Step 4: Finding E2 at r=2R
1. Choose a Gaussian surface: A cylindrical surface of radius 2R and length L.
2. Calculate the enclosed charge: The entire charge within the cylinder of radius R is:
Qenc=ρ⋅πR2L
3. Calculate the electric field: The electric field E2 is uniform over the curved surface:
ΦE=E2⋅(2π⋅2R⋅L)=E2⋅4πRL
Setting the two expressions for flux equal gives:
E2⋅4πRL=ρ⋅πR2Lϵ0
Simplifying:
E2=ρR4ϵ0
Step 5: Finding the Ratio (E1)/(E2)
Now we can find the ratio:
E1E2=ρR4ϵ0ρR4ϵ0=1
Final Answer
The ratio E1E2 is equal to 1.
We have a uniformly charged infinite cylinder with charge density ρ and radius R. We need to find the electric field at two different distances from the axis of the cylinder: E1 at r=R/2 and E2 at r=2R.
Gauss's law states that the electric flux through a closed surface is equal to the charge enclosed divided by the permittivity of free space (ϵ0):
ΦE=Qencϵ0
Where ΦE=∮→E⋅d→A.
1. Choose a Gaussian surface: A cylindrical surface of radius R/2 and length L.
2. Calculate the enclosed charge: The volume of the cylinder of radius R/2 and length L is:
V=π(R2)2L=πR2L4
The enclosed charge Qenc is:
Qenc=ρ⋅V=ρ⋅πR2L4
3. Calculate the electric field: The electric field E1 is uniform over the curved surface of the cylinder:
ΦE=E1⋅(2π⋅R2⋅L)=E1⋅πRL
Setting the two expressions for flux equal gives:
E1⋅πRL=ρ⋅πR2L4ϵ0
Simplifying:
E1=ρR4ϵ0
1. Choose a Gaussian surface: A cylindrical surface of radius 2R and length L.
2. Calculate the enclosed charge: The entire charge within the cylinder of radius R is:
Qenc=ρ⋅πR2L
3. Calculate the electric field: The electric field E2 is uniform over the curved surface:
ΦE=E2⋅(2π⋅2R⋅L)=E2⋅4πRL
Setting the two expressions for flux equal gives:
E2⋅4πRL=ρ⋅πR2Lϵ0
Simplifying:
E2=ρR4ϵ0
Now we can find the ratio:
E1E2=ρR4ϵ0ρR4ϵ0=1
The ratio E1E2 is equal to 1.
Similar Questions
Consider a cylindrical surface of radius R and length l in a uniform electric field E. Compute the electric flux if the axis of the cylinder is parallel to the field direction.
View SolutionA cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
View Solution
Knowledge Check
- Question 1 - Select One
The magnitudes of the gravitational field at distance r1 and r2 from the centre of a uniform sphere of radius R and mass M are E1 and E2 respectively. Then:
AE1E2=r1r2 ir r1<R and r2<RBE1E2=r22r21 if r1<R and r2<RCE1E2=r31r32 if r1<R and r2<RDE1E2=r21r22 ir r1<R and r2<R - Question 2 - Select One
The magnitudes of the gravitational field at distance r1 and r2 from the centre of a uniform sphere of radius R and mass M are E1 and E2 respectively. Then:
AE1E2=r1r2 if r1<R and r2<RBE1E2=r22r21 if r1<R and r2<RCE1E2=r22r32 if r1<R and r2<RDE1E2=r21r22 if r1<R and r2<R - Question 3 - Select One
A time varying magnetic field B=Kr3t is existing in a cylindrical region of radius 'R' as shown (where k is a constant). The induced electric field 'E' at rR2 is
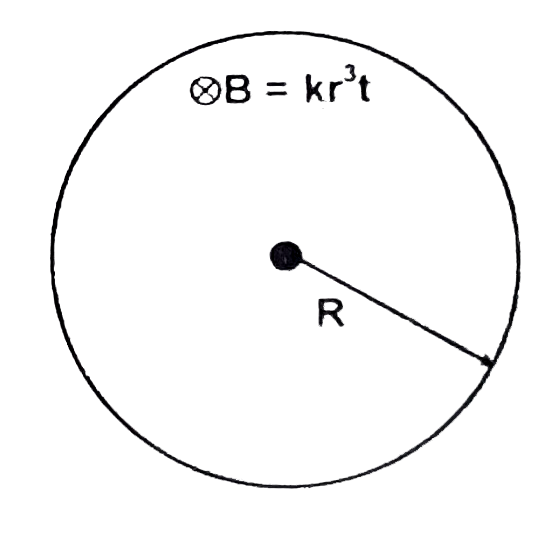 AKR420BKR440CKR460DKR480
AKR420BKR440CKR460DKR480
A cylinder of radius R and length L is placed in a uniform electric field E parallel to the axis. The total flux for the surface of the cylinder is given by
View SolutionCharges Q,2Q and 4Q are uniformly distributed in three solid spheres 1,2 and 3 of radii R/2. R and 2R respectively, as shown in Fig.If magnitude of the electric fields at point P at a distance R from the centre of sphere 1,2 and 3are E1,E2 and E3 respectively, then
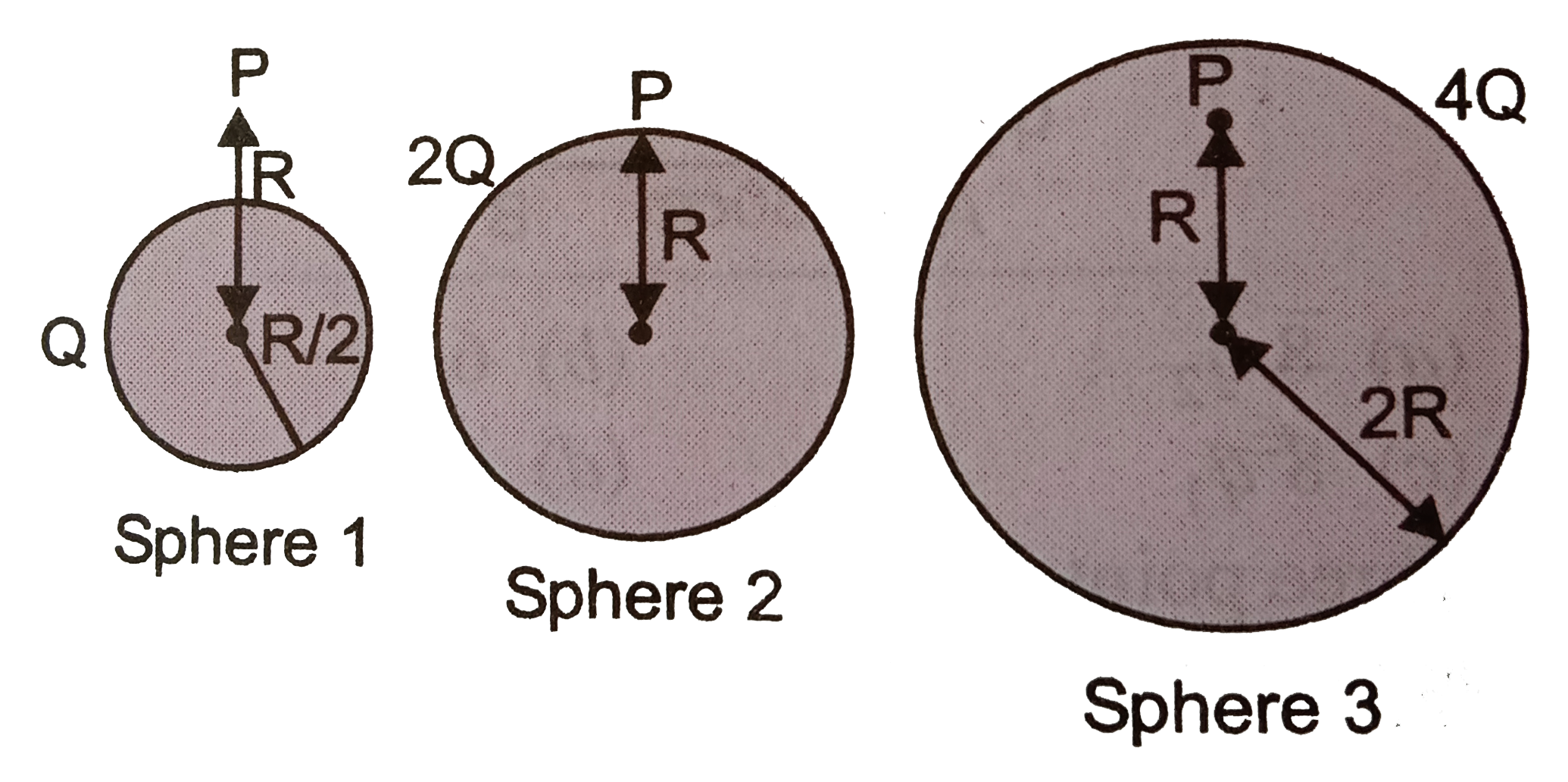 View Solution
View SolutionConsider a sphere of radius R and cylinder of length L. If both have same charge density σ and EsandEc are electric intensity at a point at a distance r from axis of sphere and cylinder respectively, then Es equal to
View SolutionThe electric field at a distance 3R2 from the centre of a charged conducting spherical shell of radius R is E. The electric field at a distance R2 from the centre of the sphere is :
View SolutionThe electric field at a distance 3R/2 from the centre of a charge conducting spherical shell of radius R is E. The electric field at a distance R/2 from the centre of the sphere is
View Solution

