एक बिंदु आवेश Q एक एकसमान रेखाइये आवेश घनत्व λ वाले अनंत लम्बाई के तार तथा एक एकसमान षेरेस्ट आवेश घनत्व σ वाले अन्ननत समतल चादर के कारण r दुरी पर विधुत क्षेत्र की त्रिवताये क्रमश E1(r),E2(r) तथा E3(r) है यदि एक दी गयी दुरी r0 पर E1(r0)=E2(r0)=E3(r0) तब
Q=4σπr20
r0=λ2πσ
E1(r0/2)=2E2(r0/2)
E2(r0/2)=4E3(r0/2)
The correct Answer is:C
Q4πε0r20=λ2πε0r0=σ2ε0
Q=2πσr20 विकल्प a सही नहीं है
λ2πε0r0=σ2ε0 अथवा r0=λπσ
विकल्प b सही नहीं है
E1(r0)=Q4πε0r20
E1(r0/2)=4Q4πε0r20=4E1(r0)
E2(r0/2)=2λ2πεr0=2E2(r0)
∴E1(r0/2)=2E2(r0/2) विकल्प c सही नहीं है
E3E0=E3(r0/2)=σ2ε0
∴E2(r0/2)=2E3(r0/2) विकल d सही नहीं है
Topper's Solved these Questions
- वैधुत फ्लेक्स तथा गौस की प्रमेय BOOK - NOOTAN HINDICHAPTER - वैधुत फ्लेक्स तथा गौस की प्रमेय EXERCISE - आंकिक
16 Videos
- वैधुत चालनBOOK - NOOTAN HINDICHAPTER - वैधुत चालनEXERCISE - वस्तुनिष्ठ प्रकार प्रश्न (एकल उत्तर प्रकार )
24 Videos
- वैधुत विभव BOOK - NOOTAN HINDICHAPTER - वैधुत विभव EXERCISE - विविध प्रतियोगी परीक्षाओ के लिए (वस्तुनिष्ठ प्रकार प्रश्न एकल उत्तर प्रकार)
17 Videos
Similar Questions
एक आवेश q एक घन के केंद्र पर स्थित है तो घन के किसी भी पृष्ठ से आने वाला वैधुत फ्लक्स होगा -
View Solutionएक राशि X , व्यंजक ε0LΔVΔt द्वारा व्यक्त की जाती है , जहाँ ε0 निर्वात की विधुतशीलता है , L लम्बाई है , ΔV विभवान्तर है तथा Δ समयान्तराल है । X का विमीय सूत्र वही है , जो कि है :
View Solutionएक आवेश Q लम्बाई L की छड़ AB के अनुदिश एकसमान रूप से वितरित है जैसा कि चित्र में दिखाया गया है । एक बिंदु O पर जो सिरे A से L दूरी पर है , वैधुत विभव है :

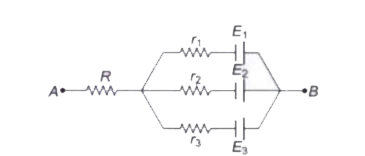
View SolutionIn the network shown the potential difference between A and B is (R = r_(1) = r_(2) = r_(3) = 1 Omega, E_(1) = 3V, E_(2) = 2V, E_(3) = 1V )
View SolutionIn the circuit shown here, E_(1) = E_(2) = E_(3) = 2 V and R_(1) = R_(2) = 4 ohms . The current flowing between point A and B through battery E_(2) is
View SolutionIn the circuit as shown in figure, E_(1)=2V , E_(2)=2V, E_(3)=1V, and R=r_(1)=r_(2)=r_(3)Omega . The potential difference between points A and B will be
View SolutionIn the following circuit E_(1)=E_(2)=E_(3) 2V and R_(1)=R_(2)=AOmega . The current passing through battery E_(2) between points A and B is
View SolutionIn the network shown the potential difference between A and B is R(=r_(1)=r_(2)=r_(3)=1Omega,E_(1)=3V,E_(2)=2V,E_(3)=1V)
View Solutionचित्र में प्रदर्शित में E1=3 वोल्ट, E3=2 वोल्ट, E3=1 वोल्ट तथा R=r1=r2=r3=1Ω
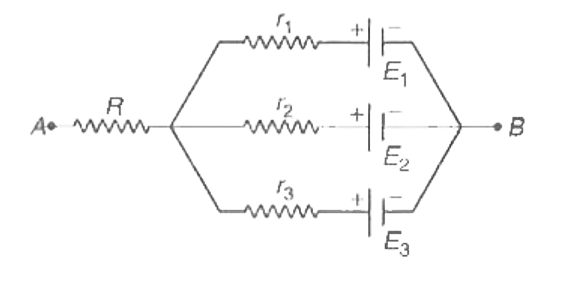
(a) A व B के बीच विभवांतर तथा प्रतयेक शाखा में धारा के मान की गड़ना कीजिए|
(b) यदि r2 को लघुपतित कर दे तथा A को B से जोड़ दे, तो E1,E2,E3 तथा R में प्रवाहित धारा का मान ज्ञात कीजिए|
View SolutionIf E_(1) , E_(2),E_(3) ... E_(n) represent emfs of a number of cells of internal resistances r_(1) , r_(2) , ... r_(n) then mention their equivalent emf and internal resistance when these are connected in series.
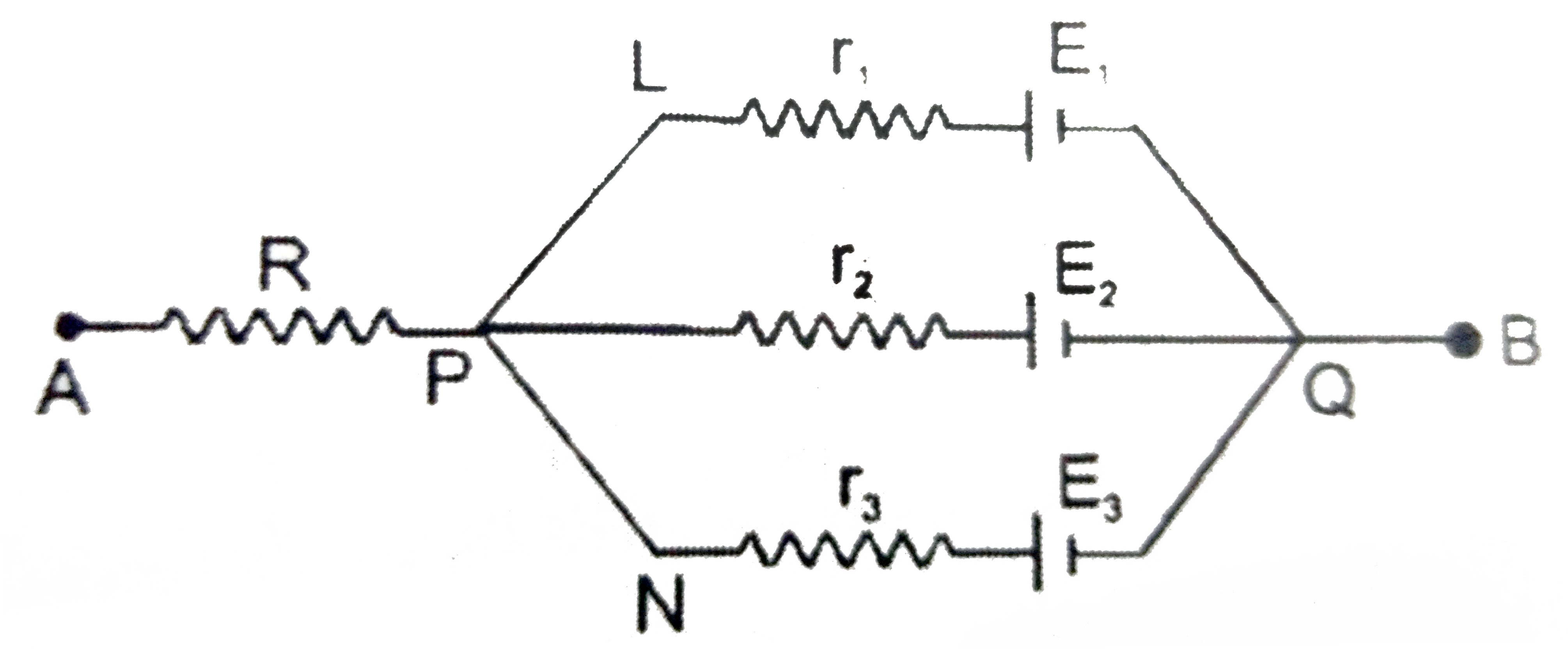
View SolutionIn the circuit shown in fig. E1=3 volt,E2=2 volt,E3=1 vole and R=r1=r2=r3=1ohm.
(i) Find potential difference in Volt between the points A and B with A & B unconnected.
(ii) If r2 is short circuited and the point A is coneted to point B through a zero resistance wire, find the current through R in ampere.
View SolutionTwo cells of emf E_(1) and E_(2) are joined in opposition ( such that E_(1) gt E_(2) ). If r_(1) and r_(2) be the internal resistance and R be the external resistance , then the terminal potential difference is
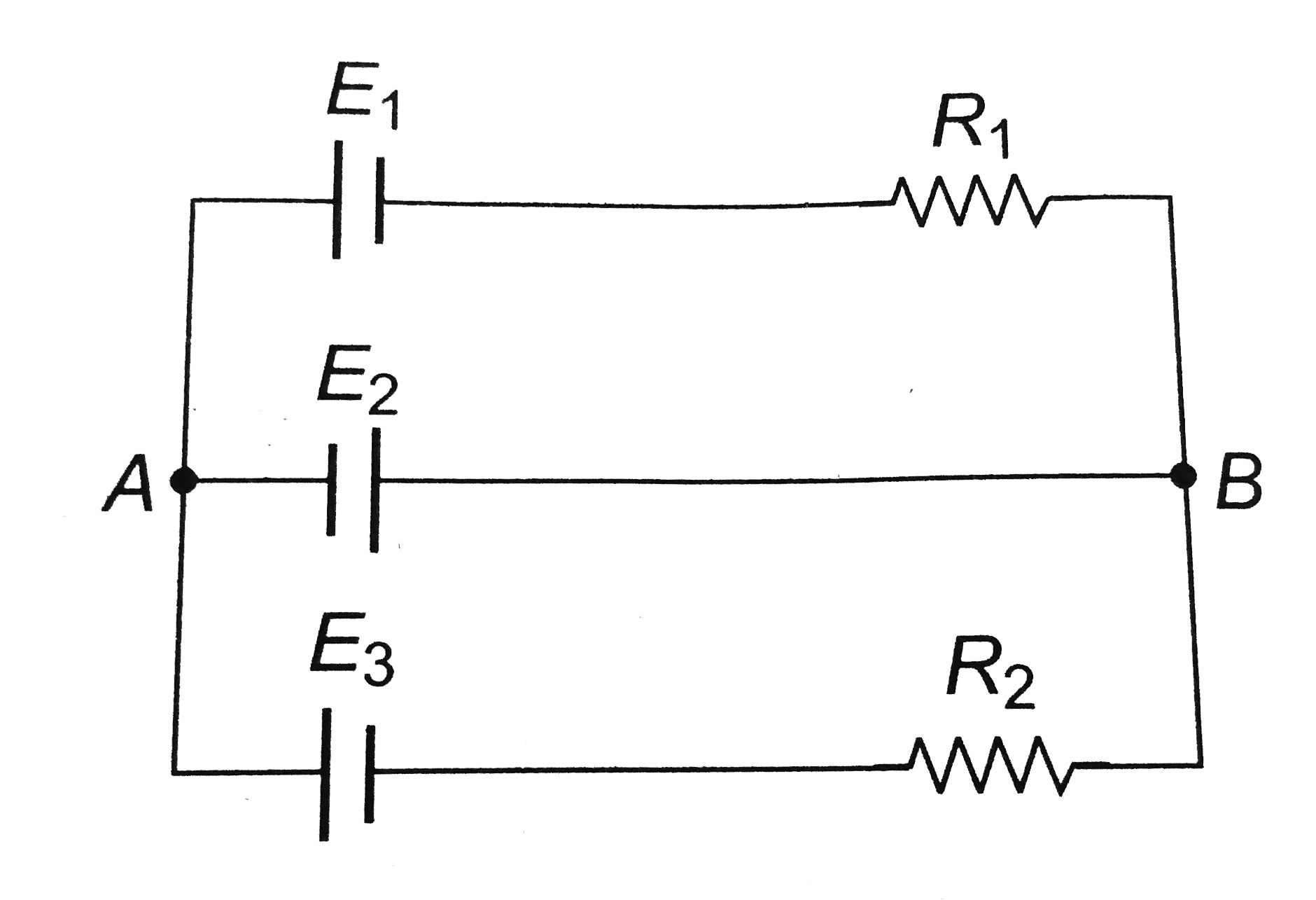
View SolutionIn the circuit shown here, E_(1) = E_(2) = E_(3) = 2 V and R_(1) = R_(2) = 4 ohms . The current flowing between point A and B through battery E_(2) is
View SolutionIn the circuit shown here, E1=E2=E3=2V and R1=R2=4ohms. The current flowing between point A and B through battery E2 is
View SolutionIn the network shown the potential difference between A and B is (R=r1=r2=r3=1Ω,E1=3V,E2=2V,E3=1V)
View Solution
