Find the resistance when the various resistor are connected in
parallel

Text Solution

Verified by Experts

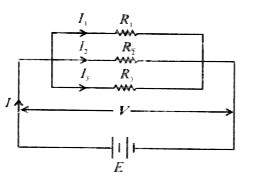
Resistors in parallel : Resistors are said to be connected in parallel if potential difference across them is same. Consider three resistors having resistances $R_{1}, R_{2} and R_{3}$ connected as shown in the figure. Let V be the potential difference applied across the combination with the help of a battery E. Let $I$ be the main current in the circuit. Let $I_{1}, I_{2} and I_{3}$ be the currents through resistance $R_{1}, R_{2} and R_{3}$ . respectively.
$I = I_{1} + I_{2} + I_{3} ... ... ... . (i)$
Potential difference across each resistor
$V = I_{1} R_{1} = I_{2} R_{2} = I_{3} R_{3}$
$\Rightarrow I - 1 = \frac{V}{R_{1}}, I_{2} = \frac{V}{R_{2}}, I_{3} = \frac{V}{R_{3}}$
Let R be the equivalent resistance of the circuit.
Then $V = I R \Rightarrow I = \frac{V}{R}$
Putting these values in equation (i), we get
$\frac{V}{R} = \frac{V}{R_{1}} + \frac{V}{R_{2}} + \frac{V}{R_{3}}$
$\Rightarrow \frac{1}{R} = \frac{1}{R_{1}} + \frac{1}{R_{2}} + \frac{1}{R_{3}} ... . (i i)$

Updated on:21/07/2023

The equivalent resistance of n identical resistors connected in parallel is x. If the resistors are connected in series, the equivalent resistance would be
An x
B $n^{2} x$
Cx/n
D $x / n^{2}$
The equivalent resistance of $n$ identical resistors connected in parallel si $x$ . If the resistors are connected in series, the equivalent resistance would be.
An x
B $n^{2} x$
C $\frac{x}{n}$
D $\frac{n}{x}$