Two heating elements of resistances $R_{1} and R_{2}$ when operated at a constant supply of voltage V, consume power $P_{1} and P_{2}$ respectively. Deduce the expression for the power of their combination when they are, in turn, connected in (i) series and (ii) parallel across the same voltage supply.

Text Solution

Verified by Experts

Power consumed when heating elements are arranged in:
i) Series combination : Total resistance $R_{s} = R_{1} + R_{2}$ .

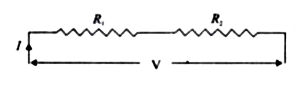
$∴$ Power consumed $= (P_{S}) = \frac{V^{2}}{R_{s}} = \frac{V^{2}}{(R_{1} + R_{2})} = I^{2} (R_{1} + R_{2}) [∵ I is same in series]$
$= I^{2} R_{1} + I^{2} R_{2} = P_{1} + P_{2}$
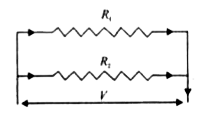
ii) Parallel combination:
In parallel combination $\frac{1}{R_{P}} = \frac{1}{R_{1}} + \frac{1}{R_{2}}$
$∴ R_{P} = \frac{R_{1} R_{2}}{R_{1} + R_{2}}$
Power consumed, $P_{P} = \frac{V^{2}}{R_{P}} = \frac{V^{2}}{\frac{R_{1} R_{2}}{R_{1} + R_{2}}} = \frac{V^{2} (R_{1} + R_{2})}{R_{1} R_{2}} [∵ V is same in parallel]$
$P_{P} = \frac{V^{2}}{R_{1}} + \frac{V^{2}}{R_{2}} = P_{1} + P_{2} ... ... ... . . (i i)$ .
Hence from (i) and (ii) it is clear that, the power consumed is same in series combination as well as in parallel combination.

Updated on:21/07/2023