A coil of resistance R and inductance L is connected across an a.c power supply of r.m.s. voltage V. The average power dissipated in the coil is,
V2/R
V2R(R2+ω2L2)
V2√R2+ω2L2
zero
The correct Answer is:B
To find the average power dissipated in a coil of resistance R and inductance L connected to an AC power supply with RMS voltage V, we can follow these steps:
1. Identify the Parameters:
- Resistance of the coil: R
- Inductance of the coil: L
- RMS Voltage across the coil: V
2. Understand the Concept of Impedance:
- The impedance Z of the coil in an AC circuit is given by:
Z=√R2+(ωL)2
where ω is the angular frequency of the AC supply.
3. Calculate the RMS Current:
- The RMS current I in the circuit can be expressed as:
I=VZ
- Substituting the expression for Z:
I=V√R2+(ωL)2
4. Use the Formula for Average Power:
- The average power Paverage dissipated in the coil can be calculated using the formula:
Paverage=I2R
- Substituting the expression for I:
Paverage=(V√R2+(ωL)2)2R
5. Simplify the Expression:
- Squaring the current expression:
Paverage=V2R2+(ωL)2R
- Thus, the final expression for the average power dissipated in the coil is:
Paverage=V2RR2+(ωL)2
Final Answer:
The average power dissipated in the coil is:
Paverage=V2RR2+(ωL)2
- Resistance of the coil: R
- Inductance of the coil: L
- RMS Voltage across the coil: V
- The impedance Z of the coil in an AC circuit is given by:
Z=√R2+(ωL)2
where ω is the angular frequency of the AC supply.
- The RMS current I in the circuit can be expressed as:
I=VZ
- Substituting the expression for Z:
I=V√R2+(ωL)2
- The average power Paverage dissipated in the coil can be calculated using the formula:
Paverage=I2R
- Substituting the expression for I:
Paverage=(V√R2+(ωL)2)2R
- Squaring the current expression:
Paverage=V2R2+(ωL)2R
- Thus, the final expression for the average power dissipated in the coil is:
Paverage=V2RR2+(ωL)2
The average power dissipated in the coil is:
Paverage=V2RR2+(ωL)2
Similar Questions
A choke coil of resistance R and inductance is connected to an ac. source of frequency f and peak voltage V If angular frequency will increase then, the average power dissipated in the choke
View SolutionA resistor of resistance R is connected to an ideal battery. If the value of R is decreased,the power dissipated in the resistor will
View SolutionA resistor of resistance R is connected to an ideal battery. If the value of R is decreased,the power dissipated in the resistor will
View SolutionIn an a.c. circuit consisting of resistance R and inductance L, the voltage across R is 60 volt and that across L is 80 volt.The total voltage across the combination is
View SolutionFigure below shows a capacitor C, an inductor L and a resistor R, connected in series to an a.c. supply of 220 V.
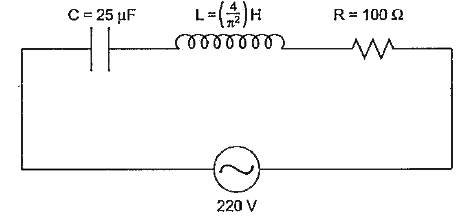
Average power consumed by the circuit.
View SolutionA coil of inductance 1H and neligible resistance is connected to a source of supply, whose voltage is given by V=4t VOLT. If the voltage is applied at t=0, find the energy stored in the coil in 4s
View SolutionA coil of resistance 40Ω is connected across a 4.0 V battery. 0.10 s after the battery is connected, the current in the coil is 63 mA. Find the inductance of the coil.
View SolutionIf a battery of emf E and internal resistance r is connected across a load of resistance R. Shot that the rate at which energy is dissipated in R is maximum when R=r and this maximur power is P=E2/4r.
View SolutionA capacitor of capacitance 2 mF and resistor of resistance 12 Ω are connected in series with voltage source V=(195√2(V))[sin(100rads)t] - The average power dissipated in the circuit will be
View SolutionAn inductor of inductance L and ressistor of resistance R are joined in series and connected by a source of frequency ω. Power dissipated in the circuit is
View Solution
