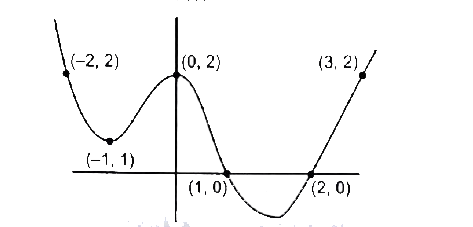
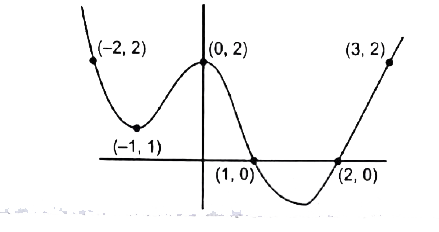
In the given figure graph of y=p(x)=x^(4)+ax^(3)+bx^(2)+cx+d is given

If $x^{2} + x + 1$ is a factor of $a x^{3} + b x^{2} + c x + d$ , then the real root of $a x^{3} + b x^{2} + c x + d = 0$ is
A $- d / a$
B $d / a$
C $a / d$
Dnone of these
If roots of the equation $x^{4} - 8 x^{3} + b x^{2} + c x + 16 = 0$ are positive, then
A $b = 8 = c$
B $b = - 24, c = - 32$
C $b = 24, c = - 32$
D $b = 24, c = 32$

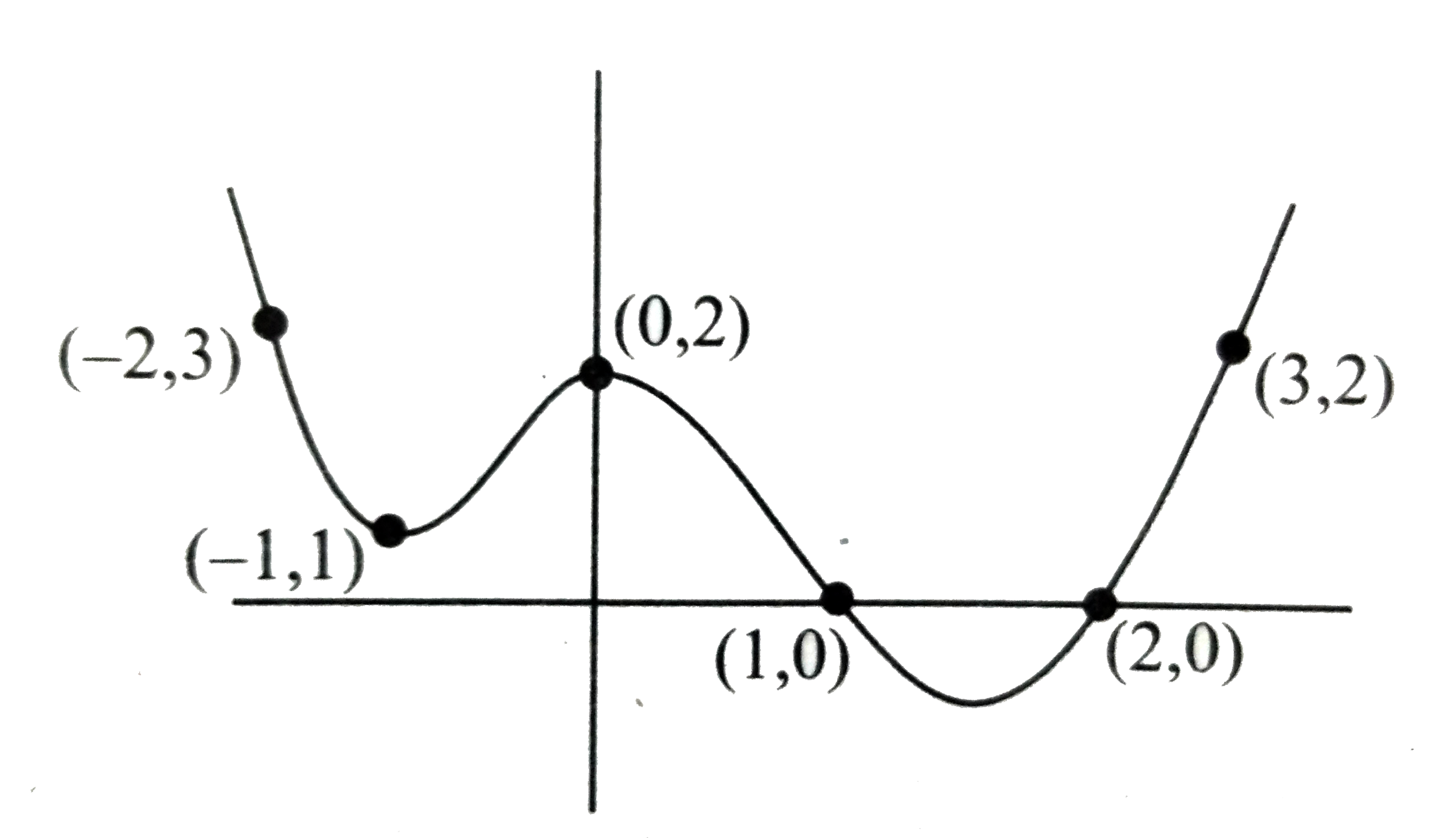
In the given figure graph of $y = p (x) = x^{4} + a x^{3} + b x^{2} + c x + d$ is given

The product of all imaginery roots of $p (x) = (0)$ is