The profit function, in rupees, of a firm selling t items (x≥0) per week is given by P(x)=−3500+(400−x)x. How many items should the firm sell so that the firm has maximum profit
400
30
200
200
The correct Answer is:C
To find the number of items the firm should sell to maximize profit, we will follow these steps:
Step 1: Write down the profit function
The profit function is given by:
P(x)=−3500+(400−x)x
Step 2: Simplify the profit function
We can expand the profit function:
P(x)=−3500+400x−x2
So, the profit function becomes:
P(x)=−x2+400x−3500
Step 3: Differentiate the profit function
To find the maximum profit, we need to differentiate P(x) with respect to x:
P′(x)=ddx(−x2+400x−3500)
Using the power rule, we get:
P′(x)=−2x+400
Step 4: Set the derivative equal to zero
To find the critical points, we set the derivative equal to zero:
−2x+400=0
Step 5: Solve for x
Now, we solve for x:
2x=400
x=200
Step 6: Conclusion
The firm should sell 200 items per week to maximize profit.
The profit function is given by:
P(x)=−3500+(400−x)x
We can expand the profit function:
P(x)=−3500+400x−x2
So, the profit function becomes:
P(x)=−x2+400x−3500
To find the maximum profit, we need to differentiate P(x) with respect to x:
P′(x)=ddx(−x2+400x−3500)
Using the power rule, we get:
P′(x)=−2x+400
To find the critical points, we set the derivative equal to zero:
−2x+400=0
Now, we solve for x:
2x=400
x=200
The firm should sell 200 items per week to maximize profit.
Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBOOK - PUNEET DOGRACHAPTER - APPLICATION OF DERIVATIVESEXERCISE - PREV YEAR QUESTIONS
85 Videos
- 3-D GEOMETRYBOOK - PUNEET DOGRACHAPTER - 3-D GEOMETRYEXERCISE - PREV YEAR QUESTIONS
108 Videos
- AREA BOUNDED BY CURVESBOOK - PUNEET DOGRACHAPTER - AREA BOUNDED BY CURVESEXERCISE - PREV YEAR QUESTIONS
39 Videos
Similar Questions
The profit function P(x) of a firm, selling x items per day is given by P(x)= (150−x)x−1625. Find the number of items the firm should manufacture to get maximum profit. Find the maximum profit
View SolutionA manufacturer can sell x items at the price of Rs. (330−x) each. The cost of producing xitems is Rs. x2+10x−12. How many items must be sold so that his profit is maximum?
View Solution
Knowledge Check
The profit fucntion in rupees of a firm selling x items (x≥0) per week is given by P(x)=−3500+(400−x)x How many items should the firm sell so that the firm has maximum profit ?
A400B300C200D100A person sold 25 articles for Rs.2500 and incurred a loss of 10%. How many articles should he sell for Rs2400 to make a profit of 20%?
एक व्यक्ति ने 2500 रुपये में 25 वस्तुएँ बेची और उसे 10% की हानि हुई | उसे 2400 रुपये में कितनी वस्तुएँ बेचनी चाहिए ताकि 20% का लाभ हो ?Ars 500Brs 640Crs 540Drs 600Manufacturer can sell x items at a price of rupees (5−x100)each. The cost price of x items is Rs (x5+500). Find the number of items he should sell to earn maximum profit
Ax=140Bx=240Cx=340Dx=440
A producer can sell any quantity of a commodity at a given price of Rs. 10 per unit. His cost schedule is given below:
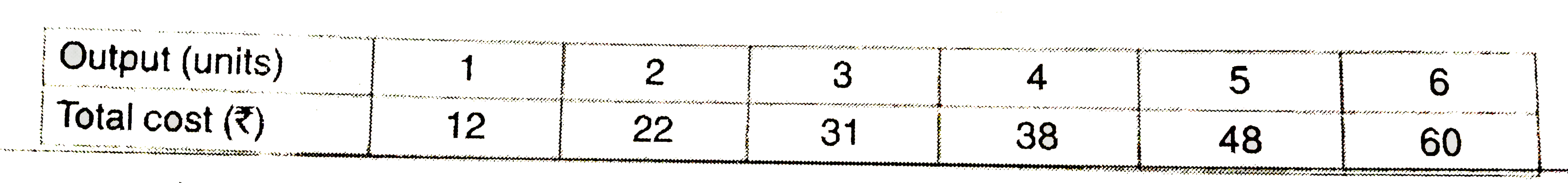
How many units should he produce to get maximum profit ? Explain.
View SolutionA manufacturer can sell x items at a price of Rs. (5−x100) each. The cost price of x items is Rs. (x5+ 500). Find the number of items he should sell to earn maximum profit.
View SolutionA manufacturer can sell 'x' items at a price of Rs (250−x) each. The cost of producing 'x' items is Rs (x2−50x+12). Determine the number of items to be sold so that he can make maximum profit.
View Solution(Manufacturing problem) A manufacturer has three machines I, II and III installed in his factory. Machines I and II are capable of being operated for at most 12 hours whereas machine HI must be operated for atleast 5 hours a day. She produces only two items M and N each requiring the use of all the three machines. The number of hours required for producing 1 unit of each of M and N on the three machines are given m the following table:She makes a profit of Rs 600 and Rs 400 on items M and N respectively. How many of each item should she produce so as to maximise her profit assuming that she can sell all the items that she produced? What will be the maximum profit?
View SolutionA manufacturer can sell x items per month at a price p= Rs.(300-2x) Manufacturer's cost of production, Rs.y, of x items is given by y=2x+1000 . Find the number of items to be produced per month to yield the maximum profit.
View Solution
