ABC is a right-angled triangle with AB = 6 cm and BC = 8 cm. A circle with centre O has been in scribed inside ΔABC. The radius of the circle is
1 cm
2 cm
3 cm
4 cm
The correct Answer is:B
To find the radius of the inscribed circle (inradius) of triangle ABC, we can follow these steps:
Step 1: Identify the sides of the triangle
Given:
- AB = 6 cm (one leg of the triangle)
- BC = 8 cm (the other leg of the triangle)
Since ABC is a right-angled triangle, we can use the Pythagorean theorem to find the length of the hypotenuse AC.
Step 2: Calculate the length of the hypotenuse AC
Using the Pythagorean theorem:
AC=√AB2+BC2=√62+82=√36+64=√100=10 cm
Step 3: Calculate the semi-perimeter (s) of triangle ABC
The semi-perimeter s is given by:
s=AB+BC+AC2=6+8+102=242=12 cm
Step 4: Calculate the area (A) of triangle ABC
The area A of a right-angled triangle can be calculated using:
A=12×AB×BC=12×6×8=24 cm2
Step 5: Calculate the radius (r) of the inscribed circle
The radius r of the inscribed circle can be found using the formula:
r=As=2412=2 cm
Final Answer
The radius of the inscribed circle in triangle ABC is 2 cm.
---
Given:
- AB = 6 cm (one leg of the triangle)
- BC = 8 cm (the other leg of the triangle)
Using the Pythagorean theorem:
AC=√AB2+BC2=√62+82=√36+64=√100=10 cm
The semi-perimeter s is given by:
s=AB+BC+AC2=6+8+102=242=12 cm
The area A of a right-angled triangle can be calculated using:
A=12×AB×BC=12×6×8=24 cm2
The radius r of the inscribed circle can be found using the formula:
r=As=2412=2 cm
The radius of the inscribed circle in triangle ABC is 2 cm.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-V)30videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-VI)8videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-III)109videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself10videos
DISCOUNT
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
Similar Questions
In the given figure ABC is a right angled triangle with AB=6 cm, and BC=8 cm. A circle with centre O has been inscribed inside the triangle. Find the radius of the circle.
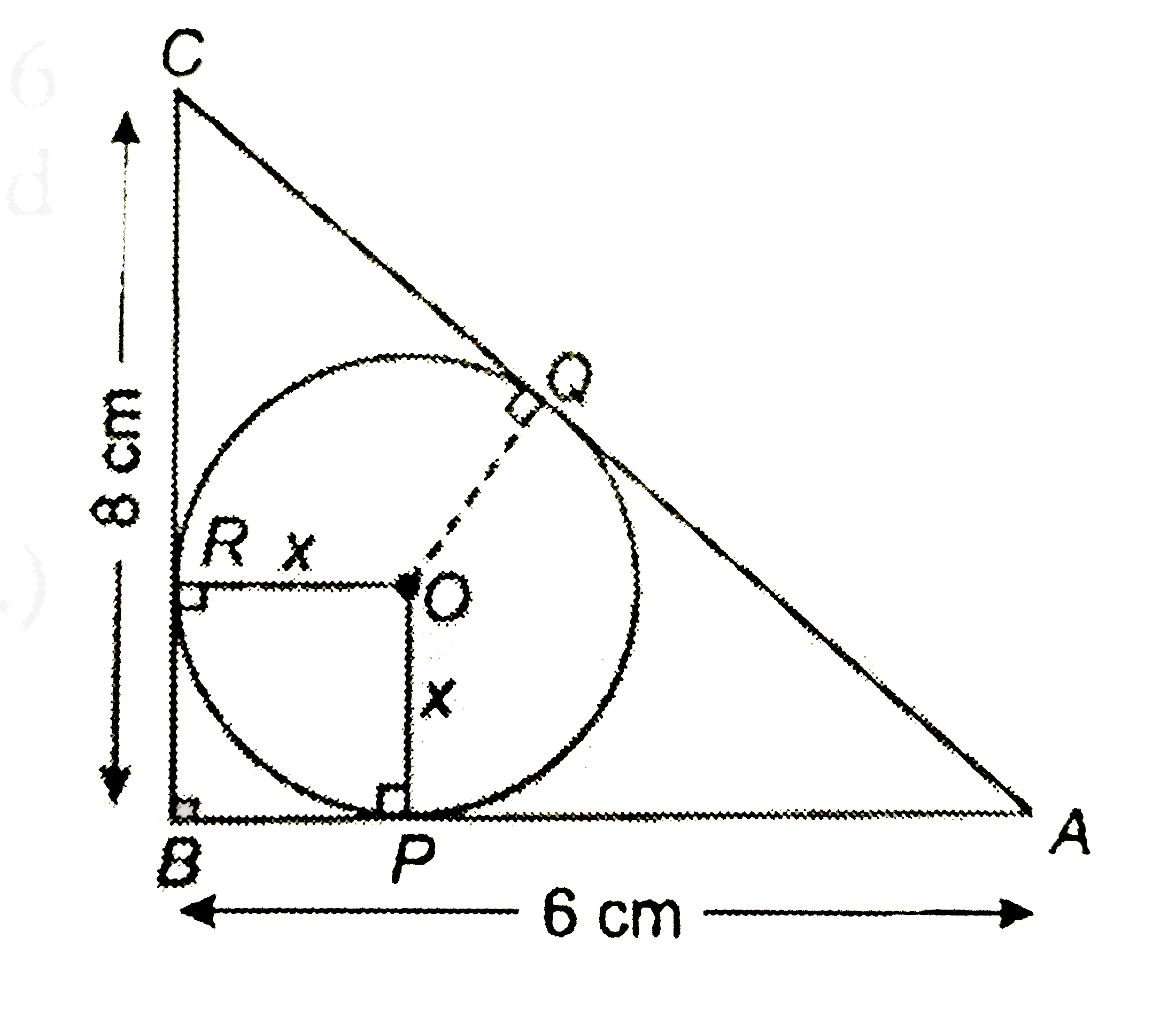 View Solution
View SolutionABC is a right angled triangle, right angled at B such that BC=6cm and AB=8cm . A circle with centre O is inscribed in ABC . The radius of the circle is (a) 1cm (b) 2cm (c) 3cm (d) 4cm
View Solution
Knowledge Check
- Question 1 - Select One
ABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :
 A1 cmB1.25 cmC1.5 cmDnone of these
A1 cmB1.25 cmC1.5 cmDnone of these - Question 2 - Select One
ABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :
A1 cmB1.25 cmC1.5 cmD2 cm - Question 3 - Select One
ABC is triangle right angled at B. If AB = 6 cm and BC= 8 cm, then what is the length of the circum- radius of the ΔABC ?
A10 cmB7 cmC6 cmD5 cm
In the given figure ΔABC is right angle at A with AB=6 cm and AC=8 cm. A circle with centre O has been inscribed inside the triangle. Find the value of r, the radius of the inscribed circle.
 View Solution
View SolutionPQR is a right angled triangle at Q with QR =12 a=cm and PQ=5cm. A circle with centre O is inscribed in △PQR. Find the radius of the circle.
View SolutionΔABC is a right angled triangle with ∠A=900AB=bcm,AC=acm,andBC=ccmAcircle is inscribed in this triangle. The radius of the circle,in cm, is:
View SolutionIn triangle ABC,right angled at B, BC = 24 cm, and AB = 7 cm. A circle is inscribed in triangle ABC. Then the radius of the circle is:
View SolutionABC is a right angled triangle AB = 3 cm, BC = 5 cm and AC = 4 cm, then the inradius of the circle is :
 View Solution
View Solution

