Question

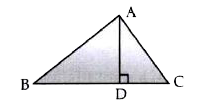
In $\Delta ABC,A{D}_I\_BC\text{and}A{D}^2=BD,DC$. The measure of $\angle BAC$ is:

Options

A. `60^@`
B. `75^@`
C. `90^@`
D. `45^@`

Answer

C

Explanation

To solve the problem, we need to analyze the given information about triangle ABC and the relationship between its segments.

Step 1: Understand the triangle and the given information.
- We have triangle ABC where AD is perpendicular to BC. This means that angle ADB and angle ADC are both right angles (90 degrees).

Step 2: Use the given relationship.
- We are given that \( AD^2 = BD \cdot DC \). This is a property of right triangles, specifically related to the altitude drawn from the right angle to the hypotenuse.

Step 3: Apply the property of right triangles.
- In any right triangle, if an altitude is drawn from the right angle to the hypotenuse, the square of the length of the altitude (AD) is equal to the product of the lengths of the two segments of the hypotenuse (BD and DC). This confirms that triangle ABC is indeed a right triangle.

Step 4: Determine the measure of angle BAC.
- Since AD is perpendicular to BC, angle BAC is the angle opposite to the side AD. In triangle ABC, since AD is the altitude, angle BAC must be 90 degrees.

Final Answer:
The measure of angle BAC is \( 90^\circ \).

---