In ΔABC the straight line parallel to the side BCmeets ABandACat the points PandQ respectively. If AP=QC, the length of ABis 12 units and the length of AQis 2 units, then the length (in units) of CQ is
4
6
8
10
The correct Answer is:A
To solve the problem, we will follow these steps:
Step 1: Understand the Given Information
We have triangle ABC with a line parallel to side BC, which intersects sides AB and AC at points P and Q respectively. We know:
- Length of AB = 12 units
- Length of AQ = 2 units
- AP = QC (let's denote this common length as X)
Step 2: Set Up the Ratios
According to the theorem related to parallel lines in triangles, the segments created by the intersection of a line parallel to one side of a triangle with the other two sides are proportional. Therefore, we can write the following ratio:
APPB=AQQC
Where:
- AP = X
- PB = AB - AP = 12 - X
- AQ = 2
- QC = X
Thus, we can express the ratio as:
X12−X=2X
Step 3: Cross Multiply to Solve for X
Cross-multiplying gives us:
X2=2(12−X)
Expanding this, we have:
X2=24−2X
Rearranging the equation results in:
X2+2X−24=0
Step 4: Factor the Quadratic Equation
We need to factor the quadratic equation X2+2X−24=0. We look for two numbers that multiply to -24 and add to 2. These numbers are 6 and -4.
Thus, we can factor the equation as:
(X+6)(X−4)=0
Step 5: Solve for X
Setting each factor to zero gives us:
1. X+6=0⇒X=−6 (not valid since length cannot be negative)
2. X−4=0⇒X=4
Step 6: Find the Length of CQ
Since we have established that QC=X, we find:
CQ=4 units
Final Answer
The length of CQ is 4 units.
---
We have triangle ABC with a line parallel to side BC, which intersects sides AB and AC at points P and Q respectively. We know:
- Length of AB = 12 units
- Length of AQ = 2 units
- AP = QC (let's denote this common length as X)
According to the theorem related to parallel lines in triangles, the segments created by the intersection of a line parallel to one side of a triangle with the other two sides are proportional. Therefore, we can write the following ratio:
- AP = X
- PB = AB - AP = 12 - X
- AQ = 2
- QC = X
Cross-multiplying gives us:
We need to factor the quadratic equation X2+2X−24=0. We look for two numbers that multiply to -24 and add to 2. These numbers are 6 and -4.
Setting each factor to zero gives us:
2. X−4=0⇒X=4
Since we have established that QC=X, we find:
The length of CQ is 4 units.
Topper's Solved these Questions
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-VI)8videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-VII)6videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE-IV)35videos
GEOMETRY
- BOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself10videos
DISCOUNT
- BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself18videos
LCM AND HCF
Similar Questions
ABC is a right triangle, right - angled at the vertex A. A circle is drawn to touch the sides AB and AC at points P and Q respectively such that the other end points of the diameters passing through P and Q lie on the side BC. IF AB = 6 units, then the area (in sq. units) of the circular sector which lies inside the triangle is
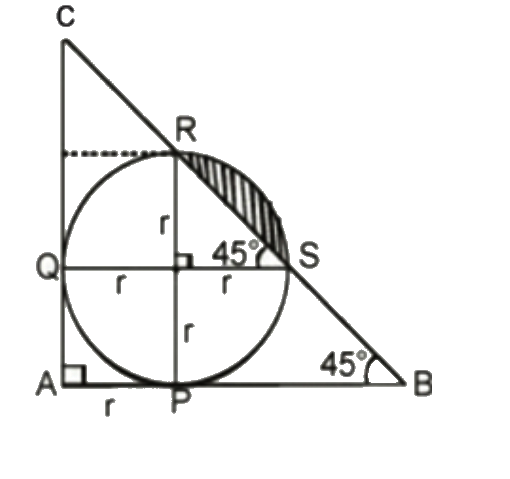 View Solution
View Solutionthe length of side AB and side BC a scalene triangle ABC are 12cm and 8cm respectively. the value of angle C is 59. find the length of side AC
View Solution
Knowledge Check
- Question 1 - Select One
Inside a triangle ABC, a straight line parallel to BC intersects AB and AC at the point P and respectively. If AB=3PB, then PQ:BC is
Aa) 1:3Bb) 3:4Cc) 1:2Dd) 2:3 - Question 2 - Select One
In ΔABC, the line parallel to BC Intersects AB and AC at P and Q respectively. If AB:AP=5:3then AQ:QCis :
A3:2B2:3C3:5D1:2 - Question 3 - Select One
A line parallel to side BC of ΔABC meets AB and AC respectively at P and Q. If AP=QC,PB=4 unit and AQ=9 unit, then length of AP is
A2.5 unitB3 unitC6 unitD6.5 unit
Length of two sides AB and BC of a triangle ABC are 28cm and 38 cm respectively . find the length of its third side AC if the perimeter of ABC is 100 cm
View SolutionThe mid points of the sides AB and AC of a triangle aBC are (2,−1) and (−4,7) respectively, then the length of BC is
View SolutionA circle touches the side BC of a ΔABC at P and also touches AB and AC produced at Q and R, respectively. If the perimeter of ΔABC = 26.4 cm, then the length of AQ is:
View SolutionIn figure , the sides AB, BC and CA of triangle ABC, touch a circle at P,Q and R, respectively . If PA = 4 cm , BP = 3 cm and AC = 11 cm , then length of BC is
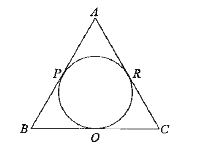 View Solution
View SolutionA circle is inscribed in a triangle ABC. It touches the sides AB, BC and AC at the points R, P and Q respectively. If AQ = 4.5 cm, PC = 5.5 cm and BR = 6 cm, then the perimeter of the triangle ABC is:
एक वृत्त किसी त्रिभुज ABC में अन्तर्निहित है | यह भुजाओं AB, BC और AC को क्रमशः बिंदु R, P और Q पर स्पर्श करता है | यदि AQ = 4.5 सेमी, PC = 5.5 सेमी और BR = 6 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |View Solution

