The feasible region for no. LPP is always a .......... polygon. Solution in Punjabi
The correct Answer is:Convex
Step by step video, text & image solution for The feasible region for no. LPP is always a .......... polygon. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR PROGRAMMING Book:ACCURATE PUBLICATIONChapter:LINEAR PROGRAMMING Exercise:QUESTIONS CARRYING 1 MARK (TYPE-III : TRUE OR FALSE QUESTIONS)
Explore 10 Videos
- LINEAR PROGRAMMING Book:ACCURATE PUBLICATIONChapter:LINEAR PROGRAMMING Exercise:QUESTIONS CARRYING 6 MARKS
Explore 7 Videos
- LINEAR PROGRAMMING Book:ACCURATE PUBLICATIONChapter:LINEAR PROGRAMMING Exercise:QUESTIONS CARRYING 1 MARK (TYPE-I : MULTIPLE CHOICE QUESTIONS)
Explore 15 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBook:ACCURATE PUBLICATIONChapter:INVERSE TRIGONOMETRIC FUNCTIONSExercise:QUESTIONS CARRYING 4 MARKS
Explore 27 Videos
- MATRICESBook:ACCURATE PUBLICATIONChapter:MATRICESExercise:QUESTIONS CARRYING 6 MARKS
Explore 4 Videos
Similar Questions
If the feasible region for a linear programming problem is bounded, then the objective function Z = ax+by has both a maximum and a minimum value on R.
View SolutionFind the maximum value of f = x+2 y subject to the constraints
2x+3y≤6
x+4y≤4
x,y≥0
View SolutionThe feasible solution for a LPP is shown in Fig. Let. Z = 3x - 4 y be the objective function. Minimum of Z occurs at
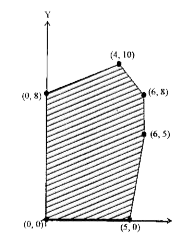
View SolutionWrite the value of tan−1[2sin(2cos−1√32)].
View SolutionIf A=⎡⎢⎣1−202130−21⎤⎥⎦,B=⎡⎢⎣72−6−21−3−425⎤⎥⎦ , find AB Also solve x−2y=10,2x+y+3z=8,−2y+z=7
View SolutionMaximum value of the objective function Z = ax +by in a LPP always occurs at only one corner point of the feasible region.
View SolutionIn a LPP, the maximum value of the objective function Z = ax +by is always 0, if origin is one of the corner point of the feasible region.
View SolutionConsider the following statements
I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
Which of the following statements are true?
View SolutionThe constraints of an LPP a 5≤x≤10,5≤y≤10 Determine the vertices of the feasible region formed by them
View SolutionDefine the term corner point of a feasible region in an LPP.
View SolutionMaximum value of the objective function Z = ax +by in a LPP always occurs at only one corner point of the feasible region.
View SolutionIn a LPP, the maximum value of the objective function Z = ax +by is always 0, if origin is one of the corner point of the feasible region.
View SolutionDefine Feasible region in LPP.
View SolutionThe feasible region for an LLP is always a …….. polygon.
View SolutionMaximum value of the objective function Z = ax + by in a LPP always occurs at only one corner point of the feasible region.
View SolutionIn a LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
View Solution