Derive the expression for the impedance of an a.c. circuit with LCR circuit in series.

Text Solution

Verified by Experts

Let a pure resistance R, a pure inductance L and ideal capacitor of capacitance C be connected in series to a source of alternating e.m.f. As RLC are in series. . Current at any instant through the three elements has the same amplitude and phase. Let it be represented by
$I = I_{0} sin ω t$
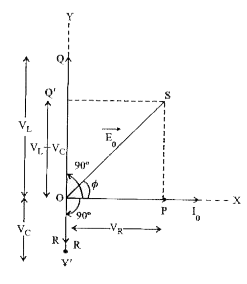
(i) The maximum voltage across R is $- \to V_{R} = \to I_{0} R$ . As $- \to V_{R}$ is in phase with current, it is represented by $- - \to O P$ along OX.
(ii) The maximum voltage across L is $- \to V_{L} = \to I_{0} X_{L}$ . As the voltage across the inductor leads the current by $90^{\circ}$ . It is represented by $- - \to O Q$ along $- - \to O Y$ .
(iii) The maximum voltage across C is $- \to V_{C} = \to I_{0} C$ . As voltage across capactor logs behind the alternating current by $90^{\circ}$ . It is represented $- - \to O R$ or along $- - \to O Y$ . As the $- \to V_{L}$ and $- \to V_{C}$ have phase difference of $180^{\circ}$ , net reactive voltage is $- \to V_{L} - - \to V_{C}$ is represented by $- - \to O Q$ .
The resultant of $- - \to O P$ and $- - \to O Q$ is the diagonal $- - \to O S$ .
$O S = \sqrt{{(O P)}^{2} + {(O Q .)}^{2}}$
$E_{0} = \sqrt{{(V_{R})}_{R}^{2} + {(V_{L} - V_{C})}_{L}^{2}}$
$E_{0} = \sqrt{{(I_{0} R)}_{0}^{2} + {(I_{0} X_{L} - I_{0} X_{C})}_{0}^{2}}$
$E_{0} = I_{0} \sqrt{{(R)}^{2} + {(X_{L} - X_{C})}_{L}^{2}}$
$E_{0} = I_{0} \sqrt{{(R)}^{2} + {(X_{L} - X_{C})}_{L}^{2}}$
$\frac{E_{0}}{I_{0}} = \sqrt{R^{2} + {(X_{L} - X_{C})}_{L}^{2}}$
$Z = \sqrt{R^{2} + {(X_{L} - X_{C})}_{L}^{2}}$
where, $Z = \frac{E_{0}}{I_{0}}$
where Z is called impedance of circuit.
It is clear that, in an AC circuit containig RLC the voltage leads the current by a phase angle $ϕ$ .
where $tan ϕ = \frac{P S}{O P}$
$tan ϕ = \frac{O Q .}{O P}$
$= \frac{V_{L} - V_{C}}{V_{R}}$
$= \frac{I_{0} X_{L} - I_{0} X_{C}}{I_{0} R}$
tan phi = (cancel(I_(0))(X_(L) - X_(L)))/(cancel(I_(0))R)
$tan ϕ = \frac{X_{L} - X_{C}}{R}$
Also $E = E_{0} sin (ω t + ϕ)$
Case I : When $X_{L}$ equal to $X_{C}$
$tan ϕ = 0$
i.e., $ϕ = 0$ hence voltage and current are in phase, then a.c. circuit is non inductive.
Case II : When $X_{L} > X_{C}$
$tan ϕ$ = is + ve, i.e, $ϕ$ is +ve. Hence voltage lead the current by a phase angle $ϕ$ .
The a.c. circuit is inductance dominated circuit.
Case III : When $X_{L} < X_{C}$
$tan ϕ$ - ve i.e., $ϕ$ is -ve
Hence voltage lags behind the current by a phase angle $ϕ$ . The a.c. circuit is called capacitance dominated circuit.

Updated on:21/07/2023

At resonance frequency the impedance in series LCR circuit is
Amaximum
Bminimum
Czero
Dinfinity
At resonance frequency the impedance in series LCR circuit is
Amaximum
Bminimum
Czero
Dinfinity
When the frequency of AC is doubled, the impedance of an LCR, circuit is
Ahalved
Bdoubled
Cincreases
Ddecreases