In fig., ABC is a quadrant of a circle of radius 14 cm and a semi circle is drawn with BC as diameter. Find the area of the shaded region.
 Solution in Punjabi
Solution in Punjabi
The correct Answer is:86cm2
Step by step video & image solution for In fig., ABC is a quadrant of a circle of radius 14 cm and a semi circle is drawn with BC as diameter. Find the area of the shaded region. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Find the area of sector of a circle with radius 6 cm, if angle of the sector is 60∘.
View SolutionWhich term of the A.P. 121, 117, 113, ... is its first negative term ?
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionFind the area of the shaded region, given that the radius of each circle is equal to 5 cm.
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionThe area of the shaded part in the figure given below is ______.

View SolutionThe inequation represented by the graph given below is :
View SolutionThe inequation that best describes the graph given below is _________
View SolutionThe inequation that best describes the following graph is _________
View SolutionWhich inequations represent the shaded region in the given figure
View SolutionIn fig. O is the center of the circle. Find the value of x.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_S01_031_Q01.png" width="80%"gt
View SolutionIn Fig, find the value of x.
ltimg src="https://d10lpgp6xz60nq.cloudfront.net/physics_images/PS_MATH_IX_C12_S01_032_Q01.png" width="80%"gt
View Solutionआकृति में, ABC, त्रिज्या 14 सेमी वाले एक वृत का चतुर्थाश है तथा BC को व्यास मान कर एक अर्धवृत्त खींचा गया है छायांकित भाग का क्षेत्रफल ज्ञात कीजिए -
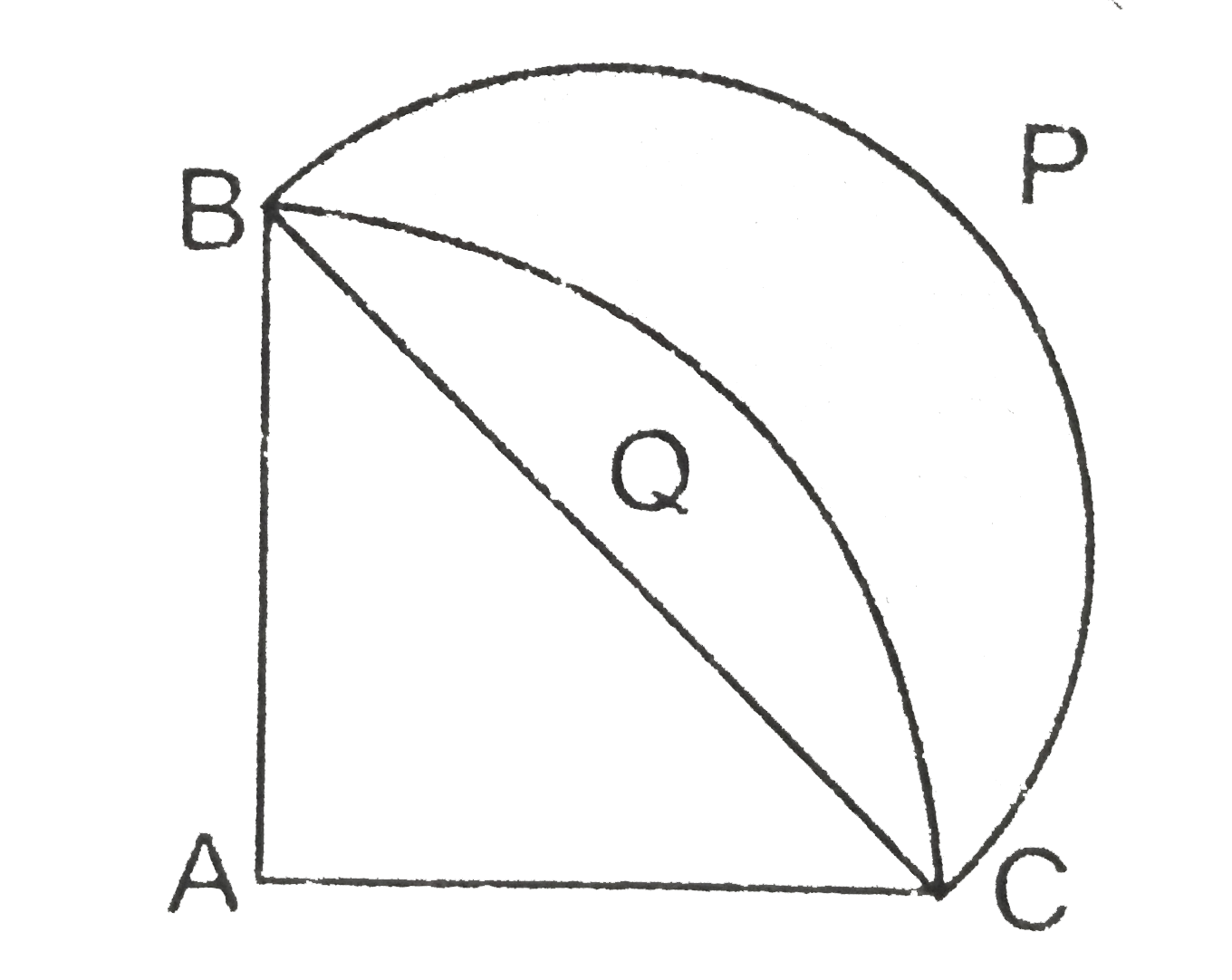
View SolutionIn Fig. 12.33, ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.
View Solution